Alternating Current Circuit Containing Inductance only (L-Circuit): Let us consider, An alternating current circuit containing a coil of inductance $L$ only. This inductor is connected with an alternating EMF i.e electromotive force source i.e.
$E=E_{\circ}sin\omega t\qquad(1)$
The current $i$ in coil varies continuously then an opposite emf is induced in the coil whose magnitude is $L\frac{di}{dt}$ So the net instantaneous of the circuit:
$E_{\circ}sin\omega t -L\frac{di}{dt}=0$
$E_{\circ}sin\omega t =L\frac{di}{dt}$
$di=\frac{E_{\circ}}{L}sin\omega dt$
Now integrate the above equation then the above equation can be written as
$\int di=\int \frac{E_{\circ}}{L}sin\omega dt$
$\int di= \frac{E_{\circ}}{L} \int sin\omega dt$
$i= \frac{E_{\circ}}{L} \frac{-cos\omega t}{\omega}$
$i= -\frac{E_{\circ}}{\omega L} cos\omega t$
$i= -\frac{E_{\circ}}{X_{L}} cos\omega t$
Where $X_{L}= \omega L$ is known as inductive reactance.
$i= -i_{\circ} cos\omega t$
Where $i_{\circ}=\frac{E_{\circ}}{X_{L}}$ is known as the maximum value of current in the circuit. Now compare this equation to Ohm's law then we find that the term $X_{L}=\omega L$ has the dimensions of resistance. It defines the 'effective opposition' of the coil to the flow of alternating current. it is known as the 'reactance of the coil' or 'inductive reactance' and it is denoted by $X_{L}$. The inductive reactance $X_{L}$ is zero for DC at which frequency is zero.
$i= -i_{\circ} sin \left(\frac{\pi}{2}- \omega t \right)$
$i= i_{\circ} sin \left(\omega t - \frac{\pi}{2} \right) \qquad(2)$
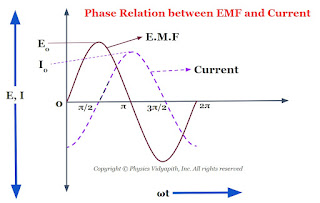
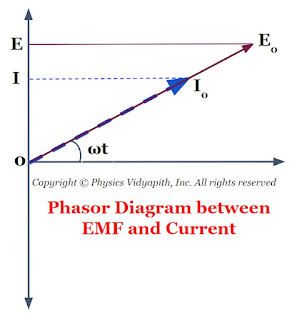
Now compare equation $(1)$ and equation $(2)$ which shows that an alternating circuit containing an inductor only, the current lags behind the emf by a phase angle of $\frac{\pi}{2}$ or $90^\circ$ (or the emf leads the current by a phase angle of $\frac{\pi}{2}$). The phase diagram between EMF and the current of an inductor is shown below-
The phasor diagram between the EMF and current of an inductor is also shown in the given figure below-
Electric field Intensity (Definition) and Electric field Intensity due to point charge
Definition of Electric Field Intensity:
Let us consider that a test-charged particle of $q_{0}$ Coulomb is placed at a point in the electric field and a force $F$ acting on them so the electric field intensity at that point
$ \overrightarrow{E}=\frac{\overrightarrow{F}}{q_{0}}$
SI Unit:$\quad Newton/Coulomb$ $ (N/C)$ $\quad Kg-m^{2}/sec^{3} A$
Dimension: $\left [ML^{2}T^{-3}A^{-1} \right ]$
Physical Significance of Electric Field:
The force experienced by a charge is different at different points in space. So electric field intensity also varies from point to point. In general, Electric field intensity is not a single vector quantity but it is a set of infinite vector and each point in space have a unique electric field intensity. So electric field is an example of the vector field.
Electric Field Intensity due to a Point Charge:
Let us consider that an isolated point charge of $+q$ Coulomb is placed at a point $O$ in a medium whose dielectric constant is $K$. If a test charge particle of $q_{0}$ Coulomb is placed at a point $P$ in the electric field at a distance $r$ from point $O$. So the electric field intensity (magnitude form) at point $P$
$E=\frac{F}{q_{0}}\qquad (1)$
According to Coulomb's Law:
$F=\frac{1}{4\pi \varepsilon _{0}K}\frac{qq_{0}}{r^{2}}\qquad (2)$
From equation $(1)$ and equation $(2)$, we can write
$E=\frac{1}{4\pi \varepsilon _{0}K}\frac{q}{r^{2}} \qquad (3)$
For air or vacuum $K=1$, Then from equation $(3)$
$E=\frac{1}{4\pi \varepsilon _{0}}\frac{q}{r^{2}} \qquad (4)$
Where
$\frac{1}{4\pi \varepsilon _{0}}=9\times10^{9} N-m^{2}/C^{2}$
From equation $(4)$
$E=9\times 10^{9} \frac{q}{r^{2}}\qquad (5)$
In Vector Notation:
$\overrightarrow{E}=\frac{1}{4\pi \varepsilon _{0}K}\frac{q}{r^{2}}r\hat{}$
If a system containing $'n'$ point charge $q_{1},q_{2},q_{3},..........q_{n}$ then electric field intensity due to the system of charge particle will be equal to the vector sum of the intensities i.e.
$\overrightarrow{E}=\overrightarrow{E_{1}}+\overrightarrow{E_{2}}+\overrightarrow{E_{3}}+....+\overrightarrow{E_{n}}$
$\overrightarrow{E}=\frac{1}{4\pi \varepsilon _{0}K}\sum_{i=0}^{n}\frac{q_{i}}{r_{i}^{2}}r_{i}\hat{}$
Where $r_{i}$ is the distance from point $'P'$ to charge $q_{i}$.
The force acting on the per unit test charge in electric field is called the Electric field intensity. It is represented by $'E'$.
 |
| Electric field intensity due to a point charge |
Refraction of light and its Properties
Definition of Refraction of light→
When a light goes from one medium to another medium then light bends from the path. This bending of the light phenomenon is knowns as the refraction of light.
When light goes from a rarer medium to a denser medium, light bends toward the normal as shown in the figure below:
When light goes from a denser medium to a rarer medium, the light goes away from normal as shown in the figure below.
Properties of refraction of light→
$\frac{sin \: i}{sin \: r}=constant(_{1}n_{2}) $
$\frac{sin \: i}{sin \: r}= (_{1}n_{2})$
$\frac{sin \: i}{sin \:r}=\frac{n_{2}}{n_{1}}$
Where $_{1}n_{2}$ is the refractive index of medium $(2)$ with respect to medium $(1)$ .
Absolute refractive index→
The ratio of the speed of light in a vacuum to the speed of light in a medium is called the absolute refractive index of the medium.
$refractive\: index(n)=\frac{speed\: of\:light\: in\: vacuum(c)}{speed \:of \:light\: in\: medium(v)}$
$n=\frac{c}{v}$
Note
According to Snell's law -
$\frac{sin \: i}{sin \: r}=\frac{n_{2}}{n_{1}} \quad\quad (1)$
$\frac{sin \: i}{sin \: r}=\frac{\frac{c}{v_{1}}}{\frac{c}{v_{2}}} \quad\quad \left \{ \because n=\frac{c}{v} \right \}$
$\frac{sin i}{sin r}=\frac{v_{1}}{v_{2}} \qquad (2)$
When the light goes from one medium to another medium frequency of the light does not change but the wavelength of the light changes. So above given equation can be written as
$\frac{sin \: i}{sin \: r}=\frac{\nu \lambda_{1}}{\nu \lambda_{2}} \quad\quad \left \{ \because v=\nu \lambda \right \} $
$\displaystyle \frac{sin \: i}{sin \: r}=\frac{\lambda_{1}}{ \lambda_{2}} \qquad (3)$
From equation $(1)$ ,equation $(2)$, and equation $(3)$ we can write the equation
$\frac{sin \: i}{sin \: r}=\frac{n_{2}}{n_{1}} =\frac{v_{1}}{v_{2}}= \frac{\lambda_{1}}{ \lambda_{2}}$
Conditions for a light ray to pass undeviated on refraction of light→
A ray of light passes undeviated from medium $1$ to medium $2$ in either of the following two conditions:
Factors affecting the refractive index of the medium→
The refractive index of a medium depends on basically following three factors:
1. Nature of the medium (on the basis of speed of light)→
Less the speed of light in the medium as compared to that in the air more is the refractive index of the medium.
$\left ( n=\frac{c}{v}\right)$
Speed of light in glass- $v_{glass} = 2\times 10^{6} ms^{-1}$
$\mu_{glass} = 1\cdot 5$
Speed of light in water- $v_{water} = 2\cdot25\times10^8ms^{-1}$
$\mu_{water} = 1\cdot33$
2. Physical conditions such as temperature→
With the increase in temperature, the speed of light in the medium, so the refractive index of the medium decreases.
3. The colour or wavelength of light→
The speed of light of all colours is the same in the air ( or vacuum), but in any other transparent medium, the speed of light is different for different colours. In a given medium the speed of red light is maximum and that of the violet light is least, therefore the refractive index of that medium is maximum for violet is and least for red light i.e. $\left ( \ n_{violet}> n_{red}\right )$. The wavelength of visible light increase from violet to red end, so the refractive index of a medium decreases with the increases in wavelength.
 |
| Propagation of light from rarer medium to denser medium |
 |
| Propagation of light from denser medium to rarer medium |
- The incident ray, normal ray, and refracted ray lie on the same point.
- According to Snell's law - The ratio of the sine of the incident angle to the sine of the refractive angle is always constant. This constant value is known as the refractive index of the medium.
- When the angle of incidence at the boundary of two media is zero $\angle i =0^{\circ} so \ \angle r= 0^{\circ}$.
- When the refractive index of the medium (2) and medium (1) is the same i.e. $i=r$.
Alternating Current Circuit containing Resistance only (R-Circuit)
Alternating Current Circuit containing Resistance (R-Circuit): Let us consider, An alternating current circuit containing resistance $R$ only. This resistance $R$ is connected with an alternating EMF i.e electromotive force source i.e.
$E=E_{\circ}sin\omega t\qquad(1)$
The potential difference across the circuit
$E=iR$
Then from equation $(1)$
$iR=E_{\circ}sin\omega t $
$i=\frac{E_{\circ}}{R}sin\omega t $
$i=i_{\circ}sin\omega t \qquad(2) $
Where $i_{\circ}$ is the peak value or amplitude of the current in the circuit which has value $i_{\circ}=\frac{E_{\circ}}{R}$.
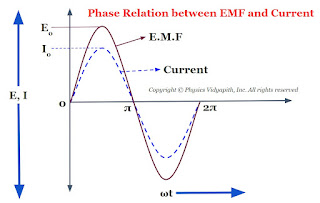
Now compare the equation $(1)$ and equation $(2)$ which shows that if a circuit is containing a resistor only then the current is always in phase with the applied EMF i.e electromotive force. The phase diagram between EMF and the current of resistance is shown below-
The phasor diagram between the EMF and current of resistance is also shown in the given figure below-
Derivation of Addition of Velocity in Special Relativity
Addition of Velocities:
Let us consider two frames $S$ and $S'$, frame $S'$ is moving with constant velocity $v$ relative to frame $S$ along the positive direction of the X-axis.
Let us express the velocity of the body in these frames. Suppose that body moves a distance $dx$ in time $dt$ in frame $S$ and through a distance $dx'$ in the time $dt'$ in the system $S'$ from point $P$ to $Q$. Then
$\frac{dx}{dt} = u\qquad \frac{dx'}{dt'}= u'\qquad (1)$
From Lorentz's inverse transformation
$x=\alpha\left ( x'+vt' \right )\qquad(2)$
$t=\alpha '\left ( t'+\frac{v\cdot x'}{c^{2}} \right )\qquad(3)$
Differentiate the equation $(2)$ and equation $(3)$ with respect to $t'$
$\frac{dx}{dt'}= \alpha \left ( \frac{dx'}{dt'}+v \right )\qquad(4)$
$\frac{dt}{dt'}= \alpha ' \left ({1}+\frac{v}{c^{2}} \cdot \frac{dx'}{dt'} \right )\quad (5)$
Now divide the equation $(4)$ by equation $(4)$. So
$\frac{\frac{dx}{dt'}}{\frac{dt}{dt'}} = \left ( \frac{\frac{dx'}{dt}+v}{1+\frac{v}{c^{2}}\cdot \frac{dx'}{dt'} } \right ) \qquad $
From Lorentz Transformation $\alpha =\alpha '$. So above equation can be written as:
$\frac{dx}{dt} = \frac{u' +v}{1+ \frac{u'v}{c^{2}}}$
From equation $(1)$. The above equation can be written as:
$u = \frac{u' +v}{1+ \frac{u'v}{c^{2}}} $
This equation represents the relativistic law of addition of velocities with respect to an observer at frame-$S$ whereas in classical mechanics it is simply $u = u'+v$. There is the following point observed from the addition of the velocities equation.
 |
| Addition of velocity |
- When $u'$ and $v$ are the smaller as compare to $c$, then $\frac{v\cdot u'}{c^{2}}$ can be negligible so
$u = u'+v$which is classical formula.
- When $u' = c$Then $u =\frac{c+v}{1+\frac{v}{c}}$ So,
$u=c$Therefore a object moves with velocity of light $c$ with respect to other, then their relative velocity is always $c$.
- When $v=u'=c$Then $u =\frac{c+c}{1+\frac{c^{2}}{c^{2}}}=c$ So,
$u=v$This shows that the addition of the velocity of light simply reproduces the velocity of light. It means that the velocity of light in a vacuum is the maximum achievable velocity in nature and no signal and any object can travel faster than the velocity of light in a vacuum.
Work done by a rotating electric dipole in uniform electric field
Derivation of Work done by a rotating electric dipole in uniform electric field :
Let us consider, An electric dipole AB, made up of two charges $+q$ and $-q$, is placed at a very small distance $2l$ in a uniform electric field $\overrightarrow{E}$. If dipole $AB$ rotates at angle $θ$ from its equilibrium position. If $A'$ and $B'$ are the new position of a dipole in the electric field. Then force on $+q$ charge particle due to electric field→
$ \overrightarrow{F_{+q}}=q\overrightarrow{E}\qquad (1)$
Then force on $-q$ charge particle due to electric field→
$ \overrightarrow{F_{-q}}=q\overrightarrow{E}\qquad(2)$
So work done by a force on $+q$ charge particle to bring from position $A$ to position $A'$→
$ \overrightarrow{W_{+q}}=\overrightarrow{F_{+q}}·\overrightarrow{AC}$
$ \overrightarrow{W_{+q}}=q\overrightarrow{E}· \overrightarrow{AC}\qquad(3)$
Similarly, work done by the force on $-q$ charge particle to bring from position $B$ to position $B'$→
$ \overrightarrow{W_{-q}}=\overrightarrow{F_{-q}}·\overrightarrow{BD}$
$ \overrightarrow{W_{-q}}=q\overrightarrow{E}· \overrightarrow{BD}\qquad (4)$
So the total work is done by the force on the dipole→
$ \overrightarrow{W}=\overrightarrow{W_{+q}}\:+\:\overrightarrow{W_{-q}}$
$\overrightarrow{W}=q\overrightarrow{E}·(\overrightarrow{AC}+\overrightarrow{BD})\qquad (5)$
From the figure, There is symmetry so
$ \overrightarrow{AC}=\overrightarrow{BD}$
So from equation $(5)$
$ \overrightarrow{W}=q\overrightarrow{E}·(2\overrightarrow{AC})$
$ \overrightarrow{W}=2q\overrightarrow{E}(\overrightarrow{AO}-\overrightarrow{CO})\qquad (6)$
From figure→
$ \left | \overrightarrow{AO} \right |=l$
$ \left | \overrightarrow{CO} \right |=l\:cos \theta$
Now substitute the values in equation (6). So equation (6) can be written as in magnitude form →
$ W=2qE(l-l\:cos\theta )$
$ W=2qEl(1-cos\theta )$
$ W=pE(1-cos\theta )$
The above expression shows that work is done on a rotating electric dipole in a uniform electric field.
Case (i):
If $\theta=0^{\circ}$, Then work done will be minimum
$W_{min}=0$
Case (ii):
If $\theta=90^{\circ}$, Then work done
$W=pE$
Case (iii):
If $\theta=180^{\circ}$, Then work done will be maximum
$W_{max}=2pE$
 |
| Work done by rotating an electric dipole |
Electric field Intensity due a uniformly charged Spherical Shell
Electric field intensity at a different point in the field due to the uniformly charged spherical shell:
Let us consider, a spherical shell of radius $R$ in which $+q$ charge is distributed uniformly on the surface of the sphere. Now find the electric field intensity at different points due to the spherical shell. These different points are:
1.) Electric field intensity at an external point of the spherical shell
2.) Electric field intensity on the surface of the spherical shell
3.) Electric field intensity at an internal point of the spherical shell
1. Electric field intensity at an external point of the spherical shell:
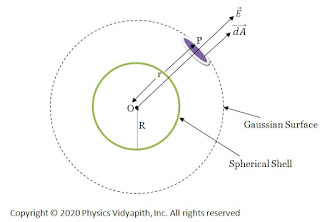
If point $O$ is the center of the spherical shell, The electric field at the outside of the spherical shell can be determined by the following steps →
1.) First, take the point $P$ outside the sphere
2.) Draw a spherical surface of radius r which passes through point $P$.This hypothetical surface is known as the Gaussian surface.
3) Now take a small area $\overrightarrow {dA} $ around point $P$ on the Gaussian surface to find the electric flux passing through it.
4.) Now find the direction between the electric field vector and small area vector.
Due to uniform charge distribution, the electric field intensity will be the same at every point on the Gaussian surface. So from the figure,
The direction of electric field intensity on the Gaussian surface is radially outward which is in the direction of the area vector of the Gaussian surface. i.e. ($\theta=0^{\circ}$).Here $\overrightarrow {dA}$ is small area around point $P$ so the small electric flux $d\phi_{E}$ will pass through this small area $\overrightarrow {dA}$. so this flux can be found by applying the Gauss's law in question given below:
$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$
$ d\phi_{E}= E\:dA\: cos 0^{\circ} \qquad \left \{\because \theta=0^{\circ} \right \}$
$ d\phi_{E}= E\:dA \qquad (1) \quad \left\{\because cos0=1 \right \}$
The electric flux passing through the entire Gaussian surface, So integrate the equation $(1)$ →
$ \phi_{E}=\oint E\:dA\qquad(2)$
According to Gauss's law:
$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$
From equation (1) and equation (2), we can write as
$ \frac{q}{\epsilon_{0}}=\oint E\:dA$
$ \frac{q}{\epsilon_{0}}= E\oint dA$
The area of entire Gaussian spherical is $\oint {dA}=4\pi r^{2}$. Now substitute this value in above equation. So above equation can be written as:
$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$
$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}$
From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged spherical shell is the same as, like the entire charge is placed at the center, point charge
If the surface charge density is $\sigma$, Then total charge $q$ on the surface of a spherical shell is →
$ q=4\pi R^{2}\: \sigma$
Substitute this value of charge $q$ in above equation, so we can write the equation as:
$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi R^{2}\: \sigma}{r^{2}}$
$ E=\frac{\sigma}{\epsilon_{0}}\frac{R^{2}}{r^{2}}$
This equation describes the electric field intensity at the external point of the spherical shell.
2. Electric field intensity on the surface of the spherical shell:
If point $P$ is placed on the surface of the spherical shell i.e ($r=R$). so electric field intensity on the surface of the spherical shell can be found by putting $r=R$ in the formula of the electric field intensity at the external point of the spherical shell:
$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{R^{2}}$
$ E=\frac{\sigma}{\epsilon_{0}}$
3. Electric field intensity at an internal point of the spherical shell:
If point $P$ is placed inside the spherical shell then the electric field intensity will be zero at that point because the charge is distributed uniformly on the surface of the solid sphere so there will not be any charge on the Gaussian surface and electric flux will be zero inside the solid sphere. i.e.
$ \phi_{E}=\oint E\:dA$
$ 0=E\oint dA \qquad \left \{ \because \phi_{E}=0 \right \}$
$ E=0$
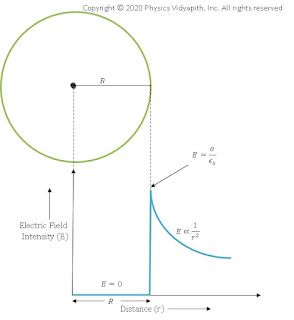
Electric field intensity distribution with distance for Spherical Shell:
Electric field intensity distribution with distance shows that the electric field is maximum on the surface of the sphere and zero inside the sphere. Electric field intensity distribution outside the sphere reduces with the distance according to $E=\frac{1}{r^{2}}$.
2.) Electric field intensity on the surface of the spherical shell
3.) Electric field intensity at an internal point of the spherical shell
2.) Draw a spherical surface of radius r which passes through point $P$.This hypothetical surface is known as the Gaussian surface.
3) Now take a small area $\overrightarrow {dA} $ around point $P$ on the Gaussian surface to find the electric flux passing through it.
4.) Now find the direction between the electric field vector and small area vector.
 |
| Electric field intensity due to the uniformly charged |
 |
| Electric field intensity distribution with distance |
Energy distribution laws of black body radiation
1.) Wein’s laws of Energy distributions→
A.) Wein's Fifth Power law→
The total amount of the energy emitted by a black body per unit volume at an absolute temperature in
the wavelength range $\lambda$ and $\lambda + d\lambda$ is given as
$E\lambda \cdot d\lambda= \frac{A}{\lambda^{5}}f\left ( \lambda T \right ) \cdot d\lambda \qquad (1)$
Where $A$ is a constant and $f(\lambda T)$ is a function of the product $\lambda T$ and is given as
$ f\left ( \lambda T\right )=e^-\frac{hc}{\lambda kT}\qquad (2)$
From equation $(1)$ and $(2)$
$E_\lambda \cdot d\lambda = \frac{A}{\lambda ^{5}}e^\frac{-hc}{\lambda kT} \cdot d\lambda$
$E_\lambda \cdot d \lambda = A \lambda ^{-5} e^\frac{-hc}{\lambda kT} \cdot d \lambda$
Wien’s law energy distribution explains the energy distribution at the short wavelength at higher
temperatures and fails for long wavelengths.
B.) Wein's Displacement law→
As the temperature of the body is raised the maximum energy shift toward the shorter wavelength i.e.
$\lambda_{m} \times T = Constant $
Where
$\lambda_m$- Wavelength at which the energy is maximum
$T$-Absolute temperature
Thus, if radiation of a particular wavelength at a certain temperature is adiabatically altered to another wavelength then temperature changes in the inverse ratio.
2.) Rayleigh-Jean’s law→
The total amount of energy emitted by a black body per unit volume at an absolute temperature T in the wavelength range $\lambda $ and $\lambda +d\lambda $ is given as
$E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{4}}.d\lambda$
Where K– Boltzmann’s Constant which has valve $ 1.381\times 10^{23}\frac{J}{K}$
This law, explains the energy distribution at the longer wavelength at all temperatures and fails totally for the shorter wavelength.
Note→
The energy distribution curves of the black body show a peak while going towards the ultraviolet wavelength (shorter $ \lambda $) and then fall while Rayleigh-Jeans law indicates continuous rise only. This is the failure of classical physics.
3.) Stefan-Boltzmann Law→
The total amount of heat radiated by a perfectly black body per unit area per second is directly proportional to
the fourth power of its absolute temperature $(T)$. i.e.
$E \propto T^{4}$
$E = \sigma T^{4}$
Where $\sigma$= Stefan’s Constant which has value $5.67\times 10^{-8} W-\frac{K^{4}}{m^{2}}$
It is a black body at absolute temperature $T$ is surrounded by another black body at absolute temperature $T_{0}$, The net amount of heat $E$ lost by the former per second per $cm^{2}$ is→
$E=\sigma (T^{4}-T_{0}^{^{4}})$
$\lambda_m$- Wavelength at which the energy is maximum
$T$-Absolute temperature
Relation between group velocity and phase velocity
We know that phase velocity
$V_{p}=\frac{\omega }{k}$
$\omega =V_{p}.k \qquad(1)$
And group velocity
$V_{g}=\frac{d\omega}{dk} \qquad(2)$
Substitute the value of $\omega$ from equation$(1)$ in equation $(2)$
$V_{g}=\frac{d}{dk}(V_{p}.k)$
$V_{g}=V_{p}+k.\frac{dV_{p}}{dk}$
$V_{p}=V_{p}+k.\frac{dV_{p}}{d\lambda}.\frac{d\lambda }{dk} \qquad (3)$
But
$\lambda=\frac{2\pi }{k}$
The above equation can be obtain from following formula i.e. $k=\frac{2\pi}{\lambda }$
Now put the value of $\lambda$ in equation $(3)$
$V_{g}=V_{p}+k\frac{dV_{p}}{d\lambda}\frac{d}{dk}(\frac{2\pi }{k}$
$V_{g}=V_{p}+k\frac{dV_{p}}{d\lambda}(\frac{-2\pi }{k^{2}}$
$V_{g}=V_{p}-\frac{2\pi}{k}\frac{dV_{p}}{d\lambda }$
$V_{g}=V_{p}-\lambda\frac{dV_{p}}{d\lambda }$
Thus, the above equation represents the relation between group velocity and phase velocity.
Electric Line of Force and its Properties
Electric Field:
The size and magnitude of the test charged particle is very small i.e tends to zero which does not modify the electric field of source charged particle. The electric field can only experience, not be seen by eyes. The electric field is defined by imaginary lines which are called electric field lines.
Electric Field Lines:
Electric field lines are imaginary lines that describe the behavior of electric fields. The behavior of the electric field tells about the force acting on free test-charged particles. This force gives the motion to the free test charge particle which is placed in the path of the electric field line. So the test charged particle moves in the direction of the electric field line. Hence, the direction of electric force and electric field lines both are the same. Thus electric field line is also known as electric lines of force.
Electric Lines of Force:
Properties of Electric Line of Force:
There are the following properties of the electric line of force:
1.) The direction of the electric line of force is outward for positively charged particles, and inward for negatively charged particles.
So when two opposite charge are placed near each other, the electric line of force start from a positive charge and end at a negative charge
When two same nature charges are placed near each other, the field produced by one charge is equal and opposite to the field produced by the other charges at the midpoint of the line joining the two charges. Therefore, at this point, the resultant electric field is zero. This point is called the neutral point.
2.) The tangent drawn at any point on the line of force gives the direction of the force acting on a test-charged particle at that point.
3.) Two electric lines of force can never intersect with each other because if they do so then at the point of intersection two tangents can be drawn which would mean that there are two directions of the force at that point which is impossible.
4.) When electric lines of force are closer to each other, the electric field is stronger in this region. And where The line of force are far away from each other then the electric field is weaker in this region. When the line of force are parallel and in a straight line to each other, the electric field is known as the uniform electric field.
5.) The electric line of force has a tendency to contract in length like a stretched elastic string for the opposite nature of the charged particle. It is due to the attraction force between charged particles.
6.) The electric line of force has a tendency to separate from each other in the direction perpendicular to their length for the same nature of charged particles. It is due to the repulsion force between charged particles.
7.) The electric lines of force can never form closed loops as a line can never start and end on the same charge.
8.) The electric line of force also gives us an indication of the equipotential surface (That surface which has the same potential on each point of the surface).
9.) The electric line of force always flows from higher potential to lower potential.
10.) In a region where there is no electric field, lines are absent so the electric field inside the conductor is zero. Electric lines of force end or start normally from the surface of a conductor.
That region around any charged particle (source-charge) in which other test charged particle experience an electric force (attraction or repulsion). This region is called electric field of that charged particle.
An electric line of force is defined as an imaginary smooth curve drawn in electric field along which a free isolated test charged particle moves. The tangent drawn at any point on the electric line of force gives the direction of the force acting on a test charged particle placed at that point.
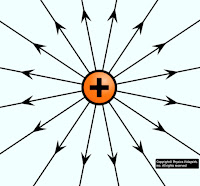 |
| Electric field line of positive charge |
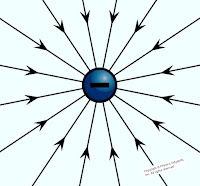 |
| Electric field line of negative charge |
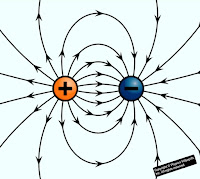 |
| Electric lines of force of unlike charges |
 |
| Electric lines of force of like charges |
Electric Charge and its properties
What is an electric charge?
Types of charge:
There are two types of electric charge
1.) Positive Electric Charge like Proton
2.) Negative Electric Charge like Electron
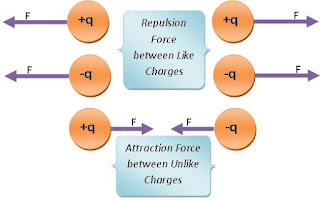
The same nature of charged particles repels each other and the opposite nature of charged particles attracts each other. For example, electrons and electrons repel each other, and electrons and protons attract each other. Similarly, proton and proton repel each other.
Generally, any substance is electrically neutral because the number of electrons and protons are equal in it but according to the Free electron Model theory, these substances are classified into three categories. These are:
1.) Conductor
2.) Semiconductor
3.) Insulator
The electric force is generated in conductors and insulating substances but not in semiconductor substances because these semiconductor substances have four electrons in their valence shells.
Generation of Electric force in Conductor:
The electric force is generated in conductors due to the transfer of electrons from one conducting substance to another conducting substance.
There are various methods for the transfer of electrons in conductors, like contact, friction, and induction. Therefore, When electrons are transferred from one conductor to another conductor then the conductor has deficiency or excess of electrons, these conductors are called electrostatically charged.
Electrostatic charged Conductors:
There are two types of electrostatic-charged conductors.
1.) Positive Electrostatic Charged Conductor:
When conductors have a deficiency of electrons i.e. the number of electrons is less than protons, these conductors are called positive electrostatic charged conductors.
2.) Negative Electrostatic Charged Conductor:
When conductors have excessive electrons i.e. number of electrons is greater than protons, these conductors are called negative electrostatic charged conductors.
Generation of Electric force in Insulator:
Insulators are charged by induction this charging occurs due to the polarization of atoms of insulating substances. In the absence of an external electric field, the center of mass of the nucleus and electron cloud in an atom lies on the same point but when an insulating substance is placed in an external electric field, the center of mass of the nucleus and electron cloud in an atom is separated from each other at a very small distance. The center of mass of the electron cloud is shifted toward the positive side of the external electric field and the center of mass of the nucleus is shifted toward the negative side of the external electric field. thus these atoms are polarized. When insulators are electrically charged, these polarized atoms store the electric potential energy.
Basic Properties of Electric Charge:
1.) Additive Nature of Charge:
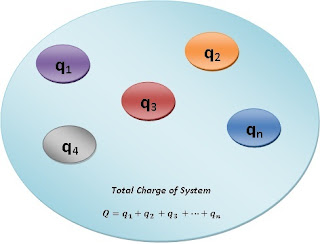
If a system contains $'n'$ number of point charges, the total charge of a system will be the sum of $'n'$ number of point charges.
Let us consider, a system containing $'n'$ number of point charges like $q_{1},q_{2},q_{3}......q_{n}$, the total charge of the system will be
$Q=q_{1}+q_{2}+q_{3},.....+q_{n}$
$Q=\sum_{i}^{n}q_{i}$
2.) Conservation of Charge:
The total Charge of the isolated system is always conserved i.e.
3.) Quantization of Charge:
The electric charge is always an integer multiple of $‘e’$. It is known as the quantization of charge.
$Q=\pm ne$
Where $'n'$ is an integer number.
4.) The mass of charged particle depends on velocity:
The velocity of the charged particle is significant to the speed of light so the mass of the charged particle depends on the velocity. This variation can be found by following the formula:
$m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$
Where
$m_{0}$ - Rest mass of particle
$m$ - Relative mass of the particle
Electric charge is an intrinsic property of elementary particles (e.g., electrons, protons, neutrons, etc.) of any substance that gives rise to electric force between them when they get closer.
2.) Negative Electric Charge like Electron
2.) Semiconductor
3.) Insulator
The charge on the conductors due to the transfer of electrons between the conductors is known as electrostatic charged conductor.
The total charge on any system is always equal to the algebraic sum of all the charges in the system.
The electric charges neither can be created nor destroyed i.e. The electric charges are generated due to transfer of electrons from one subtance to another substance.
$m_{0}$ - Rest mass of particle
$m$ - Relative mass of the particle
Electric Potential and Derivation of electric potential at a point due to point charged particle
Electric Potential:
When a test-charged particle is brought from infinity to a point in the electric field then the work done per unit test charge particle is called electric potential. It is represented by $V$. It is a scalar quantity.
Let's consider a test-charged particle $q_{0}$ bring from infinity to at a point $P$ in the electric field. If the work done by test charged particle is $W$ then electric potential →
$V=\frac{W}{q_{0}}$
Unit of Electric Potential: $Joul/Coulomb$ OR $N-m/Ampere-sec$
In MKS: $Kg-m^{2}-Ampere^{-1}-sec^{-3}$
Dimension of Electric potential: $[ML^{2}A^{-1}T^{-3}]$
The electric potential at a point due to point charged particle:
Let us consider, a source point charge $+q$ is placed in air and vacuum at point $O$.Let's take a point $P$ at distance $r$ from the source point charged particle. Here the test-charged particle $+q_{0}$ is brought from infinity to point $P$.If the test-charged particle moves a very small distance $dx$ from point $A$ to $B$ against the electrostatic force. So electrostatic force at point $A$ which is placed at a distance $x$ from point $O$ →
$F=\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}} \qquad(1)$
The work is done against the electrostatic force $\overrightarrow{F}$ to move small distance $dx$ from point $A$ to Point $B$
$ dW=\overrightarrow{F}\: \overrightarrow{dx}$
$ dW=F\: dx \: cos 180^{\circ}$
Here the angle between the electrostatic force and displacement is $180^{\circ}$. So work done
$ dW=- F\: dx$
$ dW=-\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}}\:dx \qquad \left\{ from\: equation \: (1) \right\}$
The total work is done in moving the charge $q_{0}$ from infinity to the point $P$ will be
$W=-\int_{0}^{W}{dW}$
Here negative sign shows that the work done from infinity to at point $P$ is stored in the form of potential energy between the charges.
$ W=-\int_{\infty}^{r}{\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}}\:dx }$
$ W=-\frac{qq_{0}}{4\pi\epsilon{0}} \int_{\infty}^{r}{\frac{dx}{x^{2}} }$
$W=-\frac{qq_{0}}{4\pi\epsilon{0}} \left [\frac{-1}{x} \right ]_{\infty}^{r}$
$ W=-\frac{qq_{0}}{4\pi\epsilon{0}} \left [-\frac{1}{r}-\frac{-1}{\infty} \right ]$
$W=\frac{qq_{0}}{4\pi\epsilon{0}} \left [\frac{1}{r} \right ]$
$ W=\frac{1}{4\pi\epsilon{0}} \left [\frac{qq_{0}}{r} \right ]$
Hence, the work is done to move a unit test charge from infinity to the point $P$, or the electric potential at point $P$ is →
$V=\frac{W}{q_{0}}$
$V=\frac{1}{4\pi\epsilon{0}} \frac{q}{r}$
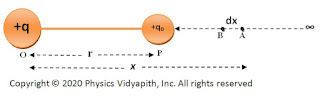 |
| Electric potential due to point charge |
Construction and Working of Nuclear Reactor or Atomic Pile
A nuclear reactor is a device within which a self-sustaining controlled chain reaction is produced by fissionable material. it is thus a source of control energy that is utilized for several useful purposes. The reactor has some important part which is given below:
Construction:
It is made up of a large number of uranium rods which are placed in calculated geometrical lattice between layers of pure graphite ( moderator) blocks. To
prevent oxidation of Uranium, the rods are covered by close-fitting
aluminum cylinders. The control rods are so inserted within the lattice that they will be raised or lowered between the Uranium rods whenever necessary. The whole reactor is encircled by a concrete shield.
Working:
The actual operation of the reactor is started by pulling out the control rods so that they do not absorb many neutrons. Then, the stray neutrons,
which are always present in the tractor, start fissioning the U-235 nuclei.
In each fission, two or three fast neutrons are produced. These neutrons repeatedly strike the moderator and slowed down. Then, These neutrons start fissioning the U-235 nuclei. So, a chain-reaction of fission starts. The number of neutrons, which is produced in fissioning, is controlled by pushing the cadmium rods into the reactor. These rods absorb a number of the neutrons. Thus, the energy produced in the reactor is kept under control to avoid any explosion. The coolant is pond pumped through the reactor to carry away The Heat generated by the fission of uranium nuclei. the hot CO2 passes through the heat exchanger and convert cold water into steam. This steam is used to operate turbines for generating electricity.
- Fuel: The fassionable material such as Uranium-235 and Plutonium-239 known as fuel. These materials play an important role in operating the nuclear reactor.
- Moderator: It slows down the neutrons to thermal energies through the elastic collision between its nuclei and fission neutrons. Thermal neutrons have a very high probability of fissioning Uranium-235 nuclei. Examples: heavy water graphite beryllium oxide. Heavy water is the best moderator.
- Control Rods: These rods are used to control the fission rate in the reactor. these Rods are fixed in the reactor walls. These rods are made up of the material of cadmium and Boron. These materials are good absorbers of slow neutrons. Therefore when the rods are pushed into the reactor, the fission rate decreases, and when they are pulled out, the fission grows.
- Coolant: The coolant is used to remove the heat from the reactor which is produced inside the reactor. For this purpose air-water or CO2 is passed through the reactor.
- Shield: various type of intense rays are emitted from the reactor, which may be injurious to the people working near the reactor. To protect them from this radiation, thick concrete walls are erected around the reactor.
- Safety device: In case of an accident or other emergency, a special set of control rods, called " shut-off rods" enter the reactor automatically. They immediately absorb the neutrons so that the chain reaction stops entirely.
Popular Posts
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(10)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(2)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(4)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(1)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(33)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)