Description of Displacement Current:
The concept of displacement current was first introduced by Maxwell purely on the theoretical ground.
Maxwell postulates that "It is not only current in a conductor that produces a magnetic field but a changing electric field (or time varying electric field) in vacuum or in dielectric also produces the magnetic field. It means that a changing electric field is equivalent to a current which flows as long as the electric field is changing. This equivalent current in a vacuum or dielectric produces the same magnetic effect as an ordinary or conductor current in a conductor. This equivalent current is known as displacement current".
According to the Maxwell modified ampere's law.
$\oint \overrightarrow{B}. \overrightarrow{dl}= \mu_{\circ}i+\mu_{\circ}i_{d}$
Where $i_{d}$ = Displacement Current
Mechanism of Flow of Charge in Metals: Free Electron Gas Theory
Theory of Free Electron Gas Model →
According to the electron gas theory
1. The free electrons are continuous in motion inside the metal. The motion of free electrons are random inside the metal.
2. When the free electrons are collisied to each other then the direction of electrons are changed.
3. Mean free Path: The length covered by free electrons, between the two successive collisions is called the "Mean Free Path".
4. Relaxation Time: The time taken between the two successive collisions of free electrons is called the Relaxation time. It is represented by $\tau$.
5. Drift velocity: When a potential is applied across the metal then these electrons do not move own velocity but it move with an average velocity in the opposite direction of the electric field. This average velocity is called the "Drift Velocity". The drift velocity of electrons depends upon the applied potential.
6. Mobility of Electrons: When a potential $V$ is applied across the metal then electrostatic force $F$ acts on the electrons i.e
$F=qE $
$F=NeE \qquad(1)$
Where
$N$ →The number of free electrons inside the metal
$E$ → The electric field due to the applied potential
When this electrostatic force is applied to the electrons then these electrons are accelerated with accelerated $a$ i.e
$F=ma \qquad(2)$
From equation $(1)$ and equation $(2)$ we can write
$ma=N\:e\:E$
$a=\frac{N}{m}eE$
$\frac{v_{d}}{\tau}=\frac{N}{m}eE \qquad \left( \because a=\frac{v_{d}}{\tau} \right)$
$v_{d}=\frac{Ne\tau}{m} E$
$v_{d}=\mu E$
Where $\mu=\frac{Ne\tau}{m}$. It is known as the mobility of electrons.
$N$ →The number of free electrons inside the metal
$E$ → The electric field due to the applied potential
Derivation of Ohm's Law
Derivation→
Let us consider,
The length of the conductor = $l$
The cross-section area of the conductor = $A$
The potential difference across the conductor = $V$
The drift velocity of an electron in conductor = $v_{d}$
Now from the equation of the mobility of electron i.e.
$v_{d}= \mu E$
$v_{d}= \left( \frac{e\tau}{m} \right) E \qquad \left(\because \tau = \frac{e\tau}{m} \right)$
$v_{d}= \left( \frac{e\tau}{m} \right) \frac{V}{l}\qquad (1) \qquad \left(\because E = \frac{V}{l} \right)$
Now from the equation of drift velocity and electric current
$i=neAv_{d}$
Now substitute the value of $v_{d}$ from equation $(1)$ to above equation
$i=neA\left( \frac{e\tau}{m} \right) \frac{V}{l}$
$i=\left( \frac{ne^{2}A\tau}{ml} \right)V$
$\frac{V}{i}=\left( \frac{ml}{ne^{2}A\tau} \right)$
$\frac{V}{i}=R$
Where $R = \frac{ml}{ne^{2}A\tau} $ is known as electrical resistance of the conductor.
Thus
$V=iR$
This is Ohm's Law.
The cross-section area of the conductor = $A$
The potential difference across the conductor = $V$
The drift velocity of an electron in conductor = $v_{d}$
Relation between electric current and drift velocity
Derivation→
Let us consider
The length of the conductor = $l$
The cross-section area of the conductor = $A$
The total number of free electrons inside the conductor = $N$
The current flow in the conductor = $i$
The Relaxation time between the two successive collisions =$\tau$
According to the law of current density
$J=\frac{i} {A} $
$J=\frac{q} {A \tau} \qquad \left( \because i=\frac{q}{\tau} \right)$
$J=\frac{N \: e }{A \tau} \qquad \left( \because q=Ne \right)$
Now multiply by length of conductor $l$ in above equation. Therefore we get
$J=\frac{N \: e \: l}{A \tau\: l} $
$J=\frac{N \: e \: l}{V \tau\: }\qquad \left(\because V=A.l \right)$
Where $V$ is volume of the conductor.
$J=\frac{n \: e \: l}{ \tau }\qquad \left( \because n=\frac{N}{V} \right)$
Where $n$ is total number of electrons per unit .
$J=n \: e \: v_{d}\qquad \left( \because v_{d}=\frac{l}{\tau}\right)$
Where $v_{d}$ are known as drift velocity of charged particles.
Now substitute the value of current density $J$ from equation $(1)$ to above equation then above equation can be written as
$i=neAv_{d}$
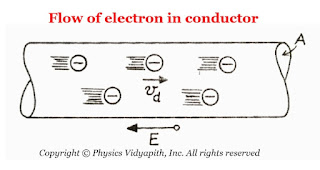 |
| The flow of Electron in Conductor |
Energy Stored in a Charged Capacitor
Description→
When a capacitor is charged, the work is done by charged battery (i.e the chemical energy of the battery is used to charge the capacitor). As the capacitor gets charged, the potential difference between its plates increases. Due to this increase in the potential difference between the plates, the battery has to give the same amount of charge to the capacitor. Because of that, the battery has to do more and more work.
The total amount of work done in charging the capacitor is stored in the form of electric potential energy in between the capacitor plates. This energy is retrieved as heat when the capacitor is discharged through a resistance.
Derivation→
Let us consider, a capacitor of capacitance $C$with a potential difference of $V$ between the plates.
In the process of charging, electrons are transferred from the positive to negative, unit each plate acquires an amount of charge $q$. Suppose during the process of charging, we increase the charge from $q'$ to $q'+dq'$ by transferring an amount of negative charge $dq'$ from the positive to the negative plate. the work done
$dw=V' \: dq'$
$dw=\frac{q'}{C} \: dq'$
Therefore, the total work done in charging the capacitor from the uncharged state (i.e. zero charge in the capacitor) to the final charge $q$ will be
$W=\int_{0}^{W} dw$
$W=\int_{0}^{q} \frac{q'}{C} \: dq'$
$W=\frac{1}{2}\left[ \frac{q'^{2}}{C} \right]^{q}_{0} $
$W=\frac{1}{2}\left[ \frac{q^{2}}{C} \right]$
$W=\frac{1}{2}\:C \: V^{2}$
This work done is stored in the form of potential energy $U$ within the capacitor. Thus
$U=\frac{1}{2}\:C \: V^{2} $
$U=\frac{1}{2}\frac{q^{2}}{C}$
Energy Stored in Combination of Capacitor→
If many capacitors are combined in series, or in parallel, the total potential energy stored in either combination is equal to the sum of the potential energies stored in the individual capacitor. This follows from the combination of the capacitor's expressions:
The potential energy is stored in a series combination→
The potential energy stored in a series combination (here $q$ is constant) is
$U=\frac{1}{2}\frac{q^{2}}{C}$
For series combination the capacitance of capacitor i.e. $\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{2}}+..........$. Now substitute the value of $\frac{1}{C}$ in above equation
$U=\frac{1}{2}q^{2} \frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{2}}+.......... $
$U= \left( \frac{1}{2}q^{2} \frac{1}{C_{1}}+\frac{1}{2}q^{2} \frac{1}{C_{2}}+ \frac{1}{2}q^{2} \frac{1}{C_{2}}+.......... \right)$
$U=U_{1}+U_{2}+U_{3}+.........$
The potential energy is stored in a parallel combination→
The potential energy is stored in a parallel combination (here $V$ is constant) is
$U=\frac{1}{2}CV^{2}$
For parallel combination the capacitance of capacitor i.e. $C=C_{1}+C_{2}+C_{3}+......$. Now substitute the value of $C$ in the above equation
$U=\frac{1}{2} \left( C_{1}+C_{2}+C_{3}+........... \right) V^{2}$
$U= \frac{1}{2} C_{1} V^{2} + \frac{1}{2} C_{2} V^{2} +\frac{1}{2} C_{3}V^{2} +..... $
$U=U_{1}+U_{2}+U_{3}+......$
Force between the plates of a Charged Parallel Plate Capacitor
Derivation and Description→
Consider, A parallel plate capacitor with a charge $+q$ on one of its plates and $-q$ on the other plate. Let initially the plates of the capacitor are almost, but not quite touching. Due to opposite polarity, there is an attractive force $F$ between the plates. Now If these plates are gradually pulling and apart to a distance $d$, in such a way that $d$ is still small compared to the linear dimension of the plates, then the approximation of a uniform field between the plates is maintained and thus the force remains constant.
Now the work done in separating the plates from near $0$ to $d$,
$W=F.d \qquad(1)$
This work done $(W)$ is stored as electrostatic potential energy $(U)$ between the plates, i.e.
$U=\frac{1}{2}q V $
But $V=E.d$, then the above equation can be written as
$U=\frac{1}{2}q \: E \: d \qquad(2)$
But the equation $(1)$ and equation $(2)$ both are equal then
$F.d=\frac{1}{2}q \: E \: d$
$ F=\frac{1}{2}q \: E $
The factor $\frac{1}{2}$ arises because just outside the conducting plates the field is $E$ and inside the plates, the field is zero. So the average value $\frac{E}{2}$ contributes to the force.
 |
| The force between the charged parallel plates of the capacitor |
Capacitance of a Parallel Plate Capacitor Partly Filled with Dielectric Slab between Plates
Derivation→
Let us consider,
The charge on a parallel-plate capacitor = $q$
The area of parallel-plate = $A$
The distance between the parallel-plate = $d$
The dielectric constant of the slab of a material =$K$
The thickness of the material =$t$
The vacuum (or air) between the plates =$(d-t)$ The surface charge density on the plates= $\sigma$
The electric field in the air between the plates is
$E_{\circ}=\frac{\sigma}{\epsilon_{\circ}}$
$E_{\circ}=\frac{q}{\epsilon_{\circ}\: A} \qquad(1)$
The electric field in the dielectric material
$E=\frac{q}{\epsilon_{\circ}\: K\: A} \qquad(2)$
The potential difference between the plates
$V=E_{\circ}\left( d-t \right)+E\:t \qquad(3)$
Now substitute the value of $E_{\circ}$ and $E$ in the equation $(3)$, Then we get
$V=\frac{q}{\epsilon_{\circ}\: A} \left( d-t \right)+ \frac{q}{\epsilon_{\circ}\: K\: A} \:t $
$V=\frac{q}{\epsilon_{\circ}\: A} \left[ \left( d-t \right)+ \frac{t}{K} \right] \qquad$
The capacitance of the capacitor is
$C=\frac{q}{V}$
Now substitute the value of electric potential $V$ in the above equation then
$C= \frac{q}{\frac{q}{\epsilon_{\circ}\: A} \left[ \left( d-t \right)+ \frac{t}{K} \right]}$
$C= \frac{\epsilon_{\circ}\: A}{\left[ \left( d-t \right)+ \frac{t}{K} \right]} $
Since $K>1$, the 'effective' distance between the plates becomes less than $d$ and so the capacitance increases.
Special Cases→
The area of parallel-plate = $A$
The distance between the parallel-plate = $d$
The dielectric constant of the slab of a material =$K$
The thickness of the material =$t$
The vacuum (or air) between the plates =$(d-t)$ The surface charge density on the plates= $\sigma$
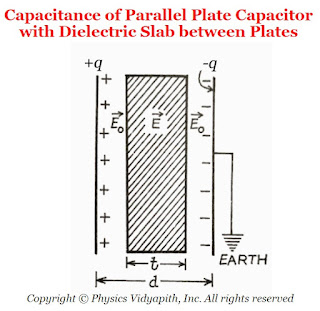 |
| The capacitance of Parallel Plate Capacitor with Dielectric Slab between Plates |
- When the dielectric slab is completely filled between the parallel plates i.e. $t=d$ then the capacitance between the parallel plates
$C= \frac{K \: \epsilon_{\circ}\: A}{d}$
- When there is a vacuum (or air) between the parallel plates i.e. $t=0$, then the capacitance between the parallel plates
$C_{\circ}= \frac{ \epsilon_{\circ}\: A}{d}$
- When there is a slab of metal whose dielectric constant is infinity (K=∞). If the thickness of the slab is t between the parallel plates, then the capacitance between the parallel plates
$C= \frac{ \: \epsilon_{\circ}\: A}{d-t}$
- When the slabs of dielectric constants $K_{1},K_{2},K_{3},K_{4}...........$ and respective thickness $t_{1},t_{2},t_{3},t_{4},........$ is placed in the entire space between the parallel-plates, then the capacitance between the plates
$C=\frac{\epsilon_{\circ} A}{d- \left( t_{1}+t_{2}+t_{3}+.... \right)+ \left( \frac{t_{1}}{K_{1}}+\frac{t_{2}}{K_{2}}+\frac{t_{3}}{K_{3}}+....... \right)}$But $d=t_{1}+t_{2}+t_{3}+....$$C=\frac{\epsilon_{\circ} A}{ \left( \frac{t_{1}}{K_{1}}+\frac{t_{2}}{K_{2}}+\frac{t_{3}}{K_{3}}+..... \right)}$
Parallel Plate Air Capacitor and Its Capacitance
Parallel Plate Air Capacitor→
A parallel-plate capacitor consists of two long, plane, metallic plates mounted on two insulating stands and placed at a small distance apart in a vacuum (or air). The plates are exactly parallel to each other.
Derivation of the capacitance of parallel plate capacitor in the air→
Let us consider, Two plates $X$ and $Y$ are separated at a small distance $d$ in the vacuum (or air). If the area of plates is $A$ and the plates $X$ and $Y$ have charge $+q$ and $-q$ respectively. If the surface charge density on each plate is $\sigma$ then electric field intensity at a point between two parallel plates is
$E=\frac{\sigma}{\epsilon_{\circ}}$
$E=\frac{q}{\epsilon_{\circ}A}\qquad(1) \qquad (\because \sigma=\frac{q}{A}) $
The potential difference between the parallel plates capacitor in air (or vacuum) is
$V=E.d$
Now substitute the value of $E$ from equation$(1)$ in the above equation
$V=\frac{q}{\epsilon_{\circ}A}.d \qquad(2)$
The capacitance of the parallel plate capacitor in air (or vacuum) is
$C_{\circ}=\frac{q}{V} \qquad(3)$
From equation $(2)$ and equation $(3)$
$C_{\circ}=\frac{q}{\frac{q}{\epsilon_{\circ}A}.d}$
$C_{\circ}=\frac{\epsilon_{\circ}A}{d}$
If the space between the plates is filled with some dielectric medium of dielectric constant $K$, then the electric field between the plates is
$E=\frac{\sigma}{K \: \epsilon_{\circ}}$
The Potential difference between the parallel plates when dielectric medium $(K)$ is present between them
$V=\frac{q}{K \: \epsilon_{\circ} \: A}.d $
Now, The capacitance of the parallel-plate capacitor when the dielectric medium $(K)$ is present between them
$C=\frac{K\: \epsilon_{\circ} \: A}{d}$
 |
| Parallel Plate Air Capacitor |
Potential Energy of a Charged Conductor
Definition:
Derivation →
Let us consider, a conductor of capacitance $C$. If charge $+Q$ is given into small amount of $dq$ to the surface of the conductor. Then the work done will be
$dw=V\:dq \qquad(1) $
$dw=\frac{q}{C} \:dq \qquad \left (\because V=\frac{q}{C} \right)$
Therefore, as the amount of charge on the conductor will increase from $0$ to $Q$ that causes also increase in work done. So integrate the above equation for total work done
$ \int_{0}^{W} dw=\frac{1}{C} \int_{0}^{Q} q dq$
$W=\frac{1}{C} \int_{0}^{Q} q dq$
$W=\frac{1}{C} \left[ \frac{q^{2}}{2} \right]^{Q}_{0}$
$W=\frac{1}{2} \frac{Q^{2}}{C}$
This work is stored in the form of electric potential energy $U$. Then
$U=\frac{1}{2} \frac{Q^{2}}{C}$
$U=\frac{1}{2} C V^{2}$
$U=\frac{1}{2} Q V$
The work done in charging the conductor is stored as potential energy in the electric field in the vicinity of the conductor is called the potential energy of a charged conductor.
Capacitance of an Isolated Spherical Conductor
Derivation →
Let us consider an isolated spherical conductor of radius $a$ is placed in a vacuum or air. Let a charge $+q$ be given to the sphere and this charge is distributed uniformly on the surface of conducting sphere. Then the electric potential at the surface of the conducting sphere is
$V=\frac{1}{4\pi \epsilon_{\circ}} \frac{q}{a} \qquad(1)$
So the capacitance of the sphere
$C=\frac{q}{V} \qquad(2)$
Now substitute the value of $V$ in equation $(2)$ Then we get
$C=\frac{q}{\frac{q}{4\pi \epsilon_{\circ}a}}$
$C=4\pi \epsilon_{\circ}a$
Thus, The capacitance of a spherical conductor is directly proportional to its radius. i.e If the radius of conducting sphere is large then the sphere will hold a large amount of the given charge without running up too high a voltage.
Unit:
The unit of capacitance is "Farad" i.e. $F$
 |
| Capacitance of an Isolated Spherical Conductor |
Popular Posts
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(10)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(1)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(4)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(1)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(33)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)




