Newton's Corpuscular Model

Newton's Corpuscular Theory

In the year 1675, Newton proposed the corpuscular theory of light to explain the existing phenomenon of light. There are the following assumptions of this theory:

1. The light consists of very small, lightweight, and invisible particles. These particles are known as corpuscles.

2. These corpuscles move with the velocity of light in a homogeneous medium in all possible directions in a straight line and they carry kinetic energy with them.

3. When these corpuscles fall on the retina of the eye, they produce the sensation of vision.

4. The size of corpuscles of different colors is different (ie, the color of light depends on the size of the corpuscle).

(A) Success of Carpuscles Theory

Based on this theory, the following facts related to light were explained successfully:

1. The light has energy: Since corpuscles have kinetic energy. Therefore, the energy of the light beam is due to the kinetic energy of the corpuscles.

2. Motion of light along a straight line: Since velocity of the corpuscle is very high, the effect of external forces on it is negligible. Therefore, it moves in a straight line.

3. Motion of light in vacuum: Corpuscles can move through vacuum.

4. Reflection of light: To explain the reflection of light, Newton assumed that when a corpuscle reaches close to a reflecting surface, then the surface repels it with a force whose direction is perpendicular to the surface and whose magnitude decreases sharply as the distance of corpuscles increases from the surface.

In Figure, let $PO$ be a reflecting surface and $P'Q'$ be an imaginary surface just above it at negligible height. When a light corpuscle moves towards the surface, then it moves along a straight line from $A$ to $B$ (since the force is zero). As it reaches the point $B$ of surface $PQ$, a repulsive force starts acting perpendicular to the surface (upward in the figure). Let $i$ is an angle of incidence at point $B$, then the velocity of the corpuscles at point $B$ has two components- component parallel to surface $V_{||} =v \: sin \: i$ and component perpendicular to surface $V_{|} = v \: cos \: i$. After crossing point $B$, the parallel component remains same but the perpendicular component decreases. At point $C$ of surface $PQ$, the perpendicular component becomes zero. After this direction of the perpendicular component changes and the corpuscles move along path CD. Beyond D again it moves along a straight line as the force becomes ineffective. If $r$ is the angle of reflection at point $D$, then the parallel component of velocity at $D$ will be $v\: sin\: r$. Since the parallel component remains constant. Therefore, comparing them at points $B$ and $D$.

$v \: sin \: i=v \: sin\: r$

$sin \: i= sin\: r$

$i=r$

i.e., the above equation shows that the incident angle and the reflected angle are equal. In the figure above, incident ray, reflected ray and normal all three are in the plane of paper. Therefore laws of reflection are verified.

5. Refraction of light: To explain the refraction of light, Newton considered two different situations :

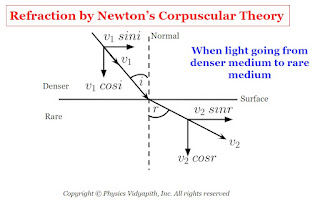
a.) When the light goes from a denser medium to a rare medium: In this condition when the corpuscle reaches near the surface, the surface exerts a normal repulsive force on it. As a result, the perpendicular component of velocity of the corpuscles decreases however it does not reduce to zero as in the case of refraction. Therefore, enters the second medium with a reduced perpendicular component and same constant value of the parallel component i.e., moves along a straight line bending away from normal.

If $i$ and $r$ are the angle of incidence and angle of refraction and $v_{1}$ and $v_{2}$ are the velocity of corpuscle in medium first and second medium. If the parallel component is constant,

$v_{1} \: sin \: i =v_{2} \: sin\: r$

$\frac{sin \: i}{sinr} =\frac{v_{2}}{v_{1}}$

From Figure

$i \lt r$

Therefore

$sin \: i \lt sin\: r$

$v_{2} \lt v_{1}$

Therefore, from the corpuscular theory, velocity light in a denser medium ($v_{1}$) is greater than the velocity light in a rare medium ($v_{2}$).

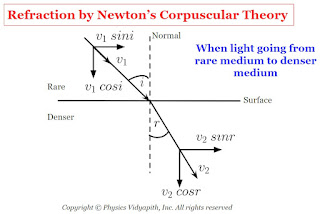
b.) When the light goes from a rare medium to a denser medium: In this condition when the corpuscle reaches near to the surface, the surface attracts it normally. As a result, the normal component of its velocity increases. Therefore, the corpuscular enters the second medium with an increased normal component and the same parallel component of velocity and moves along a straight line bending towards the normal. 

$v_{1} \: sin \: i =v_{2} \: sin\: r$

$\frac{sin \: i}{sinr} =\frac{v_{2}}{v_{1}}$

From Figure

$i \gt r$

Therefore

$ sin \: i \gt sin\: r$

$v_{2} \gt v_{1}$

Therefore, velocity light in a denser medium ($v_{1}$) is greater than the velocity light in a rare medium ($v_{2}$).

B) Failure of the Corpuscles Theory

The following are the main reasons for the failure of this theory:

1. Interference, diffraction, polarisation of light, and the photoelectric effect, etc. can not be explained using this principle. For example, in interference, when two light beams interfere, darkness is produced at the same places. It is not possible that two corpuscles destroy each other.

2. According to this theory, the velocity of light is greater in the denser medium as compared to the rare medium. But Focault's had proved experimentally that the velocity of light is less in denser mediums as compared to the velocity of light in rare mediums.

3. According to this theory, greater the temperature of the source greater the velocity of the corpuscles. Actually, the velocity of light does not depend on the temperature of the source.

4. According to this theory, the mass of the source should decrease as it continuously emits corpuscles but it does not happen in reality.

5. In this theory two opposite assumptions are considered to explain reflection and refraction. To explain reflection and refraction through denser to rarer, the repulsive force by the surface is assumed and to explain refraction from rare to denser, the force of attraction by the surface is assumed. These assumptions are opposite and they don't have any scientific base.

Read More

Nuclear force and its properties

Nuclear Force

A forces that act between the nucleons (i.e proton and neutron) inside the nucleus. This force is called the nuclear force.

These forces are responsible to keep the nucleons bound inside the nucleus.

Properties of Nuclear Force

There are the following properties of nuclear force is given below.

(i) These are strong nuclear forces otherwise protons cannot exist in the nucleus.

(ii) The intensity of these forces is very large. The intensity of nuclear force is maximum among, so far known forces.

(iii) It is not electrical in nature. If we assume them electrical forces, then the protons cannot reside in nucleus.

(iv) These forces do not depend on charge. The force acting between the nucleons (such as proton-proton, neutron-neutron and proton-neutron) is of same nature.

(v) These are not gravitational forces because the mass of the particles inside the nucleus is very small, while the magnitude of nuclear force is very large.

(vi) These forces are short range forces. They are confined inside the nucleus (i. e., $10^{-15} m$ equal to the diameter of nucleus). There is no existence of these forces outside the nucleus.

Read More

Limitations of Bohr's Model

Although Bohr's model of hydrogen atom and hyarogen like atom was successful in explaining the stability and spectrum even then it has few limitations. which are as follows:

(1) This model could not explain the spectrum of atom having more than one electron.

(2) This model could not explain the relative intensity of spectral lines. (i. e., few transitions are more acceptable than others why?)

(3) When a spectral line is observed by spectroscope of high resolution power, more than one lines are observed. This is known as fine structure of spectral line. Bohr model could not explain this.

(4) Splitting of spectral lines in external magnetic field (Zeeman's effect) and in external electric field (Stark's effect) could not be explained by this model.

(5) This model could not explain the distribution of electrons in different orbit.

Few limitations of Bohr's model are removed in Somer-field's model of atom. (In this model, the orbit of electron was considered as elliptical instead of circular ). But this model also has its limitations. Vector atomic model, which is based on quantum mechanics, explains clearly the structure of atom.

Read More

Comparison of Isothermal and Adiabatic Processes for an Ideal Gas

Isothermal Process:

1.) In this process temperature remains constant i.e.$(\Delta T= 0)$.

2.) In this process internal energy remains constant i.e. $(\Delta U= 0)$.

3.) This process takes place very slowly.

4.) In this process the system is surrounded by a perfectly conducting material, whose conductivity is infinite.

5.) This process obeys Boyle's law i.e. $(PV= constant)$.

6.) In this process the slope of isothermal curve $=-\frac{P}{V}$

7.) In this process specific heat of gas should be infinite.

Adiabatic Process:

1.) In this process exchange of heat does not take place i.e. $(\Delta Q= 0)$ but temperature changes.

2.) In this process internal energy changes.

3.) This process takes place very rapidly.

4.) In this process the system is surrounded by a perfectly insulating material, whose conductivity is zero.

5.) This process obeys Poisson's law i.e. $(PV^{\gamma} = constant)$.

6.) In this process the slope of adiabatic curve $=- \gamma \frac{P}{V}$

7.) In this process specific heat of gas should be zero.

Read More

Concept of Perfect Gas

Concept of Perfect (ideal) Gas:

An imaginary gas whose properties are similar to the properties of a real gas (a gas whose molecules occupy space and interact with each other) at infinitely low pressure. This imaginary gas is called 'perfect gas' or ideal gas'.

According to the definition, the following properties are imagined in a perfect gas :

(1) It strictly obeys Boyle's law, Charles' law, and the law of pressure under all conditions of temperature and pressure.

(2) Its pressure coefficient and volume coefficient are exactly equal to each other.

(2) Its molecules are infinitesimally small.

(3) There is no force of attraction between its molecules. Obviously, a perfect gas cannot be converted into a liquid or solid state, because a force of attraction is necessary between the molecules in the liquid or the solid state.

In practice, the gases that are difficult to liquefy, such as oxygen, nitrogen, hydrogen, and helium can be considered as perfect, although these are also not ideally perfect.

Read More

Failure of Wave Theory in Explaining Photoelectric Emission Effect

Description of failure of wave theory in explaining photoelectric effect:

Although reflection, refraction, interference, diffraction and polarisation etc. are explained on the basis of wave theory but the laws of photoelectric effect cannot be explained on the basis of the wave theory of light. There are three main reasons for failure:

1.) According to wave theory, as the intensity of incident light increases, incident energy also increases. Therefore, greater is the intensity, greater will be the energy absorbed by the electrons of metal and therefore greater should be the kinetic energy of photoelectrons. From experimental observations, it is clear that the maximum kinetic energy of photoelectrons does not depend on the intensity of incident light.

2.) According to wave theory, photoelectric emission should occur for all the frequencies provided that it has enough energy to emit the electrons from the metal. Although from experimental observation it is clear that if the frequency of incident light is less than the threshold frequency, photoelectrons are not emitted.

3.) The energy carried by the light waves is absorbed by all the electrons and not by a single electron. Therefore, if the intensity of light is less, for the emission of electrons, there should be some time to collect sufficient energy. Although it is clear from experimental observation, the electrons are emitted instantaneously, whatever small be the intensity of light.

Read More

Einstein Photoelectric Emission Effect Law

Description of the Light:

According to the Albert Einstein

The light is consist of small packets or bundles of energy. These packets are called photon. The energy of each photon is $h \nu$.

Theory of Photoelectric Effect:

When the photon of ultraviolet ray is incident on the metal then this energy is used in two parts:

1.) To emit the electron from a metal surface i.e. Work Function. The electron emitted from a metal surface is called the photoelectron.

2.) Remaining energy increases the kinetic energy of the emitted photoelectron. This is the maximum kinetic energy of the photoelectron.

Let us consider

The energy of incident Ultraviolet Photon $E=h\nu$

The work function $W= h \nu_{\circ}$

The maximum kinetic energy of photo electron $K_{max}= \frac{1}{2}mv^{2}_{max}$

According to Einstein's photoelectric effect theory

$E=W+K_{max}$

$h \nu = h \nu_{\circ} + \frac{1}{2}m v^{2}_{max}$

$h \nu - h \nu_{\circ} = \frac{1}{2}m v^{2}_{max}$

$h \left( \nu - \nu_{\circ} \right) = \frac{1}{2}m v^{2}_{max}$

Where
$\nu \rightarrow$ Frequency of incident Ultraviolet ray photon
$\nu_{\circ} \rightarrow$ Threshold frequency to emit the photoelectron from the metal surface
$ v_{max} \rightarrow$ Maximum velocity of emitted photoelectron from the metal surface

Read More

Laws of photoelectric emission

There are the following laws of photoelectric emission:

1.) The rate of emission of photoelectrons from the metal surface is directly proportional to the intensity of the incident light on the metal surface.

2.) The maximum kinetic energy of photoelectrons does not depend on the intensity of incident light.

3.) If the frequency of incident light is less than the threshold frequency then no photoelectrons will come out of the surface.

4.) If the frequency of incident light is equal to the threshold frequency then electrons will come out of the surface but the kinetic energy of emitted photoelectrons will be zero.

5.) As the frequency of incident light increases greater than the threshold frequency, the maximum kinetic energy $K_{max}$ of photoelectrons emitted from the metal surface also increases.

6.) The value of threshold frequency depends upon the nature of the metal surface and its value is different for different metals.

7.) There is no time lag in the emission of photoelectrons to the metal surface i.e., as the light of proper from frequency is made to the incident on the metal surface, photoelectrons immediately come out of the surface within no time.

Read More

Expression for fringe width in Young's double slit experiment

Expression for fringe's width:

Let us consider two wave from slit $S_{1}$ and $S_{2}$ superimpose on each other and form interfernece patteren on the screen. The distance between the two slits is $d$ and distance between slit to screen is $D$. Now take a $n^{th}$ fringe from the centre $O$ of the screen which is at distance $y_{n}$.

So the path difference between the rays

$\Delta x = S_{2}P- S_{1}P \quad(1)$

In $\Delta S_{1}PM$

$S_{1}P^{2}=S_{1}M^{2}+PM^{2} \quad(2)$

From figure:

$S_{1}M =D$
$PM= y_{n}- \left(\frac{d}{2}\right) $

Now subtitute these values in equation $(2)$, then

$S_{1}P^{2}=D^{2}+ \left( y_{n}- \frac{d}{2} \right)^{2} \quad(3)$

In $\Delta S_{2}PN$

$S_{2}P^{2}=S_{2}N^{2}+PN^{2} \quad(4)$

From figure:

$S_{2}N =D$
$PN= y_{n} + \left(\frac{d}{2}\right) $

Now subtitute these values in equation $(4)$, then

$S_{2}P^{2}=D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2} \quad(5)$

Now subtract the equation $(3)$ in equation $(5)$

$S_{2}P^{2} - S_{1}P^{2} = \left[D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2}\right] - \left[ D^{2}+ \left( y_{n}- \frac{d}{2} \right)^{2} \right] $

$S_{2}P^{2} - S_{1}P^{2} = D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2} - D^{2} - \left( y_{n}- \frac{d}{2} \right)^{2} $

$S_{2}P^{2} - S_{1}P^{2} = \left( y_{n} + \frac{d}{2} \right)^{2} - \left( y_{n}- \frac{d}{2} \right)^{2} $

$S_{2}P^{2} - S_{1}P^{2} = y^{2}_{n} + \left(\frac{d}{2}\right)^{2} +2 y_{n} \left(\frac{d}{2}\right) - y^{2}_{n} - \left(\frac{d}{2}\right)^{2} +2 y_{n} \left(\frac{d}{2}\right) $

$S_{2}P^{2} - S_{1}P^{2} = y^{2}_{n} + \left(\frac{d}{2}\right)^{2} + y_{n} d - y^{2}_{n} - \left(\frac{d}{2}\right)^{2} + y_{n} d $

$S_{2}P^{2} - S_{1}P^{2} = y_{n} d + y_{n} d $

$ \left( S_{2}P + S_{1}P \right) \left( S_{2}P - S_{1}P \right) = 2y_{n} d$

$ \left( S_{2}P + S_{1}P \right) \Delta x = 2y_{n} d \quad \left\{from \: equation\: (1)\right\} \qquad(6)$

In this experiment, the distance between slit and screen i.e. $D$ is much greater than the distance between the slit i.e. $d$ so angle $\theta$ will be very small. So from figure

$S_{1}P = S_{2}P = D$

Substitute this value in the equation $(6)$, therefore equation $(6)$ can be written as

$ 2D \Delta x = 2y_{n} d $

$D \Delta x = y_{n}$

$\Delta x = \frac{y_{n} d}{D} \quad (7) $

This is equation of path differnce between two wave from slit $S_{1}$ and slit $S_{2}$.

Condition For Bright Fringe:

The path difference for bright fringe is

$\Delta x= n \lambda \qquad(8)$

From equation $(7)$ and equation $(8)$

$n \lambda = \frac{ d}{D} $

$y_{n} = \frac{n \lambda D}{d} \quad(9)$

This is the equation for distance of $n^{th}$ bright fringe. Now the distance of $(n+1)^{th}$ bright fringe.

$y_{n+1} = \frac{\left( n+1 \right) \lambda D}{d} \quad(10)$

The dark fringe lie between the two consecutive bright fringe. So width of the dark fringe

$\beta = y_{n+1} - y_{n}$

Now subtitute the value of $y_{n+1}$ and $y_{n}$ in the above equation $(9)$ and equation $(10)$, then

$\beta = \frac{\left( n+1 \right) \lambda D}{d} - \frac{n \lambda D}{d}$

$\beta = \frac{\lambda D}{d} \quad(11)$

This is the equation of width of dark fringe.

Condition For Dark Fringe:

The path difference for dark fringe is

$\Delta x = (2n-1) \lambda \quad(12)$

From equation $(7)$ and equation $(12)$

$ (2n-1) \lambda = \frac{y_{n} d}{D} $

$y_{n} = \frac{(2n-1) \lambda D}{d} \quad(13)$

This is the equation for distance of $n^{th}$ dark fringe. Now the distance of $(n+1)^{th}$ dark fringe.

$y_{n+1} = \frac{\left[ 2 (n+1)-1) \right] \lambda D}{d} $

$y_{n+1} = \frac{(2n+1)\lambda D}{d} \quad(14)$

The bright fringe lie between the two consecutive dark fringe. So width of the bright fringe

$\beta = y_{n+1} - y_{n}$

Now subtitute the value of $y_{n+1}$ and $y_{n}$ in the above equation $(13)$ and equation $(14)$, then

$\beta = \frac{(2n+1)\lambda D}{d} - \frac{(2n-1) \lambda D}{d}$

$\beta = \frac{\lambda D}{d} \quad(15)$

This is the equation of width of bright fringe.

The equation $(11)$ and equation $(15)$ shows that the width of bright fring and dark fringe is same.

Alternative method to find the path differnce of two wave in Young's double-slit Experiment

Let us consider: Two wave from slit $S_{1}$ and $S_{2}$ superimpose on each other and form interfernece patteren on the screen.

The distance between the two slits is $\rightarrow d$

The distance between slit to screen is $\rightarrow D$

The distance of $n^{th}$ fringe from the centre $O$ of the screen is $\rightarrow y_{n}$.

So the path difference between the two rays is

$\Delta x = S_{2}M \quad(1)$

Now from figure, In $\Delta S_{1}S_{2}M$

$sin \theta = \frac{S_{2}M}{S_{1}S_{2}} \quad(2)$

In $\Delta PNO$

$tan \theta = \frac{PO}{NO} \quad(3)$

The distance between slit and screen i.e. $D$ is much greater than the distance between the slit i.e. $d$ so angle $\theta$ will be very small i.e. $sin \theta \approx tan \theta \approx \theta $. Now equate the equation $(2)$ and equation $(3)$

$\frac{PO}{NO} = \frac{S_{2}M}{S_{1}S_{2}} \quad(4)$

Now the value from the above figure

$\frac{y_{n}}{D} = \frac{\Delta x}{d} $

$\Delta x = \frac{y_{n} d}{D} $

This is the equation of the path difference between two wave from slit $S_{1}$ and $S_{2}$.

Now the derivation for the condition for Bright and Dark fringe can be used here as it is given above.

Read More

Analytical expression of intensity for constructive and destructive interference due to Young's double slit

Analytical expression of intensity for interference due to Young's double slit:

Let us consider two waves from slit $S_{1}$ and $S_{2}$ having amplitude $a_{1}$ and $a_{2}$ respectively superimpose on each other at point $P$ . If the displacement of waves is $y_{1}$ and $y_{2}$ and the phase difference is $\phi$ then

$y_{1}=a_{1} \: sin \omega t \qquad(1)$

$y_{2}=a_{2} \: sin \left( \omega t + \phi \right) \qquad(2)$

According to the principle of superposition:

$y=y_{1}+y_{2} \qquad(3)$

Now substitute the value of $y_{1}$ and $y_{2}$ in the above equation $(3)$

$y=a_{1} \: sin \omega t + a_{2} \: sin \left( \omega t + \phi \right)$

$y=a_{1} \: sin \omega t + a_{2} \left( sin \omega t \: cos \phi + cos \omega t \: sin \phi \right) $

$y=a_{1} \: sin \omega t + a_{2} \: sin \omega t \: cos \phi + a_{2}\: cos \omega t \: sin \phi $

$y= \left( a_{1} + a_{2} \: cos \phi \right) \: sin \omega t + a_{2} \: sin \phi \: cos \omega t \qquad(4)$

Let

$a_{1} + a_{2} \: cos \phi = A\: cos\theta \qquad(5)$

$a_{2} \: sin \phi = A\: sin\theta \qquad(6)$

Now the above equation $(4)$ can be written as

$y= A\: cos\theta \: sin \omega t + A\: sin\theta \: cos \omega t $

$y= A \left( cos\theta \: sin \omega t + sin\theta \: cos \omega t \right)$

$y= A \: sin \left( \omega t + \theta \right) \qquad(7)$

This is the equation of the resultant displacement of the waves from slit $S_{1}$ and $S_{2}$ at point $P$ on the screen.

Now square the equation $(5)$ and equation $(6)$ and then add to them so

$ A^{2} \: sin^{2}\theta + A^{2}\: cos^{2}\theta = \left( a_{1} + a_{2} \: cos \phi \right)^{2} + a^{2}_{2} \: sin^{2} \phi $

$ A^{2} \left( sin^{2}\theta + cos^{2}\theta \right) = a^{2}_{1} + a^{2}_{2} \: cos^{2} \phi + 2a_{1} \: a_{2} \: cos\phi + a^{2}_{2} \: sin^{2} \phi $

$ A^{2} = a^{2}_{1} + a^{2}_{2} \left( cos^{2}\phi + sin^{2}\phi \right) + 2a_{1} \: a_{2} \: cos\phi $

$ A^{2} = a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi \qquad(8)$

$ A = \sqrt{ a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi }\qquad(9)$

Resultant Intensity:

The resultant intensity at point $P$ due waves from slit $S_{1}$ and $S_{2}$ can be find by flollowing formula:

$I=A^{2}$

Now subtitute the va;ue of $A^{2}$ from equation $(8)$ in the above equation

$I= a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi \qquad(10)$

$I= I_{1} + I_{2} + 2\sqrt{I_{1} \: I_{2}} \: cos\phi \qquad(11)$

Constructive Interference:

For constructive interference the $cos\phi$ should be equal to +1 i.e. $cos\phi =1$

Phase Difference in Constructive Interference:

We know that for constructive interference $cos\phi =1$

$cos\phi = cos( 2n\pi)$

$\phi = 2n\pi \qquad(12)$

Path difference in Constructive Interference:

We know that the path difference

$\Delta x = \frac{\lambda}{2 \pi} \phi$

Now subtitute the value of $\phi $ from equation $(12)$ in the above equation

$\Delta x = \frac{\lambda}{2 \pi} 2n\pi$

$\Delta x = n \lambda \qquad(13)$

Resultant Amplitude due to Constructive Interference:

For constructive interference, the resultant amplitude is maximum at point $P$. So from equation $(9)$

$ A_{max} = \sqrt{ a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} } \qquad \left( \because cos\phi =+1 \right)$

$ A_{max} = \sqrt{ \left (a_{1} + a_{2} \right)^{2}} $

$ A_{max} = \left( a_{1} + a_{2} \right) \qquad(14)$

For constructive interference, the resultant amplitude of the waves is the sum of the amplitude of individual waves.

Resultant Intensity due to Constructive Interference:

For constructive interference, the resultant intensity is maximum at point $P$. So from equation $(10)$

$I_{max}= a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \qquad \left( \because cos\phi =+1 \right)$

$I_{max}=\left( a_{1} + a_{2} \right)^{2} \qquad(15)$

From equation $(11)$

$I_{max}= I_{1} + I_{2} + 2\sqrt{I_{1} \: I_{2}} \qquad(16)$

Destructive Interference:

For destructive interference the $cos\phi$ should be equal to -1 i.e. $cos\phi = -1$

Phase Difference in Destructive Interference:

We know that for destructive interference $cos\phi = -1$

$cos\phi = cos \left( \left( 2n \pm 1 \right)\pi \right)$

$\phi = \left( 2n \pm 1 \right)\pi \qquad(17)$

Path difference in Destructive Interference:

We know that the path difference

$\Delta x = \frac{\lambda}{2 \pi} \phi$

Now subtitute the value of $\phi $ from equation $(17)$ in the above equation

$\Delta x = \frac{\lambda}{2 \pi} \left( 2n \pm 1 \right)\pi$

$\Delta x = \left( 2n \pm 1 \right) \frac{\lambda}{2} \qquad(18)$

Resultant Amplitude due to Destructive Interference:

For the destructive interference, the resultant amplitude is minimum at point $P$. So from equation $(9)$

$ A_{min} = \sqrt{ a^{2}_{1} + a^{2}_{2} - 2a_{1} \: a_{2} } \qquad \left( \because cos\phi =-1 \right)$

$ A_{min} = \sqrt{ \left (a_{1} - a_{2} \right)^{2}} $

$ A_{min} = \left( a_{1} - a_{2} \right)$

For constructive interference, the resultant amplitude of the waves is the difference in amplitude of individual waves.

Resultant Intensity due to Destructive Interference:

For the destructive interference, the resultant intensity is minimum at point $P$. So from equation $(10)$

$I_{min}= a^{2}_{1} + a^{2}_{2} - 2a_{1} \: a_{2} \qquad \left( \because cos\phi =-1 \right)$

$I_{min}=\left( a_{1} - a_{2} \right)^{2}$

From equation $(11)$

$I_{min}= I_{1} + I_{2} - 2\sqrt{I_{1} \: I_{2}} $

Read More