Derivation of Lorentz Transformation's Equations

Derivation:

Let us consider two inertial frames $S$ and $S'$ in which frame $S'$ is moving with constant velocity $v$ along the positive x-axis direction relative to the frame $S$. Let $t$ and $t'$ be the time recorded in two frames. Let the origin $O$ and $O'$ of the two reference systems coincide at $t=t'=0$.

Now suppose, a source of light is situated at the origin $O$ in the frame $S$, from which a wavefront of light is emitted at time $t=0$. When the light reaches point $P$, the time required by a light signal in travelling the distance OP in the Frame $S$ is

$ t=\frac{OP}{c}$

$ t=\frac{\left (x^{2}+y^{2}+z^{2} \right )}{c}$

$ x^{2}+y^{2}+z^{2}=c^{2}t^{2}\qquad (1)$

The equation $(1)$ represents the equation of wavefront in frame $S$. According to the special theory of relativity, the velocity of light will be $c$ in the second frame $S'$. Hence in frame $S'$ the time required by the light signal in travelling the distance $O'P$ is given by

$ t'=\frac{O'P}{c}$

$ x'^{2}+y'^{2}+z'^{2}=c^{2}t^{2}\qquad (2)$

According to the Galilean transformation equation:

$ \begin{Bmatrix} x'=x-vt\\ y'=y\\ z'=z\\ t'=t \end{Bmatrix}$

Now substitute these values in equation $(2)$ then we get

$ (x-vt)^{2}+y^{2}+z^{2}=c^{2}t^{2}$

$ x^{2}+v^{2}t^{2}-2xvt+y^{2}+z^{2}-c^{2}t^{2}=0$

The above equation is certainly not same as the equation $(1)$ because it contains an extra term $(-2xvt+v^{2}t^{2})$. Thus the Galilean transformation fails.

Further $t=t'$ because $\left( t=\frac{OP}{c} \: and \: t'=\frac{O'P}{c} \right)$ which does not agree with Galilean transformation equations.

The extra term $(-2xvt+v^{2}t^{2})$ indicates that transformations in $x$ and $t$ should be modified so that this extra term is cancelled. So modification in transformation

$ x'=\alpha (x-vt) \quad for \: x'=0,\: x=vt$

$ t'=\alpha (t+fx)$

Where $α$, $α'$ and $f$ are constant to be determined for Galilean Transformations $α= α'=1$ and $f=0$. Now substituting these modified values in equation $(2)$ so

$ \alpha ^{2}(x-vt)^{2}+y^{2}+z^{2}=c^{2}\alpha'^{2}(t+fx)^{2}$

$ \alpha ^{2}(x^{2}+v^{2}t^{2}-2xvt)+y^{2}+ z^{2} =c^{2}\alpha{'}^{2}(t^{2}+f^{2}x^{2}+2fxt)$

$\alpha^{2}x^{2}+\alpha^{2}v^{2}t^{2}-2xvt\alpha^{2}+y^{2}+ z^{2} =c^{2} \alpha'^{2}t^{2}+c^{2} \alpha'^{2}f^{2}x^{2}+c^{2} \alpha'^{2}(2fxt)$

$ x^{2}(\alpha^{2}-c^{2} \alpha'^{2}f^{2})- 2xt(v\alpha^{2}+c^{2}\alpha '^{2}f)+y^{2}+ z^{2} =c^{2}t^{2}\left ( \alpha'^{2}-\frac{\alpha ^{2}v^{2}}{c^{2}} \right )\qquad(3)$

This result obtained from applying transformations from frame $S'$ to $S$ must be identical to equation $(1)$. Therefore

$ \alpha ^{2}-c^{2}\alpha '^{2}f^{2}=1\qquad (i)$

$ v\alpha ^{2}+c^{2}\alpha '^{2}f=0\qquad (ii)$

$ \alpha '^{2}-\frac{\alpha ^{2}v^{2}}{c^{2}}=1\qquad (iii)$

After solving equation $(i)$ equation $(ii)$ and equation $(iii)$, we get

$ \alpha =\alpha '=\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$ $ f=-\frac{v}{c^{2}}$

Thus, The new transformation equation is invariant at the velocity of light $c$. These are:

$ \begin{Bmatrix} x'=\frac{x-vt}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\\ y'=y\\ z'=z\\ t'=\frac{(t-\frac{vx}{c^{2}})}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \end{Bmatrix}$

These equations are called Lorentz Transformations because they were first obtained by Dutch Physicist H. Lorentz.

The above transformation equation shows that frame $S'$ is moving in positive x-direction with velocity $v$ relative to the frame $S$. But if we say that frame $S$ is moving with $v$ velocity relative to frame $S'$ along negative x-direction then the transformation is:

$ \begin{Bmatrix} x=\frac{x'+vt'}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\\ y=y'\\ z=z'\\ t=\frac{(t'+\frac{vx'}{c^{2}})}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \end{Bmatrix}$

These are known as inverse Lorentz Transformations equations.

Read More

Force between multiple charges (Superposition principle of electrostatic forces)

Principle of Superposition for Electric force:

If a system contains a number of interacting charges, then the net force on anyone charge equals the vector sum of all the forces exerted on it by all the other charges. This is the principle of Superposition for electric force.

If a system contains n point charges $ q_{1},q_{2},q_{3}........q_{n}$. Then according to the principle of superposition, the force acting on the charge $q_{1}$ due to all the other charges

$\overrightarrow{F_{1}}=\overrightarrow{F_{12}}+\overrightarrow{F_{13}}+\overrightarrow{F_{14}}+...+\overrightarrow{F_{1n}} \qquad (1)$

Where $\overrightarrow{F_{12}}$ is the force on charge $q_{1}$ due to charge $q_{2}$, $\overrightarrow{F_{13}}$ that is due to $q_{3}$ and $\overrightarrow{F_{1n}}$ that due to $q_{n}$.

If the distance between the charges $q_{1}$ and $q_{2}$ is $\widehat{r}_{12}$ (magnitude only) and $\widehat{r}_{21}$ is unit vector from charge $q_{2}$ to $q_{1}$, then

$\overrightarrow{F_{12}}=\frac{1}{4\pi \epsilon _{0}}\frac{q_{1}q_{2}}{r_{12}^{2}}\:\hat{r_{21}} \qquad (2)$

Similarly, the forces on charge $q_{1}$ due to other charges are given by

$ \overrightarrow{F_{13}}=\frac{1}{4\pi \epsilon _{0}}\:\frac{q_{1}q_{3}}{r_{13}^{2}}\:\hat{r_{31}}\qquad (3)$

$.............................$

$.............................$

$ \overrightarrow{F_{1n}}=\frac{1}{4\pi \epsilon _{0}}\:\frac{q_{1}q_{n}}{r_{1n}^{2}}\:\hat{r_{n1}}\qquad (n)$

Hence, putting the value of $\overrightarrow{F_{12}},\overrightarrow{F_{13}},\overrightarrow{F_{14}}......\overrightarrow{F_{1n}}$, in equation $(1)$, the total force on charge $q_{1}$ due to all other charges is given by

$ \overrightarrow{F_{1}}=\frac{1}{4\pi \epsilon _{0}}[\:\frac{q_{1}q_{2}}{r_{12}^{2}}\:\hat{r_{21}}+\frac{q_{1}q_{3}}{r_{13}^{2}}\:\hat{r_{31}}+....\\ \quad\quad\quad ..+\frac{q_{1}q_{n}}{r_{1n}^{2}}\:\hat{r_{n1}}]$

The same procedure can be applied to finding the force on any other charge due to all the remaining charges. For example, the force on $q_{2}$ due to all the other charges is given by

$ \overrightarrow{F_{2}}=\frac{1}{4\pi \epsilon _{0}}[\:\frac{q_{2}q_{1}}{r_{21}^{2}}\:\hat{r_{12}}+\frac{q_{2}q_{3}}{r_{23}^{2}}\:\hat{r_{32}}+... \\ \quad\quad\quad ..+\frac{q_{2}q_{n}}{r_{2n}^{2}}\:\hat{r_{n2}}\:]$

Some Observations Points of Coulomb's Law:

There are the following point has been observed in Coulomb's law, that are

1. Coulomb's force between the two charges is directly proportional to the product of the magnitude of the charge.
   
   
   $ F\propto q_{1}q_{2}$


2. Coulomb's force between the two charges is inversely proportional to the square of the distance between the two charges.
   
   
   $F\propto \frac{1}{r^{2}}$


3. The electrostatic force acts between the line joining the charges. In two charges, one charge is assumed to be at rest for the calculation of the force on the second charge. So It is also known as a central force.


4. The magnitude of the electrostatic force is equal and the direction of force is opposite. So the electrostatic force is also known as the action and reaction pair.


5. The electrostatic force between two charge does not affect by the presence and absence of any other charges but the net force increase on the source charge.

Read More

Definition and derivation of the phase velocity and group velocity of wave

Wave:

A wave is defined as a disturbance in a medium from an equilibrium condition that propagates from one region of the medium to other regions.

When such type of wave propagates in the medium a progressive change in phase takes place from one particle to the next particle.

Propagation of Wave: Wave propagation in the medium occurs with two different kinds of velocity. i.e. phase velocity and group velocity.

1. Phase Velocity:

The velocity with which plane of constant the phase of a wave propagates through the medium at a certain frequency is called the phase velocity or wave velocity.

A plane wave traveling in the positive x-direction is represented by

$y=A \: sin \omega (t-\frac{x}{v})$

Where $ \omega $ – angular frequency

$y=A \: sin(\omega t-\frac{\omega x}{v})$

$y=A \: sin(\omega t-kt) \qquad(1)$

For plane-wave $(\omega t-kx)$ is the phase of wave motion. For the plane of constant phase (wavefront). We have

$( \omega t-kx) = constant (\phi) \qquad(2)$

Differentiate with respect to time $(t)$ of the above equation

$ \omega -k.\frac{dx}{dt}=0$

$\frac{dx}{dt}=\frac{ \omega}{k}\qquad(3)$

$V_{p}=\frac{ \omega}{k} \qquad \left [ \because V_{p}= \frac{dx}{dt} \right ]$

Where $V_{p}$ - Phase Velocity of a wave

Question- Show that the phase velocity of matter-wave always exceeds the velocity of light.

Answer- Method-I

$V_{p}=\frac{ \omega }{k}$

$V_{p}=\frac{2\pi \nu }{\frac{2\pi }{\lambda }}$

$V_{p} = \frac{2 \pi h \nu}{\frac{2 \pi h}{\lambda }}$

$V_{P} = \frac{E}{P}$

$V_{P} =\frac{mc^{2}}{mv}$

$V_{P} =\frac{c^{2}}{v}$

Method-II:

$V_{P}=\nu \lambda$

$V_{P}=\frac{mc^{2}}{h} \frac{h}{mv}$

$V_{P}=\frac{c^{2}}{v}$

Where $v$ is the velocity of matter particles.

Wave packet→

A wave packet is an envelope or packet which contains the number of plane waves having different wavelengths or wavenumbers. These numbers of waves superimpose on each other and form constructive and destructive interference over a small region of space and a resultant wave obtain. The spread of amplitude of the resultant wave with distance determines the size of the wave packet. A wave packet is also called a wave group.

Group Velocity→

The velocity of propagation of wave packet through space is known as group velocity.

Group Velocity also represents the velocity of energy flow or transmission of information in a traveling wave or wave packet. It is represented by $V_{g}$. So

$V_{g} = \frac{d\omega }{dk}$

Expression for group velocity $(V_{g})$→

Let two plane simple harmonic waves of the same amplitude and slightly different wavelength traveling simultaneously in the positive x-direction in a dispersive medium be represented by –

$y_{1} = A\: sin{(\omega t-kx)} \qquad (1)$

$y_{2}= A\:sin[(\omega +\delta \omega )t-(k+\delta k)x] \qquad (2)$

From the superposition principle the resultant displacement of waves

$y=y_{1}+y_{2}\qquad (3)$

$y=A \: sin(\omega t-kx)+ A \: sin[(\omega +\delta \omega)t-(k+\delta k)x]$

$y=A[sin(\omega t-kx)+ sin{(\omega +\delta \omega )t-(k+\delta k )x}]$

$y=2Asin(\omega t-kx)cos\frac{1}{2}(t\delta \omega –x\delta k) \qquad (4)$

This is the analytical equation for the group of waves. This equation represents the following points –

1. The sine factors represent a carrier wave that travels with the phase velocity.


2. The amplitude of the resultant wave is

$R=2A cos \frac{1}{2}(t \delta\omega-x \delta k) \qquad (5)$

(A) For maximum amplitude→

$ cos\frac{1}{2}(\delta\omega t-x\delta k)=1 \qquad (6) $

Then the resultant amplitude of the wave packet will be

$R_{m}=2A \qquad $ {from equation $(5)$ }

Where $R_{m}$ - Resultant maximum amplitude

From equation$(6)$-

$cos\frac{1}{2}(t\delta\omega –x\delta k)=1$

$cos\frac{1}{2}(t\delta\omega –x\delta k)=cos0$

$\frac{1}{2}(t\delta\omega –x\delta k)=0$

$\frac{x}{t}=\frac{\delta\omega }{\delta k}$

$V_{g}=\frac{\delta\omega }{\delta k}$

OR

$V_{g}=\frac{d\omega}{dk}$

Thus maximum amplitude i.e. the center of the wave packet moves with velocity $\frac {d\omega}{dk}$ or group velocity.

(B) For minimum amplitude→

Let a wave packet that has minimum (zero) amplitude on two successive points $x_{1}and x_{2}$. So for minimum amplitude at point $x_{1}$ –

$cos\frac{1}{2}(t.\delta \omega –x_{1}.\delta k)=0$

$cos\frac{1}{2}(t.\delta \omega –x_{1}.\delta k)=cos(2n+1)\frac{\pi }{2}$

$\frac{1}{2}(t.\delta \omega –x_{1}.\delta k)=(2n+1)\frac{\pi }{2}$

$t.\delta \omega – x_{1}.\delta k=(2n+1)\pi \qquad(1)$

Similarly minimum amplitude at the second successive point $x_{2}$-

$t\delta \omega –x_{2}.\delta k =(2n-1)\pi \qquad(2)$

Now subtract the equation $(2)$ in equation $(1)$

$(t.\delta \omega – x_{1}.\delta k) – (t.\delta \omega - x_{2}.\delta k)= (2n+1)\pi–(2n-1)\pi $

$(x_{2}-x_{1}).\delta k=2\pi$

$x_{2}-x_{1}=\frac{2\pi}{\delta k}$

$x_{2}-x_{1}=\frac{2\pi}{d(\frac{2\pi}{\lambda})} $

$\delta x=\frac{-\lambda ^{2}}{\delta  \lambda }$

Here $\delta x$ -Length of the wave packet

The above equation also can be written as-

$ dx=\frac{-\lambda^{2}}{d \lambda }$

Prove that→

$V_{g}= -\lambda^{2} \frac{d\nu }{d\lambda}$

Where $\nu $ is the frequency and $\lambda $ is the wavelength.

Proof:

We know that

$V_{g}=\frac{d\omega }{dk}$

$V_{g}=\frac{d(2\pi\nu )}{d(\frac{2\pi }{\lambda })} \qquad \left( \because \omega= 2\pi \nu \: and \: k=\frac{2\pi}{\lambda } \right)$

$V_{g}=\frac{2\pi d\nu }{2\pi d( \frac{1}{ \lambda })}$

$V_{g}=-\lambda ^{2}\frac{d\nu }{d\lambda }$

Note: A moving particle cannot be equal to a single wave train. The speed of a single wave train is called the phase velocity so moving particles are equivalent to a group of waves or wave packets.

Read More

Product of phase velocity and group velocity is equal to square of speed of light

Prove that $\rightarrow$

The Product of phase velocity and group velocity is equal to the square of the speed of light i.e. $\left( V_{p}.V_{g}=c^{2} \right)$

Proof → We know that

$V_{p}=\nu \lambda \qquad(1)$

And de Broglie wavelength-

$\lambda =\frac{h }{mv}\qquad(2)$

According to Einstein's mass-energy relation-

$E=mc^{2}$

$h\nu=mc^{2}$

$\nu=\frac{mc^{2}}{h}\qquad(3)$

Now put the value of $\lambda $ and $\nu $ in equation$(1)$

$V_{p}= [\frac{mc^{2}}{h}] [\frac{h}{mv}]$

$V_{p}=\frac{C^{2}}{v}$

Since group velocity is equal to particle velocity i.e. $V_{g}=v$. So above equation can be written as

$V_{p}=\frac{C^{2}}{V_{g}}$

$V_{p}.V_{g}=C^{2}$

Note →

➢ $V_{g}=V_{p}$ for a non-dispersive medium ( in a non-dispersive medium all the waves travel with phase velocity).

➢ $V_{g}< V_{p}$ for normal dispersive medium

➢ $V_{g}> V_{p}$ for anomalous dispersive media.

Dispersive medium → The medium in which the phase velocity varies with wavelength or frequency is called a dispersive medium. In such a medium, waves of different wavelengths travel with different phase velocities.

Non-dispersive medium → The medium in which the phase velocity does not vary with wavelength or frequency is called a Non-dispersive medium.

Dispersive waves → Those waves in the medium for which phase velocity varies with wavelength or frequency are called dispersive waves.

Non-dispersive waves → Those waves in which phase velocity does not vary with wavelength are called non-dispersive waves. So phase velocity independent of wavelength.

Read More

Energy distribution spectrum of black body radiation

Description→ The energy distribution among the different wavelengths in the spectrum of black body radiation was studied by Lummer and Pringsheim in 1899. There are the following important observations of the study.

1. The energy distribution in the radiation spectrum of the black body is not uniform. As the temperature of the body rises the intensity of radiation for each wavelength increases.


2. At a given temperature, the intensity of radiation increases with increases in wavelength and becomes maximum at a particular wavelength with further in increases wavelength the intensity of radiation decreases.





Energy distribution in the spectrum of black body radiation

3. The points of maximum energy shift towards the shorter wavelength as the temperature increases i.e. $\lambda _{m} \times T=constant$. It is also known as Wein’s displacement law of energy distribution.


4. For a given temperature the total energy of radiation is represented by the area between the curve and the horizontal axis and the area increases with increases of temperature, being directly proportional to the fourth power of absolute temperatures.

   The total amount of heat radiated by a perfectly black body per unit area per unit time is directly proportional to the fourth power of its absolute temperature $(T)$.

   
   

   $E = \sigma T^{4}$

   
   
   Where $\sigma$ = Stefan constant having value $\left ({5}\cdot{67}\times{10}^{-8}Wm^{-2}K^{4}\right )$
   
   
   This is called Stefan-Boltzmann's law of energy distribution.

Read More

Derivation of torque on an electric dipole in an uniform and a non-uniform electric field

Torque on an electric dipole in a uniform electric field: Let us consider, An electric dipole AB, made up of two charges $+q$ and $-q$, is placed at a very small distance $2l$ in a uniform electric field $\overrightarrow{E}$. If $\theta$ is the angle between electric field intensity $\overrightarrow{E}$ and electric dipole moment $\overrightarrow{p}$ then the magnitude of electric dipole moment →

$\overrightarrow{p}=q\times\overrightarrow{2l}\qquad(1)$

Force exerted on charge $+q$ by electric field $\overrightarrow{E}$ →

$\overrightarrow{F_{+q}}=q\overrightarrow{E}\qquad(2)$

Here in the above equation(2), the direction of $\overrightarrow{F_{+q}}$ is along the direction of $\overrightarrow{E}$

Force exerted on charge $-q$ by electric field $\overrightarrow{E}$ →

$\overrightarrow{F_{-q}}= q\overrightarrow{E}\qquad(3)$

Here in the above equation(3) the direction of $\overrightarrow{F_{-q}}$ is in the opposite direction of $\overrightarrow{E}$

So, the net force of on an electric dipole→

$\overrightarrow{F}=\overrightarrow{F_{+q}} - \overrightarrow{F_{-q}}\qquad (4)$

Now substitute the value of equation $(2)$ and equation $(3)$ in above equation $(4)$. So net force→

$\overrightarrow{F}=0\qquad (5)$

Torque on electric dipole

Hence, the net translating force on an electric dipole in a uniform electric field is zero. But these two force is equal in magnitude, opposite in direction, and act at different point of the dipole so these force form a coupling force that exerts a torque on an electric dipole→

Torque = force x Perpendicular distance between the two forces

$\overrightarrow{\tau}=(qE).2l\:sin\theta\quad\quad\quad\quad(6)$

$ \overrightarrow{\tau}=pE\:sin\theta$

$\overrightarrow{\tau}=\overrightarrow{p}\times\overrightarrow{E}$

Case(I)→ If the dipole is placed perpendicular to the electric field i.e. $\theta=90^{\circ}$, the torque acting on it will be maximum. i.e.

$ \tau_{max}=pE $

Case(II)→ If the dipole is placed parallel to the electric field i.e. $\theta=0^{\circ}$ or $\theta=180^{\circ}$, the torque acting on it will be minimum. i.e.

$ \tau_{min}=0$

Direction of torque

Electric Dipole Moment:

We know that the torque

$ \overrightarrow{\tau}=pE\:sin\theta$

If $E=1$ and $\theta=90^{\circ}$ Then

$ \tau_{max} =p$

Hence Electric dipole moment is the torque acting on the dipole placed perpendicular to the direction of uniform electric field intensity.

Torque on an electric dipole in a non-uniform electric field:

In a non-uniform electric field, the $+q$ and $-q$ charges of a dipole experience different forces (not equal in magnitude and opposite in direction) at a slightly different position in the electric field, and hence a net force $\overrightarrow{F}$ act on the dipole in a non-uniform field. A net torque acts on the dipole which depends on the location of the dipole in the non-uniform field.

$\overrightarrow{\tau}=\overrightarrow{p}\times\overrightarrow{E}(\overrightarrow{r})$

Where $\overrightarrow{r}$ is the position vector of the center of the dipole.

When p and E are Parallel

In the non-uniform field, If the direction of the dipole moment $\overrightarrow{p}$ is parallel to electric field intensity $\overrightarrow{E}$ or antiparallel to electric field intensity $\overrightarrow{E}$ the net torque on the dipole is zero because the force on charges becomes linear.

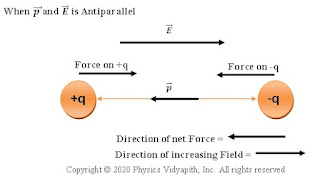When p and E are antiparallel

However, If $\overrightarrow{p}$ is parallel to $\overrightarrow{E}$, a net force on the dipole in the direction of increasing $\overrightarrow{E}$. When $\overrightarrow{p}$ is antiparallel to $\overrightarrow{E}$, a net force on the dipole in the direction of decreasing $\overrightarrow{E}$. As shown in the figure above.

Read More

Electric Dipole and Derivation of Electric field intensity at different points of an electric dipole

Electric Dipole:

An electric dipole is a system in which two equal magnitude and opposite point charged particles are placed at a very short distance apart.

Electric Dipole Moment:

The product of magnitude of one point charged particle and the distance between the charges is called the 'electric dipole moment'. It is vector quantity and the direction of electric dipole moment is along the axis of the dipole pointing from negative charge to positive charge.

Electric Dipole

Let us consider, the two charged particle, which has equal magnitude $+q$ coulomb and $-q$ coulomb is placed at a distance of $2l$ in a dipole so the electric dipole moment is →

$\overrightarrow{p}=q\times \overrightarrow{2l}$

Unit: $C-m$ Or $Ampere-metre-sec$

Dimension: $[ALT]$

Electric field intensity due to an Electric Dipole:

The electric field intensity due to an electric dipole can be measured at three different points:

1. Electric field intensity at any point on the axis of an electric dipole


2. Electric field intensity at any point on the equatorial line of an electric dipole


3. Electric field intensity at any point on an electric dipole

1. Electric field intensity at any point on the axis of an electric dipole:

Let us consider, An electric dipole $AB$ made up of two charges of $-q$ and $+q$ coulomb are placed in a vacuum or air at a very small distance of $2l$. Let a point $P$ be on the axis of an electric dipole and place it at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric field intensity due to dipole's charge.

Electric field intensity at any point on the axis of an electric dipole

So, Electric field intensity (magnitude only) at point $P$ due $+q$ charge of electric dipole

$ E_{+q}=\frac{1}{4\pi\epsilon}\frac{q}{(r-l)^{2}} \qquad(1)$

Electric field intensity (magnitude only) at point $P$ due $-q$ charge of electric dipole

$ E_{-q}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{(r+l)^{2}} \qquad(2)$

The net electric field at point $P$ due to an electric dipole

$ E=E_{+q}-E_{-q}\qquad(3)$

Subtitute the value of $E_{+q}$ and $E_{-q}$ in equation $(3)$, Then the above equation $(3)$ can also be written as follows

$E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{1}{(r-l)^{2}}-\frac{1}{(r+l)^{2}} \right ]$

$ E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{(r+l)^{2}-(r-l)^{2}}{(r+l)^{2}(r-l)^{2}} \right ]$

$ E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{(r^{2}+l^{2}+2lr-r^{2}-l^{2}+2lr)}{(r+l)^{2}(r-l)^{2}} \right ]$

$ E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{4rl}{(r^{2}-l^{2})^{2}} \right ]\qquad(4)$

Here $l \lt r $ so $l^{2} \lt \lt r^{2}$ therefore neglect the term $l^{2}$ in above equation $(4)$ so we can write above equation

$ E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{4rl}{(r^{2})^{2}} \right ]$

$E=\frac{1}{4\pi\epsilon _{0}}\left [ \frac{2p}{r^{3}} \right ]\qquad (5)$

This is the equation of electric field intensity at a point on the axis of an electric dipole.

The vector form of the above equation $(5)$ is

$\overrightarrow{E}=\frac{1}{4\pi\epsilon _{0}}\left [ \frac{2\overrightarrow{p}}{r^{3}} \right ]$

2. Electric field intensity at any point on the equatorial line of an electric dipole:

Let us consider, An electric dipole $AB$ made up of two charges of $+q$ and $-q$ coulomb are placed in vacuum or air at a very small distance $2l$. Let a point $P$ be on the equatorial line of an electric dipole and place it at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric field intensity due to dipole's charge.

So, Electric field intensity (magnitude only) at point $P$ due $+q$ charge of electric dipole

Electric field intensity at a point of the equatorial line of an electric dipole

$E_{+q}=\frac{1}{4\pi\epsilon_{0}}\left [\frac{q}{(r^{2}+l^{2})} \right ] \qquad(1)$

Electric field intensity (magnitude only) at point $P$ due to $-q$ charge of electric dipole

$E_{-q}=\frac{1}{4\pi\epsilon_{0}}\left [\frac{q}{(r^{2}+l^{2})} \right ] \qquad(2)$

The net electric field at point $P$ due to an electric dipole

$E=E_{+q}\:cos\theta + E_{-q}\: cos\theta \qquad(3)$

Put the value of $E_{+q}$ and $E_{-q}$ in the above equation $(3)$, So equation $(3)$ can also be written as follows

$E=2\left [ \frac{q}{4\pi\epsilon_{0} }\frac{1}{(r^{2}+l^{2})} \right ]cos\theta \qquad (4)$

From figure, In $\Delta \: POB$,

$cos\:\theta=\frac{l}{\sqrt{(r^{2}+l^{2})}}$

Put the value of $cos\theta$ in equation $(4)$, so equation $(4)$ can also be written as follows

$E=\frac{1}{4\pi\epsilon_{0}}\left [ \frac{q\times2l}{(r^{2}+l^{2})^{3/2}} \right ] \qquad (5)$

Here $l \lt r$ so $l^{2} \lt \lt r^{2}$ so neglect the term $l^{2}$ in above equation $(5)$ so we can write above equation

$ E=\frac{1}{4\pi\epsilon_{0}}\left [ \frac{q\times2l}{r^{3}} \right ] \qquad (6)$

$E=\frac{1}{4\pi\epsilon_{0}} \frac{p}{r^{3}} \qquad (7)$

This is the equation of electric field intensity at a point on the equatorial line of an electric dipole.

The vector form of the above equation $(7)$ is

$\overrightarrow{E}=\frac{1}{4\pi\epsilon_{0}} \frac{\overrightarrow{p}}{r^{3}}$

3. Electric field intensity at any point of an electric dipole:

Let us consider, An electric dipole $AB$ of length $2l$ consisting of the charge $+q$ and $-q$. Let's take a point $P$ in general and its position vector is $\overrightarrow{r}$ from the center point $O$ of the electric dipole AB.

Electric field intensity at any point of an electric dipole

The electric dipole moment is a vector quantity that has a direction from $-q$ charge to $+q$ charge. So the electric dipole moment's direction is resolved in two-component one is along the vector position $\overrightarrow{r}$ i.e pcosθ and the other is normal to vector position $\overrightarrow{r}$ i.e $psinθ$. So

Electric field intensity due to dipole moment of component $p\:cos\theta$ {Electric field along the Axial Line }

$ \overrightarrow{E_{\parallel }}=\frac{1}{4\pi\epsilon_{0}} \frac{2pcos\theta}{r^{3}} \qquad(1)$

Electric field intensity due to dipole moment of component $p\:sin\theta$ {Electric field along the Equatorial Line}

$ \overrightarrow{E_{\perp}}=\frac{1}{4\pi\epsilon_{0}} \frac{psin\theta}{r^{3}} \qquad(2)$

The resultant electric field vector $E$ at point $P$

$ \overrightarrow{E}=\sqrt{E_{\perp}^{2}+E_{\parallel}^{2}+2 E_{\perp}E_{\parallel}cos90^{\circ}}$

From figure, The angle between $E_{\perp}$ and $E_{\parallel}$ is $90^{\circ}$. So

$\overrightarrow{E}=\sqrt{E_{\perp}^{2}+E_{\parallel}^{2} }\qquad (3)$

Now substitute the value of equation $(1)$ and equation $(2)$ in equation $(3)$. Then

$ \overrightarrow{E}=\frac{1}{4\pi\epsilon_{0}}\frac{p}{r^{3}}\sqrt{(sin^{2}\theta+4cos^{2}\theta)}$

$ \overrightarrow{E}=\frac{1}{4\pi\epsilon_{0}}\frac{p}{r^{3}}\sqrt{(1+3cos^{2}\theta)}$

This is the equation of electric field intensity at any point due to an electric dipole.

The direction of the resultant electric field intensity vector $\overrightarrow{E}$ from the axial line is

$tan\alpha =\frac{\overrightarrow{E}_{\perp }}{\overrightarrow{E_{\parallel }}} \qquad(4)$

Put the value of $\overrightarrow{E_{\perp}}$ and $\overrightarrow{E_{\parallel}}$ in equation (4). we get

$tan\alpha =\frac{sin\theta}{2cos\theta}$

$tan\alpha =\frac{1}{2}tan\theta$

Here $\alpha$ is the angle between the resultant electric field intensity $\overrightarrow{E}$ and the axial line.

Read More

Definition and Expression of escape velocity of an object on the planet

Definition of Escape Velocity:

The minimum velocity, by which an object is thrown vertically in an upward direction and that object goes out from the gravitation field of the planet and does not come back, is called the escape velocity.

Deduction Escape Velocity Expression:

Let us consider the following:

The mass of the planet =$M$
The radius of the planet = $R$
The mass of the object = $m$

The gravitational force on an object at position $P$ which is a distance $x$ from the surface of the planet

$F=G\frac{M m}{x^{2}} \qquad(1)$

The work done by the force to move the object a very small distance $dx$ from position $A$ to $B$

$W=F.dx$

$dw=G\frac{M m}{x^{2}}dx$

The total work done to move the object from the surface of the planet to infinity

$\int^{W}_{0}dw= \int^{\infty}_{R}G\frac{M m}{x^{2}}dx$

$\left[ w \right]^{W}_{0}=G M m \int^{\infty}_{R} \frac{dx}{x^{2}}$

On solving the above equation

$W=GM m \int^{\infty}_{R} \frac{dx}{x^{2}}$

$W=GM m \left[ -\frac{1}{x} \right]^{\infty}_{R}$

$W=GM m \left[ -\frac{1}{\infty} + \frac{1}{R} \right]$

$W=GM m \left[\frac{1}{R} \right]$

$W=\frac{G M m}{R}$

The above work done is given to the object in the form of kinetic energy to projectile from the surface of the planet to infinity. i.e.

$\frac{1}{2} m v^{2}_{e}= \frac{G M m}{R} $

Where $v_{e}$ is the escape velocity of the object.

$v^{2}_{e} = \frac{2G M m}{R}$

$v_{e} = \sqrt{\frac{2G M}{R}} \qquad(2)$

$v_{e} = \sqrt{\frac{2gR^{2}}{R}} \qquad \left(\because GM=gR^{2} \right)$

$v_{e} = \sqrt{2gR} \qquad(3)$

For earth put mass of the planet $M=M_{e}$ and $R=R_{e}$ in the above equation$(2)$ and equation$(3)$ and we get

$v_{e} = \sqrt{\frac{2G M_{e}}{R_{e}}} $

$v_{e} = \sqrt{2gR_{e}} $

Now substitute the value of the $g=9.8 m/s^{2}$ and radius of earth $R_{e}= 6.4 \times 10^{6} m$ then the escape velocity of the object

$v_{e}=11.2 m/s$

This is the escape velocity of the earth.

Now put $M=\frac{4}{3} \pi R^{3}$ in the above equation $(2)$ then we get

$v_{e} = \sqrt{\frac{2G \frac{4}{3} \pi R^{3}}{R}} $

$v_{e} = \sqrt{\frac{8 \pi \rho G R^{2}}{3}} \qquad(4)$

From the equation $(2)$, $(3)$, and $(4)$ we can conclude that

1.) The escape velocity of the object does not depend on the mass of the object.

2.) The escape velocity of the object is depend upon the mass and radius of the planet.

3.) If the velocity of the object is less than the escape velocity, then the object will reach a certain height and may either move in an orbit around the earth or may fall back to the planet.

4.) If the velocity of projection $(v)$ of the body from the surface of a planet is greater than the escape velocity $v_{e}$ of the planet, the body will escape out from the gravitational field of that planet and will move the interstellar space with velocity $v'$ which can be obtained by using the conservation of energy.

$\frac{1}{2}mv^{2}+\left( -\frac{GMm}{R} \right)= \frac{1}{2}mv'^{2}+0$

$\frac{1}{2}mv^{2}+\left( -\frac{GMm}{R} \right)= \frac{1}{2}mv'^{2}$

$v'^{2}= v^{2} - \frac{2GM}{R}$

$v'^{2}= v^{2} - v^{2}_{e} \qquad \left( \because v^{2}_{e} = \frac{2GM}{R} \right)$

$v'= \sqrt{v^{2} - v^{2}_{e}}$

The relation between orbital velocity and escape velocity of an object:

We know that the orbital velocity of any object revolving near the planet is

$v_{\circ} = \sqrt{gR} \qquad(1)$

The escape velocity of an object which is placed on the planet is

$v_{e} = \sqrt{2gR} \qquad(2)$

From the above equation $(1)$ and equation $(2)$, we get

$v_{e} = \sqrt{2} v_{\circ}$

Alternative Method to Derive Expression for Escape Velocity:

The potential energy of an object on the surface of the planet

$U=-\frac{GMm}{R}$

If the object is thrown vertically in the upward direction with escape velocity $v_{e}$, then the kinetic energy of the object:

$K=\frac{1}{2}mv_{e}^{2}$

We know that the total energy of the object is zero at infinity and then

$K+U=0$

Now substitute the value of $K$ and $U$ in the above equation

$\left( \frac{1}{2}mv_{e}^{2} \right)+\left( -\frac{GMm}{R} \right)=0$

$ \frac{1}{2}mv_{e}^{2} -\frac{GMm}{R} =0$

$ \frac{1}{2}mv_{e}^{2} = \frac{GMm}{R} $

$ \frac{1}{2}v_{e}^{2} = \frac{GM}{R} $

$v_{e}^{2} = \frac{2GM}{R} $

$v_{e} = \sqrt {\frac{2GM}{R}} $

$v_{e} = \sqrt{\frac{2gR^{2}}{R}} \qquad \left(\because GM=gR^{2} \right)$

$v_{e} = \sqrt{2gR} $

Read More

Numerical Problems and Solutions of Centripetal Force and Centripetal Acceleration

Solutions to Numerical Problems of the Centripetal Force and Centripetal Acceleration

Numerical Problems and Solutions

Q.1 An object of mass $0.20 \: Kg$ is being revolved in a circular path of diameter $2.0 \: m$ on a frictionless horizontal plane by means of a string. It performs $10$ revolutions in $3.14 \: s$. Find the centripetal force acting on an object.

Solution:
Given that:
Mass of body $(m)=0.20 \: Kg$
Diameter of Circular path $(d)=2.0: m$
Number of revolutions $(n)=10$
Time taken to complete $(10)$ revolution$(t)=3.14 s$
The centripetal force acting on a body $(F)=?$
Now the centripetal force:
$F=m r \omega^2$
$F=m r \left( \frac{2 \pi n}{t} \right)^2$
Now Substitute the given values in the centripetal force formula:
$F=0.20 \times 1 \left( \frac{2 \times 3.14 \times 10}{3.14} \right)^2$
$F=0.8 N$

Q.2 A car of mass $1200 Kg$ is moving with a speed of $10.5 ms^{-1}$ on a circular path of radius $20 m$ on a level road. What will be the frictional force between the car and the road so that the car does not slip?

Solution:
Given that:
Mass of car $(m) = 1200 \: Kg$
Speed of car $(v) = 10.5: ms^{-1}$
The radius of circular path $(r)= 20 m$
The frictional force $(F)=?$
The frictional force $(F)$ should be equal to the required centripetal force i.e
$F=\frac{mv^{2}}{r}$
Now Substitute the given values in the centripetal force formula:
$F=\frac{1200 \times (10.5)^{2}}{20}$
$F=6.615 \times 10^{3} N$

Q.3 A string can bear a maximum tension of $50 N$ without breaking. A body of mass $1 kg$ is tied to one end of $2 m$ long piece of the string and rotated in a horizontal plane. Find the maximum linear velocity with which the string would not break.

Solution:
Given that:
Maximum tension on the string without breaking $(F)=50 N$
mass of the a body $(m)=1 Kg$
length of the string $(l)=2 m$
The maximum velocity with which the string would not break $(v)=?$
We know that the centripetal force:
$F=\frac{mv^{2}}{r}$
$v=\sqrt{\frac{F \: r}{m}}$
Now Substitute the given values in the centripetal force formula:
$v=\sqrt{\frac{50 \times 2 2}{1}}$
$v=10 ms^{-1}$

Q.4 The moon revolves around the earth in $2.36 \times 10^{6} s$ in a circular orbit of radius $3.85 \times 10^{5} Km$. Calculate the centripetal acceleration produced in the motion of the moon.

Solution:
Given that:
The radius of circular orbit of the moon $(r)=3.85 \times 10^{5} Km = 3.85 \times 10^{8} m$
Time taken to complete one revolution $(T)=2.36 \times 10^{6} s$
Centripetal acceleration produced in the motion of the moon $=?$
The centripetal acceleration:
$a= \omega^{2} r $
$a= \left( \frac{2 pi}{T} \right) r \qquad \left( \because \omega= \frac{2 pi}{T} \right) $
Now Substitute the given values in the centripetal acceleration formula:
$a= \left( \frac{2 \times 3.14}{2.36 \times 10^{6}} \right) \times 3.85 \times 10^{8} $
$a=2.73 \times 10^{-3} ms^{-2} N$

Q.5 Calculate the centripetal acceleration at a point on the equator of the earth. The radius of the earth is $6.4 \times 10^{6} m$ and it completes one rotation per day about its axis.

Solution:
Given that:
Radius of earth $(r)=6.4 \times 10 ^{6} m$
Time taken to complete one rotation per day about its axis$(T)=24 \times 60 \times 60 s$
centripetal acceleration at a point on equator $=?$
The centripetal acceleration:
$a= \omega^{2} r $
$a= \left( \frac{2 pi}{T} \right) r \qquad \left( \because \omega= \frac{2 pi}{T} \right) $
Now Substitute the given values in the centripetal acceleration formula:
$a= \left( \frac{2 \times 3.14}{24 \times 60 \times 60} \right) \times 6.4 \times 10^{6} $
$a=3.37 \times 10^{-2} ms^{-2} N$

Read More

Variation of Acceleration Due to Gravity

Variation in Gravitational Acceleration:

The value of $g$ varies above and below the surface of the earth. It also changes with the latitude at different places and due to the rotation of the earth about its axis. The earth is not a perfect sphere but is approximately an ellipsoid. The radius of the earth is more at the equator and lesser at the poles. The acceleration due to gravity also changes due to the shape of the earth.

1.) Effect of Altitude on Acceleration due to Gravity
2.) Effect of depth below the earth's surface on Acceleration due to Gravity
3.) Effect of the shape of the earth 4.) Effect of rotation about its own axis

1.) Effect of Altitude on Acceleration due to Gravity:

Let us consider: The mass of the earth = $M_{e}$
The radius of the earth = $R_{e}$
A satellite is moving around the earth from the surface of the earth at height= $h$

The gravitational acceleration on the surface of the earth at point $A$

$g=\frac{GM_{e}}{R_{e}^{2}} \qquad (1.1)$

The gravitational acceleration on the altitude $h$ from the surface of the earth at point $B$

$g'=\frac{GM_{e}}{\left( R_{e} + h \right)^{2}} \qquad(1.2)$

Now divide equation $(1.2)$ by equation $(1.1)$

$\frac{g'}{g}= \frac{\frac{GM_{e}}{\left( R_{e} + h \right)^{2}}}{\frac{GM_{e}}{R_{e}^{2}}}$

$\frac{g'}{g}= \frac{R_{e}^{2}}{\left( R_{e} + h \right)^{2}}$

$\frac{g'}{g}= \frac{R_{e}^{2}}{R_{e}^{2} \left( 1 + \frac{h}{R_{e}} \right)^{2}}$

$\frac{g'}{g}= \frac{1}{ \left( 1 + \frac{h}{R_{e}} \right)^{2}}$

$\frac{g'}{g}= \left( 1 + \frac{h}{R_{e}} \right)^{-2}$

Now apply the binomial theorem

$\frac{g'}{g}= 1 - \frac{2h}{R_{e}} + \frac{3h^{2}}{R_{e}^{2}}$

Here $h \lt R_{e}$ then $h^{2} \lt \lt R_{e}^{2}$ so neglect the term of higher power of $\frac{3h^{2}}{R_{e}^{2}}$. Therefore we get

$\frac{g'}{g}= 1 - \frac{2h}{R_{e}} $

$g'= \left( 1 - \frac{2h}{R_{e}} \right) g $

From the above equation it is clear that the value $\left( 1 - \frac{2h}{R_{e}} \right) \lt 1$ then

$g' \lt g$

So, the gravitational acceleration $g$ decreases above the earth's surface.

2.) Effect of depth below the earth's surface on Acceleration due to Gravity:

Let us consider:
The mass of the earth = $M_{e}$
The mass of the earth at depth $h$ from the surface of the earth = $M'_{e}$
The radius of the earth = $R_{e}$

The gravitational acceleration on the surface of the earth at point $A$

$g=\frac{GM_{e}}{R_{e}^{2}} \qquad (2.1)$

The gravitational acceleration at point $B$ on the depth $h$ from the surface of the earth

$g'=\frac{GM'_{e}}{\left( R_{e} - h \right)^{2}} \qquad(2.2)$

Now divide equation $(2.2)$ by equation $(2.1)$

$\frac{g'}{g}= \frac{\frac{GM'_{e}}{\left( R_{e} - h \right)^{2}}}{\frac{GM_{e}}{R_{e}^{2}}}$

$\frac{g'}{g}= \frac{R_{e}^{2}}{\left( R_{e} - h \right)^{2}} \left( \frac{M'_{e}}{M_{e}} \right) \qquad(2.3)$

If $\rho$ is the density of the earth the total mass of the earth and the mass of the earth at depth $h$

$M_{e}=\frac{4}{3}\pi R_{e}^{3} \rho$

$M'_{e}=\frac{4}{3}\pi \left ( R_{e}-h\right)^{3} \rho$

Now subtitute the value of $M_{e}$ and $M'_{e}$ in equaion $(2.3)$

$\frac{g'}{g}= \frac{R_{e}^{2}}{\left( R_{e} - h \right)^{2}} \left( \frac{\frac{4}{3}\pi \left ( R_{e}-h\right)^{3} \rho}{\frac{4}{3}\pi R_{e}^{3} \rho} \right) $

$\frac{g'}{g}= \frac{\left( R_{e} - h \right)}{R_{e}}$

$\frac{g'}{g}= \left( 1 - \frac{h}{R_{e}} \right)$

$g'= \left( 1 - \frac{h}{R_{e}} \right)g$

From the above equation it is clear that the value $\left( 1 - \frac{h}{R_{e}} \right) \lt 1$ then

$g' \lt g$

So, the gravitational acceleration $g$ decreases below the earth's surface.

3.) Effect of the shape of the earth:

Earth is not a perfect sphere. It is flattened at the poles and bulges out at the equator. The equatorial radius $R_{E}$ of the earth is about $21 Km$ Then greater than the polar radius $R_{P}$. Now from the equation $g=\frac{GM}{R^{2}}$ $\left (i.e. g \propto \frac{1}{R^{2}} \right)$, we can conclude that the higher radius has less gravitational acceleration because of that the value of $g$ is least at equator and maximum at the pole.

4.) Effect of rotation about its own axis:

Latitude at a plane is defined as the angle at which the line joining the place to the centre of the earth, makes with the equatorial plane. It is generally denoted by the $\lambda$.

From the figure given below, the latitude at a place $P = \angle OPC = \lambda$

Consider earth is in a perfect sphere of mass $M_{e}$, radius $R_{e}$ with centre $O$. The whole mass of the earth is supposed to be concentrated at the centre $O$. As the earth rotates about its polar axis from west to east, every particle lying on its surface moves along a horizontal circle with the same angular velocity as that of the earth. The centre of each circle lies on the polar axis.

Let us consider, a particle of mass $m$ at a place $P$ of latitude $\lambda$. If the earth is rotating about its polar axis $NS$ with constant angular velocity $\omega$, then the particle also rotates and describes a horizontal circle of radius $r$, Where

$r=PC=OP \: cos\lambda = R \: cos\lambda \qquad (3.1)$

The centrifugal force acting on the particle at $P$ is $m\: r \: \omega^{2}$. It acts along $PA$ directed away from the centre $C$ of the circle of rotation.

The true weight of the particle = $mg$

The centrifugal force at P = $m\: r \: \omega^{2}$

So the resultant of true weight and centrifugal force is $mg'$ can be found by Using the parallelogram law of the forces i.e

$mg'=\sqrt{(mg)^{2}+(mr\omega^{2})^{2}+2(mg)(mr\omega^{2})cos (180^{\circ}- \lambda)}$

$g'=\sqrt{(g)^{2}+(r\omega^{2})^{2}+2(g)(r\omega^{2})cos\lambda)}$

$g'=\sqrt{(g)^{2}+(\omega^{2} R \: cos \lambda )^{2}+2(g)( \omega^{2} R \: cos \lambda )cos\lambda)} \qquad \left( \because r=R \: cos \lambda \right)$

$g'=g \left( 1 + \frac{R^{2}\omega^{4}}{g^{2}} cos^{2} \lambda - \frac{2R \omega^{2}}{g} cos^{2} \lambda)\right)^{\frac{1}{2}}$

Here the value of $\frac{R \omega^{2}}{g}$ is very small, therefore the terms with its squares and of higher power can be neglected. So the above equation can be written as:

$g'=g \left( 1 - \frac{2R \omega^{2}}{g} cos^{2} \lambda)\right)^{\frac{1}{2}}$

Now apply the binomial theorem, and we get

$g'=g \left( 1 - \frac{1}{2}\frac{2R \omega^{2}}{g} cos^{2} \lambda)\right)$

$g'=g \left( 1 - \frac{R \omega^{2}}{g} cos^{2} \lambda)\right)$

$g'= \left( g - R \omega^{2} cos^{2} \lambda\right) \qquad(3.2)$

As, $cos \lambda$ and $\omega$ are positive, therefore $g' \lt g$. Thus from the above equation, it is clear that acceleration due to gravity:

i.) Decreases on account of the rotation of the earth
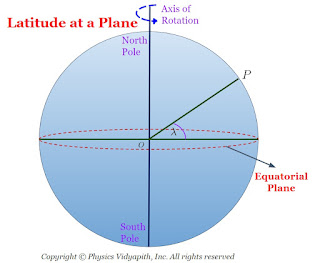
ii.) Increases with the increase in the latitude of the place.

At equator,
$\lambda = 0^{\circ}$
$g'=p_{e}$
Then from above equation $(3.2)$,

$g_{e}=g-R\omega^{2}$

Clearly, $g_{e}$ is minimum.

At pole,
$\lambda = 90^{\circ}$
$g'=g_{p}$
Then from above equation $(3.2)$,

$g_{p}=g-R\omega^{2 (0)}$

$g_{P}=g$

Clearly, $g_{p}$ is maximum.

Hence, the value of acceleration due to gravity is minimum at the equator and maximum at the poles. The value of acceleration due to gravity at the poles will remain unchanged whether the earth is at rest or rotating.

The difference in the value of acceleration due to gravity at the pole and equator:

We know that:

Acceleration due to gravity at the equator is

$g_{e}=g-R\omega^{2}$

Acceleration due to gravity at the pole is

$g_{p}=g$

The difference in gravitational acceleration at the equator and pole

$g_{p} - g_{e}= g - \left(g-R\: \omega^{2} \right)$

$g_{p} - g_{e}= R\: \omega^{2}$

$g_{p} - g_{e}= R\: \left( \frac{2 \pi }{T}\right)^{2}$

Now put $T=24 \times 60 \times 100$

$g_{p} - g_{e} \approx 0.034 m/sec^{2}$

Read More