Difference between Heat and Temperature

Heat :

1. The energy of hotness and coldness of the body is called the heat

2. Heat is the total kinetic energy of all the particles in a body, i.e., it is the sum of the kinetic energies of each individual particle in the body.

3. Heat is that form of energy which flows from a hot body to a cold body when they are kept in contact.

4. The amount of heat inside the body depends on mass, temperature, and the nature of the body.

5. The body's heat is measured by the principle of calorimetry.

6. Two bodies with the same amount of heat may differ in temperature.

7. When two bodies are placed in contact, the total amount of heat is equal to the sum of the heat of the individual bodies.

8. The heat can only be a positive value.

9. The S.I. unit of heat is $joule (J)$.

Temperature:

1. The measurement of energy (i.e., average energy) of hotness and coldness of the body is called temperature.

2. The body's temperature is equal to the average kinetic energy of all the particles in the body.

3. Temperature is a parameter that determines the direction of the flow of heat while keeping the two bodies at different temperatures in contact.

4. The temperature of a body depends on the average motion of the particles.

5. The thermometer is used to measure the body's temperature.

6. Two bodies at the same temperature may differ in the quantities of heat contained in them.

7. When two bodies having different temperatures are placed in contact, then the resultant temperature is a temperature between the two temperatures.

8. The temperature can be positive or negative value both.

8. The S.I. unit of temperature is $kelvin (K)$.

Read More

Difference between Heat Capacity and Specific Heat Capacity

Heat capacity:

1. Heat capacity is the amount of heat energy required to raise the temperature of the entire body by $1^{\circ}C$.

2. Heat capacity depends on both the nature of the substance and the mass of the body. As the mass of the body increases, the heat capacity of the body also increases.

3. Heat capacity

$C=\frac{Q}{\Delta t}\\ C = mass (m) \times specific \: heat \: capacity (c)$

4. The heat capacity's unit is $J-K^{-1}$.

Specific heat capacity:

1. Specific heat capacity is the amount of heat energy required to raise the temperature of the unit mass of the body by $1^{\circ}C$.

2. Specific heat capacity does not depend on the mass of the body, but it is a characteristic property of the substance of the body.

3. Specific heat capacity

$C=\frac{Q}{m\Delta t} \\ C=\frac{Heat \: Capacity \: (C)}{Mass (m)}$

4. Its unit is $J-kg^{-l}-K^{-1}$.

Read More

Description dielectric materials and their types

Dielectric Materials:

Materials that do not allow current to flow through them are called insulators or dielectrics. Dielectric materials are capable of storing electric energy. Dielectric materials do not have free electrons ( in the case of ideal dielectric) because electrons are tightly bound with the nucleus so the conductivity of the dielectric is poor and for an ideal dielectric, it is zero.

When a dielectric is placed in an external electric field, atoms or molecules of the dielectric material are polarised due to the creation of an electric dipole in the atoms or molecules, and the internal field is set up in the dielectric material which opposes the external applied electric field, thereby reducing the net electric field and hence the electric potential difference. If these dielectrics are placed between plates of a capacitor, the potential difference will be reduced without affecting the charge on the plates.

According to the band theory of solids,

A dielectric is a material in which the energy band gap between balance and conduction band is more than three electron volt.

Examples: Glass, Plastic, Mica, Rubber, Wood, Turpentine oil etc.

Types of Dielectric materials:

Dielectric materials are of two types :

1.) Non-polar dielectrics
2.) Polar dielectric

1.) Non-polar dielectrics:

In non-polar dielectric materials, the molecules that are usually diatomic and composed of the same type of two atoms have a symmetrical structure that is the positive nuclei are surrounded by a symmetrically distributed negative electron cloud. The center of gravity of positive and negative charge distribution coincide and so the molecules are electrically neutral and have zero electric dipole moment.

Examples: $H_{2}$, $O_{2}$, $CO_{2}$, $CCl_{4}$, $C_{6}H_{6}$, $C_{6}H_{12}$, $CS_{2}$ etc.

Polarisation of the non-polar dielectric materials:

When a non-polar dielectric is placed in an external electric field the positive charge of the nucleus and negative charge of the electron cloud experience electric force which causes a displacement between the positive and negative parts of the molecule from their equilibrium position in opposite directions. The distance moved is very small $(10^{-10})$ because the displacement is restricted by storing force which increases with the increase of displacement. Therefore the centre of gravity of these positive and negative charges no longer coincide and molecules are said to be polarized. The molecules does acquire an induced electric dipole moment and aligned in the direction of external field. The induced dipole moment and the polarization disappear when an electric field is removed.

2.) Polar Dielectrics:

In polar dielectric materials, the molecules which are normally composed of two or more different atoms have permanent dipole moments because the center of gravity of these positive charges and that of the negative charges in a molecule are permanently separated by a finite but small distance. This is due to the asymmetric shape of the molecule. Thus each molecule in the polar dielectric material behaves as a dipole having a permanent dipole moment. Normally these molecules are in polar dielectrics and randomly arranged such that the net dipole moment is zero and the material acts as a neutral one.

Examples: $H_{2}O$, $CHCl_{3}$, $C_{6}H_{5}Cl$, $C_{6}H_{5}NO_{2}$, $C_{2}H_{5}OH$, $NH_{3}$, $HCl$, $CO$,etc.

Polarization of the polar dielectric materials:

when polar dielectric is placed in an external electric field the molecular dipole tense to align themselves in the direction of the field and acquire a considerable amount of dipole moment. this the dielectric acid to be polarised.

In the $HCL$ molecule, the electron of the $H$ atom lies more toward the $Cl$ atom. The $H$ end of the $HCl$ molecule is positive and the $Cl$ end is negative. The molecule is therefore a dipole having dipole moment $\overrightarrow{p}$ direct from $Cl$ atom to $H$ atom.

Hence, the polarization of non-polar dielectric material is the displacement of positive and negative charge, and in the case of polar dielectric material, the polarization is the orientation of molecular dipole moment under the action of the electric field to which they are subject.

Read More

Difference between Potentiometer and Voltmeter

There are the following differences between a potentiometer and a voltmeter given below:

Potentiometer:

1.) It is based on null method.

2.) It gives an accurate value of emf.

3.) While measuring emf, it does not draw any current from the cell.

4.) Resistance of potentiometer wire becomes infinite while measuring emf.

5.) It can be used for various experimental purposes.

6.) It can not be taken conveniently from one place to another place.

Voltmeter:

1.) It is based on the deflection method.

2.) It does not give an accurate value of emf.

3.) While measuring emf, it draws some current from the cell. Hence it reads slightly less than the actual emf.

4.) The resistance of the voltmeter is high enough but not infinite.

5.) It can be used to measure potential differences only.

6.) It can be conveniently taken from one place to another place.

Read More

Principle Construction, Working and Angular Magnification of Simple Microscope

Principle of Simple Microscope:

The principle of the simple microscope is based on the magnification of an image by using a simple convex lens.

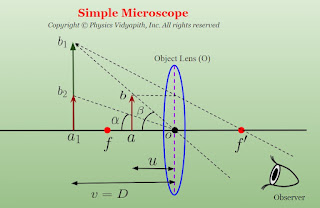
Construction:

A simple microscope consists of one convergent lens only. The object is placed between the lens and its focal length, and the eye is placed just behind the lens. Then the eye sees a magnified, erect, and virtual image on the same side as the object at the least distance of distinct vision $(D)$ from the eye, and the image is then seen most distinctly.

Working:

If the small object $ab$ is placed between a lens $O$ and its first focus $f$ then Its magnified virtual image $a_{1}b_{1}$ is formed at a distance $D$ from the lens. Since the eye is just behind the lens, the distance of image $a_{1}b_{1}$ from the eye is also $D$.

Angular Magnification Or Magnifying Power($M$):

The ratio of the angle subtended by the image at the eye ($\beta$) to the angle subtended by the object at the eye when placed at the least distance of distinct vision ($\alpha$) is called the angular magnification or magnifying power.

$M= \frac{Angle \: subtended \: by \: the \: image \: at \: the \: eye \: (\beta)}{Angle \: subtended \: by \: the \: object \: at \: the \: eye \: when \\ placed \: at \: least \: distance \: of \: distinct \: vision \: (\alpha)}$

$M=\frac{\beta}{\alpha} \approx \frac{tan \beta}{tan \alpha} \quad (1)$

From figure

$tan \beta = \frac{ab}{oa} $

$tan \alpha = \frac{a_{1}b_{2}}{a_{1}o}$

Here $a_{1}b_{2} = ab$

$tan \alpha = \frac{ab}{a_{1}o}$

Now substitute these values in equation $(1)$, then

$M=\frac{\frac{ab}{ao}}{\frac{ab}{a_{1}o}}$

$M=\frac{a_{1}o}{ao}$

Here $ao = u$ (Distance between object and optical center of the lens) and $a_{1}o = D$ (Least Distance of distinct vision), then the above equation can be written as

$M=\frac{D}{u} \qquad(2)$

We know that the lens formula $\frac{1}{v}-\frac{1}{u} = \frac{1}{f}$

Now put
$v=-D$ (The image $a'b'$ is being formed at a distance $D$ from lens)
$u=-u$

$\frac{1}{-D}-\frac{1}{-u} = \frac{1}{f}$

Multiply $D$ in the above equation

$-\frac{D}{D}-\frac{D}{-u} = \frac{D}{f}$

$-1-\frac{D}{-u} = \frac{D}{f}$

$\frac{D}{u} =1 + \frac{D}{f} \qquad(3)$

From equation $(2)$ and equation $(3)$, then

$M=1 + \frac{D}{f} $

If eye is kept at distance $d$ from lens then $v=-(D-d)$, and the magnifying power will be

$M=1+\frac{D-d}{f}$

To see with a relaxed eye, the image $a'b'$ should be formed at infinity. In this case, the object $ab$ will be at the focus of the lens, i.e. $u=f$ then magnifying power

$M= \frac{D}{f} $

Read More