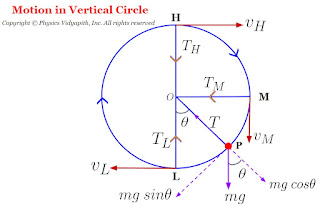
Calculation of Motion of a body in a vertical Circle: Let us consider, A body that has mass $m$ moving in a vertical circle of radius $r$. If at any instant the body is at position $P$ with angular displacement $\theta$ from the lower position $L$ of the circle. As shown in the figure below.
The various forces acting on the body are:
The weight $mg$ of the body, acting vertically downwards
Tension $T$in the string acting along the $PO$. Now $mg$ can be resolved into two components:
1.) The horizontal component $mg cos\theta$ opposite to $T$
2.) The vertical component $mg sin\theta$ act along tangent to the circle at $P$
So the net force on the body at position $P$ provides the necessary centripetal force required by the body
$T-mg cos\theta = \frac{m v^{2}}{r}$
$T= \frac{m v^{2}}{r} + mg \: cos\theta \qquad(1)$
Tension and velocity at the highest position $H$ of the verticle circle: At the highest position $H$ the tension $T_{H}$ of the will be minimum and the velocity $v_{H}$ will also be minimum.
If $cos\theta = -1$ i.e. $\theta=180^{\circ}$
Then Tension $T$ and velocity $v$ will be minimum i.e $T_{H}$ and $v_{H}$
so from equation $(1)$
$T_{H}= \frac{m v_{H}^{2}}{r} - mg $
So from the above equation, we can conclude that The body will move along the vertical circle only when $T_{H} \geq 0$
$\left( \frac{m v_{H}^{2}}{r} - mg \right) \geq 0$
$ \frac{m v_{H}^{2}}{r} \geq mg $
$ \frac{ v_{H}^{2}}{r} \geq g $
$ v_{H} \geq \sqrt {rg} $
Thus the minimum value of the velocity at the highest position is $\sqrt{rg}$
Tension and velocity at lowest position $L$ of the verticle circle: At the lowest position $L$ the tension and velocity will be maximum. Now applying the principle of energy conservation for the position $H$ and $L$ of the body.
Total energy at $L$ =Total energy at $H$
$\frac{1}{2}m v_{L}^{2}=\frac{1}{2}m v_{H}^{2} +mg(2r)$
Now substitute the value of $v_{H} \geq \sqrt{gr}$ in above equation then we get
$\frac{1}{2}m v_{L}^{2}=\frac{1}{2}m (gr) +mg(2r)$
$\frac{1}{2}m v_{L}^{2}=\frac{5mgr}{2}$
$v_{L} \geq \sqrt{5gr}$
For the maximum value of tension $T_{L}$ at the lowest position $L$ of the vertical circle. Now put $cos \theta =1$ i.e $\theta=0^{\circ}$ in the equation $(1)$ then we get
$T_{L}= \frac{m v_{L}^{2}}{r} + mg $
Now substitute the value of $v_{L} \geq \sqrt{5gr}$ in the above equation then
$T_{L} \geq \frac{m 5gr}{r} + mg $
$T_{L} \geq 6gr$
Tension and velocity at horizontal position $M$ of the verticle circle:
Now apply the principle of conservation of energy for position $M$ and position $L$
Total energy at $M$ =Total energy at $L$
$ \frac{1}{2}m v_{M}^{2} + mgr = \frac{1}{2} m v_{L}^{2}$
$ \frac{1}{2}m v_{M}^{2} = \frac{1}{2} m v_{L}^{2} - mgr$
Now substitute the value of $v_{L} \geq \sqrt{5gr}$ in the above equation then
$ \frac{1}{2}m v_{M}^{2} \geq \frac{1}{2} m 5gr - mgr$
$ \frac{1}{2}m v_{M}^{2} \geq \frac{3 mgr}{2}$
$v_{M}^{2} \geq 3 gr$
$v_{M} \geq \sqrt{3 gr}$
To find the tension $T_{M}$ at position $M$ substitute the $cos \theta =0$ i.e $\theta =90^{\circ}$ in equation $(1)$. Then we get
$T_{M} = \frac{m v_{M}^{2}}{r} + 0$
$T_{M} = \frac{m v_{M}^{2}}{r}$
Now substitute the value of $v_{M} \geq \sqrt{3gr}$ in the above equation. Then we get
$T_{M} \geq 3mg$
Practical Application of motion in a vertical Circle:
1.) When a bucket containing water is rotated in a vertical circle with a velocity at the lowest point $v_{L} \geq \sqrt{5gr}$, water shall not spill even at the highest point, when the bucket is upside down. If the bucket is whirled slowly, so that $ \left(mg \gt \frac{mv_{H}^{2}}{r} \right) $, then a part of the weight shall provide the necessary centripetal force $\left( \frac{mv_{H}^{2}}{r} \right)$; and the rest of the weight of water $\left( mg - \frac{mv_{H}^{2}}{r} \right) $ causes some water to accelerate downwards and spill. Only this much water shall leave the bucket.
2.) A pilot of an aircraft can successfully loop a vertical loop without falling at the top of the loop (being without a belt) when its velocity at the bottom of the loop is $\geq \sqrt{5gr}$
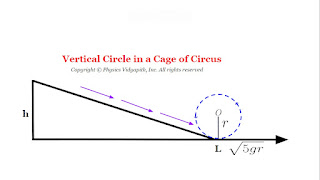
3.) In a circus, a motorcyclist is able to perform the feat of driving the motorcycle along a vertical circle in a cage. The motorcyclist does not fall even at the highest point, when his velocity at the bottom of the cage is $\geq \sqrt{5gr}$.
To acquire this velocity at the lowest point $L$ of the vertical circle of radius $r$, he has to roll down a vertical height $h$, As shown in the figure below:
From the equation of motion $v^{2}=u^{2}+2as$
Let $u=0$, $a=+g$ and $s=h$
we get, $v^{2}=0 +2gh$
$v=\sqrt{2gh}$
To move in a vertical circle, the velocity $v$ acquired at $L$ must at least be equal to $\sqrt{5gr}$. i.e.
$\sqrt{2gh}= \sqrt{5gr}$
$h=\frac{5r}{2}$
Definition of work done and its essential condition
Work: When a force is applied on a body and a body is displaced along the line of action of force then this is called the work done by force. Work is a scalar quantity.
Unit: $Joule$, $N-m$
Dimension: $[ML^{2}T^{-2}]$
Example: When a boy kicks a football to move it, the boy is said to have done some work.
Let us consider, A body that has mass $m$. If a force $F$ applied on a body at an angle $\theta$ and body is displaced from position $A$ to position $B$ with distance $d$ then work done by force:
$W= horizontal \: component \: of \: the \: force \times displacement $
$W=F\:cos\theta \times d$
$W=F d\:cos\theta \qquad(1)$
$W=\overrightarrow{F}. \overrightarrow{d}$
So, we can conclude from the above equation that "The work done by the force is the scalar product of the force and displacement ".
Note: When the force is applied at an angle $\theta$ then the vertical component of the force is balanced by weight $mg$ and the horizontal component of the force is responsible for the motion of the body.
Essential Condition for work to be done:
For work to be done, the following two conditions should be satisfied
A force should act on the body.
The body should move in the direction of the force, or opposite to it, i.e the point of application of the force should move in the direction of the force or opposite to it. In other words, the body must be displaced
Types of Work done by force:
Positive Work done
Zero Work done
Negative Work done
Positive Work done: When a force is applied on a body and the body is displaced along in direction of the force then this is called the positive work done by force.
If $\theta=0 ^{\circ}$, then $cos0 ^{\circ} =1$
the from equation $(1)$
So Work done by force
$W=Fd$
Zero Work done: When a force is applied on a body and the body is not displaced from its position then this is called the zero work done by force.
If $\theta=90 ^{\circ}$, then $cos90 ^{\circ} =0$
then from equation $(1)$
So Work done by force
$W=0$
Negative Work done: When a force is applied on the body and a body is displaced along in the opposite direction of the force then this is called the negative work done by force.
If $\theta=180^{\circ}$, then $cos 0^{\circ} =-1$
then from equation $(1)$
So Work done by force
$W=-Fd$
** 1 Joule Work done: When $1 \: Newton$ of force is applied on a body and a body is displaced by $1\: m$ along the line of action of force then this is called the $1 \: Joule$ work done by force.**
Principle and Proof of Law of Conservation of Energy
Law of Conservation of Energy: According to this principle
Proof of Conservation's Law of Energy: Let us consider, A particle is freely falling from height $h$ under the gravitational acceleration $g$. So the total energy of the particle at different points :
Calculation of Total Energy at Point $A$:
The initial velocity of the particle at point $A$ is $(v_{A})=0$
The kinetic energy of the particle at point $A$ is $(K_{A})=\frac{1}{2}mv_{A}^{2}$
$K_{A}=0\qquad \left( \because v_{A}=0 \right)$
The potential energy of the particle at point $A$ is $(U_{A})=mgh$
The total energy of a particle at point $A$ is $(E_{A})=K_{A}+U_{A}$
Now substitute the value of $K_{A}$ and $U_{A}$ in the above equation. Now the above equation can be written as:
$E_{A}=0+mgh$
$E_{A}=mgh \qquad(1)$
Calculation of Total Energy at Point $B$: If a particle travels the distance $x$ and reaches point $B$ then velocity at point $B$ can be calculated by the equation of motion. i.e.
$v_{B}^{2}=v_{A}^{2}+2gx$
But the initial velocity of the particle is zero. i.e $v_{A}=0$ then the above equation can be written as
$v_{B}^{2}=0+2gx$
$v_{B}^{2}=2gx$
The kinetic energy of the particle at point $B$ is $(K_{B})=\frac{1}{2}mv_{B}^{2}$
Now substitute the value of $v_{B}^{2}$ in the above equation. Now the above equation can be written as:
$K_{B}=\frac{1}{2}m \left( 2g x \right)$
$K_{B}=mgx $
The height of the particle at point $B$ is $(h-x)$ then the potential energy at point $B$ is $(U_{B})=mg(h-x)$
The total energy of a particle at point $B$ is $(E_{B})=K_{B}+U_{B}$
Now substitute the value of $K_{B}$ and $U_{B}$ in the above equation. Now the above equation can be written as:
$E_{B}=mgx+mg(h-x)$
$E_{B}=mgh \qquad(2)$
Calculation of Total Energy at Point $C$: Now the particle reaches point $C$ by traveling distance $h$ from the initial point $A$. This point $C$ is just before the collision from the surface. So the velocity of the particle at point $C$.
$v_{C}^{2}= v_{A}^{2}+2gh$
$v_{C}^{2}= 0+2gh \qquad \left( v_{A}=0 \right)$
$v_{C}^{2}= 2gh$
The kinetic energy of the particle at point $C$ is $(K_{C})=\frac{1}{2}mv_{C}^{2}$
Now substitute the value of $v_{C}^{2}$ in the above equation. Now the above equation can be written as:
$K_{C}=\frac{1}{2}(2mgh)$
$K_{C}=mgh$
At point $C$ the particle is just above the surface so the height $h$ of the object will be zero. i.e. $h=0$
The potential energy at point $C$ is $(U_{C})=0$
The total energy of the particle at point $C$ is $(E_{C})=K_{C}+U_{C}$
Now substitute the value of $K_{C}$ and $U_{C}$ in the above equation. Now the above equation can be written as:
$E_{C}=mgh+0$
$E_{C}=mgh \qquad(3)$
From the above equation $(1)$, equation $(2)$ and equation $(3)$, we get
$E_{A}=E_{B}=E_{C}$
Now we can conclude that the total energy of the particle is always conserved when there is no external influence applied. This is proof of the law of conservation of Energy.
The energy is neither created nor destroyed. The energy can be changed from one form to another form. i.e. when there is not any external influence is applied on the particle then the total energy of the particle is always conserved.
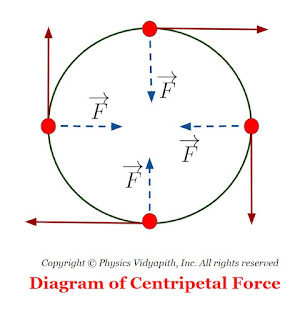
Definition and Practical Applications of Centripetal Force
Definition of Centripetal Force:
This force is also known as a radial force because the direction of force is toward the centre of the circle.
Let us consider, A particle of mass $m$ moving around a circular path of radius $r$ with linear velocity $v$. So the force on a particle:
$F=ma$
Where $a$ is centripetal acceleration i.e. $a=\frac{v^{2}}{r}$. So the force on a particle can be written as
$F=m\frac{v^{2}}{r}$
$F=\frac{mv^{2}}{r}$
$F=m\frac{(r \omega)^{2}}{r} \qquad \left( \because v=r \omega \right)$
$F=mr\omega^{2}$
$F=mr\left(\frac{2\pi}{T}\right)^{2} \qquad \left( \because \omega=\frac{2\pi}{T} \right)$
$F=mr\frac{4\pi^{2}}{T^{2}}$
$F= \frac{4 \pi^{2} m r}{T^{2}} $
$F=4 \pi^{2} m r n^{2} \qquad \left( \because n=\frac{1}{T} \right)$
Practical Applications of Centripetal Force:
1. The planets revolve around the sun and the necessary centripetal force is achieved by gravitational force between the sun and the planet. as shown in the figure below
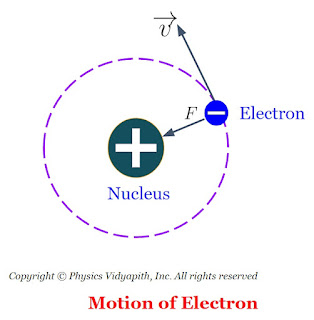
2. The electrons revolve around the nucleus of the atom and the necessary centripetal force is achieved by the force of attraction on the revolving electrons and protons in the nucleus. as shown in the figure below
3. In this case, When a piece of stone is tied to the end of a string whose other end is held in the hand then the required centripetal force, to revolve the stone in a circular path, is achieved by the tension of the string.
4. When a motor car is moving in a curved path then the necessary centripetal force is achieved by friction between the wheels and the road.
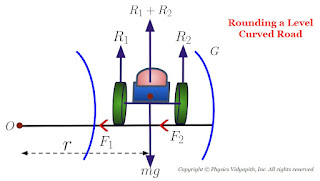
5. Rounding a Level Curve Road:
When a vehicle goes in round a curved road, it requires some centripetal force. While rounding the curve, the wheels of the vehicle have a tendency to leave the curved path and regain the straight line path. The force of friction between the wheels and the road opposes this tendency of the wheels. This frictional force acts towards the centre of the circular track and provides the required centripetal force.
The forces acting on moving vehicles on the curved road are
Weight $mg$ of the vehicle act vertically downward
Normal reaction $R_{1}$ and $R_{2}$ from both sides of the wheels act vertically upward from the horizontal surface
The frictional force $F_{1}$ and $F_{2}$ from both sides of wheels of the vehicle
Hence, the centripetal force is provided by friction force only, therefore
$\frac{mv^{2}}{r} \leq F_{1}+F_{2}$
Where $F_{1}=\mu R_{1}$ and $F_{2}=\mu R_{2}$, then
$\frac{mv^{2}}{r} \leq \mu R_{1}+\mu R_{2}$
$\frac{mv^{2}}{r} \leq \mu \left( R_{1}+ R_{2} \right)$
$\frac{mv^{2}}{r} \leq \mu R \qquad \left( R= R_{1}+ R_{2} \right)$
$\frac{mv^{2}}{r} \leq \mu mg \qquad \left(R=mg \right)$
$\frac{v^{2}}{r} \leq \mu g $
$v^{2} \leq \mu r g$
$v \leq \sqrt{\mu r g}$
Here, $\mu$ is the frictional coefficient.
This is the maximum velocity of the vehicle for rounding on a level curved road without sliding. But the value is very low as it depends on the friction coefficient.
6. Banking of roads: The phenomenon of raising the outer age of the curved road above the inner age is called the banking of roads.
When a vehicle moves on the curved path at a reasonable speed without slipping then sufficient centripetal force is required to move in a curved path which is achieved by banking of the road.
In the case of the Banking of roads, The centripetal force is not provided by friction between the wheels and the road.
Calculation of the angle of banking:
Let us consider, A vehicle of mass $m$ moving around the curved path of radius $r$ with velocity $v$ on a road banking through an angle $\theta$. The forces applying to the vehicle are:
A.) The weight $mg$ act vertically downward.
B.) Normal reaction $R$ of the ground acts perpendicular to the banked road and can be resolved into two components. i.e. Verticle component $R sin\theta$ and Horizontal component $R cos\theta$.
C.) The horizontal component $R cos\theta$ is balanced by the weight $mg$ of the vehicle. i.e.
$R cos\theta= mg \qquad (1)$.
D.) The vertical component of normal reaction $R sin\theta$ acts along the horizontal towards the centre of the circular path and it provides the centripetal force. i.e.
$R sin\theta=\frac{mv^{2}}{r} \qquad (2)$
Now divide equation $(2)$ and equation $(1)$
$\frac{R sin\theta}{R cos\theta}= \frac{\frac{mv^{2}}{r}}{mg}$
$\frac{ sin\theta}{ cos\theta}=\frac{v^{2}}{rg} $
$ tan\theta=\frac{v^{2}}{rg} \qquad(3)$
If $h$ is the height $AB$ of the outer edge of the road above the inner edge and $b$ is the breadth $OB$ of the road then from the figure:
$OA=\sqrt {(OB)^{2}-(AB)^{2}}$
$OA=\sqrt {b^{2}-h^{2}}$
$tan\theta=\frac{AB}{OA}$
$tan\theta=\frac{h}{\sqrt {b^{2}-h^{2}}} \qquad (4)$
From equation $(3)$ and equation $(4)$
$tan\theta=\frac{v^{2}}{rg}=\frac{h}{\sqrt {b^{2}-h^{2}}}$
From the above equation, we can calculate $h$. Usually $h << b$. Therefore, $h^{2}$ is negligibly small compared to $b^{2}$. The above equation can be written as:
$tan\theta=\frac{v^{2}}{rg}=\frac{h}{b}$
Roads are usually banked for the average speed of the vehicle passing over them. However, If the speed of a vehicle is somewhat less or more than this, the self-adjusting static friction will operate between the tyres and the road, and the Vehicle will not skid.
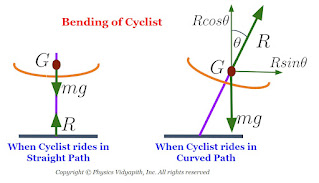
7. Bending of Cyclist: When a cyclist takes a turn on the curved path then the cyclist has to bend the cycle a little inwards from his vertical position to achieve the necessary centripetal force.
Calculation of the angle of bending:
Let us consider, The cyclist of mass $m$ moving around the curved path of radius $r$ with velocity $V$. The force acting on the cyclist:
A.) The weight $mg$ act vertically downward.
B.) Normal reaction $R$ of the ground act on the cyclist at an angle $\theta$ with the verticle and can be resolved into two components. i.e. Verticle component $R sin\theta$ and Horizontal component $R cos\theta$.
C.) The horizontal component $R cos\theta$ is balanced by the weight $mg$ of the cyclist. i.e.
$R cos\theta= mg \qquad (1)$.
D.) The vertical component $R sin\theta$ acts along the horizontal towards the centre of the circular path and it provides the centripetal force. i.e.
$R sin\theta=\frac{mv^{2}}{r} \qquad (2)$
Now divide equation $(2)$ and equation $(1)$
$\frac{R sin\theta}{R cos\theta}= \frac{\frac{mv^{2}}{r}}{mg}$
$\frac{ sin\theta}{ cos\theta}=\frac{v^{2}}{gr}$
$ tan\theta=\frac{v^{2}}{gr}$
$ \theta=tan ^{-1} \left( \frac{v^{2}}{gr} \right)$
When a particle moves in a circular path then a force act, toward the centre of the circle, on a particle. This type of force is called the centripetal force.
| $ \theta=tan ^{-1} \left( \frac{v^{2}}{gr} \right)$ |
Definition and Derivation of Centripetal Acceleration
Definition:
Derivation of Centripetal Acceleration: Let us consider, A particle that has mass $m$ moving with velocity $v$ in a circular path of radius $r$.
If a particle is moving from point $P_{1}$ to point $P_{2}$ by covering distance $\Delta s$ on the circumference of the circle by making an angular displacement of $\theta$ at the center $O$ of the circle.
The direction of velocity of the particle at point $P_{1}$ and $P_{2}$ is $\overrightarrow{v_{1}}$ and $v_{2}$.
Now take the change in velocity from point $P_{1}$ to $P_{2}$ by vector subtraction method as shown in figure below:
To find the expression for the centripetal acceleration, Now take two similar triangles $\Delta OP_{1}P_{2}$ and $\Delta ABC$ from the figure:
$\frac{OP_{1}}{AB}=\frac{P_{1}P_{2}}{BC}$
Now substitute the values from the figure in the above equation i.e.
$\frac{r}{v}=\frac{\Delta s}{\Delta v}$
$\Delta v = \frac{v}{r} \Delta s $
Now divide by $\Delta t$ into both sides the above equation can be written as
$\frac{\Delta v}{\Delta t}=\frac{v}{r} \frac{\Delta s}{\Delta t}$
If $\Delta t$ is tends to zero i.e. $\Delta t \rightarrow 0$ then
$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta v}{\Delta t}=\frac{v}{r} \: \underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta s}{\Delta t}$
Where
$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta v}{\Delta t} \rightarrow$ Instantaneous Acceleration. It is also known as Centripetal Acceleration $(a)$
$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta s}{\Delta t} \rightarrow$ Instantaneous Velocity $(v)$
Now the above equation can be written as
$a = \frac{v^{2}}{r} $
$a = \frac{(r\omega)^{2}}{r} \quad \left( \because v=r\omega \right)$
$a = r \omega ^{2} $
When a particle moves in a circular path then acceleration act on the particle which has a direction toward the center of the circle. This acceleration is called centripetal acceleration.
$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta v}{\Delta t} \rightarrow$ Instantaneous Acceleration. It is also known as Centripetal Acceleration $(a)$
Relation between angular acceleration and linear acceleration
Equation for the relation between linear acceleration and angular acceleration:
Deduce the equation from the General Method:
We know that angular acceleration is
$\alpha=\frac{\Delta \omega}{\Delta t} \qquad (1)$
$\alpha=\frac{\Delta (v/r)}{\Delta t} \qquad \left( \because \omega=\frac{v}{r} \right)$
$\alpha=\frac{1}{r} \frac{\Delta v}{\Delta t}$
If $\Delta t \rightarrow 0$, then the above equation can be written as
$\alpha=\frac{1}{r} \: \underset{\Delta t \rightarrow 0}{Lim} \frac{\Delta v}{\Delta t}$
Where
$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta v}{\Delta t} \rightarrow$ Instantaneous Acceleration $(a)$
$\alpha=\frac{a}{r}$
Deduce the equation from the Differential Method
We know that angular acceleration is
$\alpha=\frac{d \omega}{dt} \qquad (1)$
$\alpha=\frac{d (v/r)}{dt} \qquad \left( \because \omega=\frac{v}{r} \right)$
$\alpha=\frac{1}{r} \frac{dv}{dt} \qquad (2)$
Where
$\frac{dv}{dt}$ = Instantaneous Acceleration $(a)$
Now equation $(2)$ can be written as
$\alpha=\frac{a}{r}$
$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta v}{\Delta t} \rightarrow$ Instantaneous Acceleration $(a)$
$\frac{dv}{dt}$ = Instantaneous Acceleration $(a)$
Relation between angular velocity and linear velocity
Mathematical Relation between angular velocity $(\omega)$ and linear velocity$(v)$:
We know that the angular displacement of the particle is
$\Delta \theta= \frac{\Delta s}{r} \qquad(1)$
Where $r$ = The radius of a circle.
Now divide by $\Delta t$ on both side of equation $(1)$
$\frac{\Delta \theta}{\Delta t}=\frac{1}{r} \frac{\Delta s}{\Delta t} $
If $\Delta t \rightarrow 0$, then the above equation can be written as
$\underset{\Delta t \rightarrow 0}{Lim}\: \frac{\Delta \theta}{\Delta t}=\frac{1}{r}\: \underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta s}{\Delta t} \qquad(2)$
Where
$\underset{\Delta t \rightarrow 0}{Lim}\: \frac{\Delta \theta}{\Delta t}$ = Instantaneous Angular Velocity $(\omega)$
$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta s}{\Delta t}$= Instantaneous Linear Velocity $(v)$
Now equation $(2)$ can be written as
$\omega=\frac{1}{r}v$
$v=r\omega$
The above equation shows that linear or tangential velocity depends on the angular velocity and radius of the circular path. This means that if the radius of the circular path increases with the same angular velocity, then the linear velocity will also increase.
$\underset{\Delta t \rightarrow 0}{Lim}\: \frac{\Delta \theta}{\Delta t}$ = Instantaneous Angular Velocity $(\omega)$
Conservation's Law of linear momentum and its Derivation
Derivation of Conservation's law of Linear momentum from Newton's Second Law and Statement: Let us consider, A particle that has mass $m$ and is moving with velocity $v$ then According to Newton's second law the applied force on a particle is
Derivation of Conservation's law of Linear momentum from Newton's Third Law and Statement: Let us consider, The two-particle that have mass $m_{1}$ and $m_{2}$ are moving towards each other. If
The velocity of the particles $m_{1}$ before collision is = $u_{1}$
The velocity of the particles $m_{2}$ before collision is = $u_{2}$
The velocity of the particles $m_{1}$ after collision is = $v_{1}$
The velocity of the particles $m_{2}$ after the collision is = $v_{2}$
When these particles collide to each other than according to Newton's third law
$F_{12}=-F_{21}$
$m_{1}a_{1}=m_{2}a_{2}$
$m_{1}\frac{\Delta V_{1}}{\Delta t}=m_{2} \frac{\Delta V_{2}}{\Delta t} \quad (1) \qquad \left(\because a=\frac{\Delta V} {\Delta t} \right)$
Where
$\Delta V_{1}$= Change in Velocity of mass $m_{1}$ i.e $\left( v_{1}-u_{1} \right)$
$\Delta V_{2}$= Change in Velocity of mass $m_{2}$ i.e $\left( v_{2}-u_{2} \right)$
So from equation $(1)$
$m_{1}\frac{\left( v_{1}-u_{1} \right)}{\Delta t}=m_{2} \frac{\left( v_{2}-u_{2} \right)}{\Delta t}$
$m_{1}\left( v_{1}-u_{1} \right)=m_{2} \left( v_{2}-u_{2} \right)$
$m_{1} v_{1}- m_{1} u_{1}=m_{2}v_{2}- m_{2} u_{2}$
$m_{1} u_{1}+ m_{2} u_{2}=m_{1}v_{1} + m_{2} v_{2}$
From the above equation, we conclude the statement i.e.
| Derivation From General Form | Derivation from Differential Form |
|---|---|
|
$F=ma$
of the particle .i.e |
$F=ma$
|
From the above equation, we conclude the statement i.e.
When no external force is applied to a particle, the total momentum of a particle is always conserved.
The velocity of the particles $m_{1}$ before collision is = $u_{1}$
$\Delta V_{1}$= Change in Velocity of mass $m_{1}$ i.e $\left( v_{1}-u_{1} \right)$
$\Delta V_{2}$= Change in Velocity of mass $m_{2}$ i.e $\left( v_{2}-u_{2} \right)$
When two particle collide two each other. If the total momentum of the particles before the collision and total momentum of the particles after is collision is same then it is known as conservation law of linear momentum.
Alternating Current Circuit containing Capacitance only (C-Circuit)
Alternating Current Circuit Containing Capacitance Only (C-Circuit): Let us consider, A circuit containing a capacitor of capacitance $C$ only which is connected with an alternating EMF i.e electromotive force source i.e.
Let us consider, A circuit containing a coil of inductance $L$ only which is connected with an alternating EMF i.e electromotive force source i.e.
$E=E_{\circ}sin\omega t\qquad(1)$
When alternating emf is applied across the capacitor plates then the charge on capacitor plates varies continuously and correspondingly current flows in the connecting leads. Let the charge on the capacitor plates is $q$ and the current in the circuit at any instant is $i$. Since there is no resistance in the circuit then the instantaneous potential difference is $\frac{q}{C}$ across the capacitor plates must be equal to the applied emf i.e.
$\frac{q}{C} = E_{\circ} sin \omega t$
$q = CE_{\circ} sin \omega t \qquad(2)$
The instantaneous current $i$ in the circuit is, therefore
$i=\frac{dq}{dt} \qquad(3)$
Now substitute the value of $q$ from equation $(2)$ to equation $(3)$
$i=\frac{d}{dt} CE_{\circ} sin \omega t $
$i=CE_{\circ} \omega cos\omega t$
$i=\omega CE_{\circ} cos\omega t$
$i=\frac{E_{\circ}}{\frac{1}{\omega C}} cos\omega t$
$i=\frac{E_{\circ}}{X_{C}} cos\omega t$
Where $X_{C}= \frac{1}{\omega C}$ is known as capacitive reactance.
$i=i_{\circ} cos\omega t \qquad(4)$
Where the $i_{\circ}=\frac{E_{\circ}}{X_{C}}$ is the maximum current in the circuit. Now apply Ohm's law in this equation and we find that the term $X_{C}=\frac{1}{\omega C}$ has the dimension of resistance. It represents the 'effective opposition' of the capacitor to the flow of alternating current. It is known as the 'reactance of the capacitor' or 'capacitive reactance' and is denoted by $X_{C}$. The capacitive reactance is infinite for DC for which $f=0$.
$i=i_{\circ} sin \left( \omega t + \frac{\pi}{2} \right) \qquad(4)$
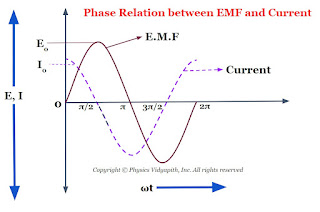
Now compare equation $(1)$ and equation $(4)$ which shows that an alternating circuit containing a capacitor only, the current leads the emf by a phase angle of $\frac{\pi}{2}$ or $90^\circ$ (or the emf lags behind the current by a phase angle of $\frac{\pi}{2}$). The phase diagram between EMF and the current of a capacitor is shown below-
The phasor diagram between the EMF and current of a capacitor is also shown in the given figure below-
Alternating Current Circuit containing Inductance only (L-Circuit)
Alternating Current Circuit Containing Inductance only (L-Circuit): Let us consider, An alternating current circuit containing a coil of inductance $L$ only. This inductor is connected with an alternating EMF i.e electromotive force source i.e.
$E=E_{\circ}sin\omega t\qquad(1)$
The current $i$ in coil varies continuously then an opposite emf is induced in the coil whose magnitude is $L\frac{di}{dt}$ So the net instantaneous of the circuit:
$E_{\circ}sin\omega t -L\frac{di}{dt}=0$
$E_{\circ}sin\omega t =L\frac{di}{dt}$
$di=\frac{E_{\circ}}{L}sin\omega dt$
Now integrate the above equation then the above equation can be written as
$\int di=\int \frac{E_{\circ}}{L}sin\omega dt$
$\int di= \frac{E_{\circ}}{L} \int sin\omega dt$
$i= \frac{E_{\circ}}{L} \frac{-cos\omega t}{\omega}$
$i= -\frac{E_{\circ}}{\omega L} cos\omega t$
$i= -\frac{E_{\circ}}{X_{L}} cos\omega t$
Where $X_{L}= \omega L$ is known as inductive reactance.
$i= -i_{\circ} cos\omega t$
Where $i_{\circ}=\frac{E_{\circ}}{X_{L}}$ is known as the maximum value of current in the circuit. Now compare this equation to Ohm's law then we find that the term $X_{L}=\omega L$ has the dimensions of resistance. It defines the 'effective opposition' of the coil to the flow of alternating current. it is known as the 'reactance of the coil' or 'inductive reactance' and it is denoted by $X_{L}$. The inductive reactance $X_{L}$ is zero for DC at which frequency is zero.
$i= -i_{\circ} sin \left(\frac{\pi}{2}- \omega t \right)$
$i= i_{\circ} sin \left(\omega t - \frac{\pi}{2} \right) \qquad(2)$
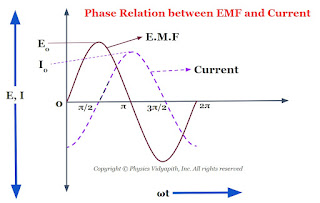
Now compare equation $(1)$ and equation $(2)$ which shows that an alternating circuit containing an inductor only, the current lags behind the emf by a phase angle of $\frac{\pi}{2}$ or $90^\circ$ (or the emf leads the current by a phase angle of $\frac{\pi}{2}$). The phase diagram between EMF and the current of an inductor is shown below-
The phasor diagram between the EMF and current of an inductor is also shown in the given figure below-
Electric field Intensity (Definition) and Electric field Intensity due to point charge
Definition of Electric Field Intensity:
Let us consider that a test-charged particle of $q_{0}$ Coulomb is placed at a point in the electric field and a force $F$ acting on them so the electric field intensity at that point
$ \overrightarrow{E}=\frac{\overrightarrow{F}}{q_{0}}$
SI Unit:$\quad Newton/Coulomb$ $ (N/C)$ $\quad Kg-m^{2}/sec^{3} A$
Dimension: $\left [ML^{2}T^{-3}A^{-1} \right ]$
Physical Significance of Electric Field:
The force experienced by a charge is different at different points in space. So electric field intensity also varies from point to point. In general, Electric field intensity is not a single vector quantity but it is a set of infinite vector and each point in space have a unique electric field intensity. So electric field is an example of the vector field.
Electric Field Intensity due to a Point Charge:
Let us consider that an isolated point charge of $+q$ Coulomb is placed at a point $O$ in a medium whose dielectric constant is $K$. If a test charge particle of $q_{0}$ Coulomb is placed at a point $P$ in the electric field at a distance $r$ from point $O$. So the electric field intensity (magnitude form) at point $P$
$E=\frac{F}{q_{0}}\qquad (1)$
According to Coulomb's Law:
$F=\frac{1}{4\pi \varepsilon _{0}K}\frac{qq_{0}}{r^{2}}\qquad (2)$
From equation $(1)$ and equation $(2)$, we can write
$E=\frac{1}{4\pi \varepsilon _{0}K}\frac{q}{r^{2}} \qquad (3)$
For air or vacuum $K=1$, Then from equation $(3)$
$E=\frac{1}{4\pi \varepsilon _{0}}\frac{q}{r^{2}} \qquad (4)$
Where
$\frac{1}{4\pi \varepsilon _{0}}=9\times10^{9} N-m^{2}/C^{2}$
From equation $(4)$
$E=9\times 10^{9} \frac{q}{r^{2}}\qquad (5)$
In Vector Notation:
$\overrightarrow{E}=\frac{1}{4\pi \varepsilon _{0}K}\frac{q}{r^{2}}r\hat{}$
If a system containing $'n'$ point charge $q_{1},q_{2},q_{3},..........q_{n}$ then electric field intensity due to the system of charge particle will be equal to the vector sum of the intensities i.e.
$\overrightarrow{E}=\overrightarrow{E_{1}}+\overrightarrow{E_{2}}+\overrightarrow{E_{3}}+....+\overrightarrow{E_{n}}$
$\overrightarrow{E}=\frac{1}{4\pi \varepsilon _{0}K}\sum_{i=0}^{n}\frac{q_{i}}{r_{i}^{2}}r_{i}\hat{}$
Where $r_{i}$ is the distance from point $'P'$ to charge $q_{i}$.
The force acting on the per unit test charge in electric field is called the Electric field intensity. It is represented by $'E'$.
 |
| Electric field intensity due to a point charge |
Refraction of light and its Properties
Definition of Refraction of light→
When a light goes from one medium to another medium then light bends from the path. This bending of the light phenomenon is knowns as the refraction of light.
When light goes from a rarer medium to a denser medium, light bends toward the normal as shown in the figure below:
When light goes from a denser medium to a rarer medium, the light goes away from normal as shown in the figure below.
Properties of refraction of light→
$\frac{sin \: i}{sin \: r}=constant(_{1}n_{2}) $
$\frac{sin \: i}{sin \: r}= (_{1}n_{2})$
$\frac{sin \: i}{sin \:r}=\frac{n_{2}}{n_{1}}$
Where $_{1}n_{2}$ is the refractive index of medium $(2)$ with respect to medium $(1)$ .
Absolute refractive index→
The ratio of the speed of light in a vacuum to the speed of light in a medium is called the absolute refractive index of the medium.
$refractive\: index(n)=\frac{speed\: of\:light\: in\: vacuum(c)}{speed \:of \:light\: in\: medium(v)}$
$n=\frac{c}{v}$
Note
According to Snell's law -
$\frac{sin \: i}{sin \: r}=\frac{n_{2}}{n_{1}} \quad\quad (1)$
$\frac{sin \: i}{sin \: r}=\frac{\frac{c}{v_{1}}}{\frac{c}{v_{2}}} \quad\quad \left \{ \because n=\frac{c}{v} \right \}$
$\frac{sin i}{sin r}=\frac{v_{1}}{v_{2}} \qquad (2)$
When the light goes from one medium to another medium frequency of the light does not change but the wavelength of the light changes. So above given equation can be written as
$\frac{sin \: i}{sin \: r}=\frac{\nu \lambda_{1}}{\nu \lambda_{2}} \quad\quad \left \{ \because v=\nu \lambda \right \} $
$\displaystyle \frac{sin \: i}{sin \: r}=\frac{\lambda_{1}}{ \lambda_{2}} \qquad (3)$
From equation $(1)$ ,equation $(2)$, and equation $(3)$ we can write the equation
$\frac{sin \: i}{sin \: r}=\frac{n_{2}}{n_{1}} =\frac{v_{1}}{v_{2}}= \frac{\lambda_{1}}{ \lambda_{2}}$
Conditions for a light ray to pass undeviated on refraction of light→
A ray of light passes undeviated from medium $1$ to medium $2$ in either of the following two conditions:
Factors affecting the refractive index of the medium→
The refractive index of a medium depends on basically following three factors:
1. Nature of the medium (on the basis of speed of light)→
Less the speed of light in the medium as compared to that in the air more is the refractive index of the medium.
$\left ( n=\frac{c}{v}\right)$
Speed of light in glass- $v_{glass} = 2\times 10^{6} ms^{-1}$
$\mu_{glass} = 1\cdot 5$
Speed of light in water- $v_{water} = 2\cdot25\times10^8ms^{-1}$
$\mu_{water} = 1\cdot33$
2. Physical conditions such as temperature→
With the increase in temperature, the speed of light in the medium, so the refractive index of the medium decreases.
3. The colour or wavelength of light→
The speed of light of all colours is the same in the air ( or vacuum), but in any other transparent medium, the speed of light is different for different colours. In a given medium the speed of red light is maximum and that of the violet light is least, therefore the refractive index of that medium is maximum for violet is and least for red light i.e. $\left ( \ n_{violet}> n_{red}\right )$. The wavelength of visible light increase from violet to red end, so the refractive index of a medium decreases with the increases in wavelength.
 |
| Propagation of light from rarer medium to denser medium |
 |
| Propagation of light from denser medium to rarer medium |
- The incident ray, normal ray, and refracted ray lie on the same point.
- According to Snell's law - The ratio of the sine of the incident angle to the sine of the refractive angle is always constant. This constant value is known as the refractive index of the medium.
- When the angle of incidence at the boundary of two media is zero $\angle i =0^{\circ} so \ \angle r= 0^{\circ}$.
- When the refractive index of the medium (2) and medium (1) is the same i.e. $i=r$.
Alternating Current Circuit containing Resistance only (R-Circuit)
Alternating Current Circuit containing Resistance (R-Circuit): Let us consider, An alternating current circuit containing resistance $R$ only. This resistance $R$ is connected with an alternating EMF i.e electromotive force source i.e.
$E=E_{\circ}sin\omega t\qquad(1)$
The potential difference across the circuit
$E=iR$
Then from equation $(1)$
$iR=E_{\circ}sin\omega t $
$i=\frac{E_{\circ}}{R}sin\omega t $
$i=i_{\circ}sin\omega t \qquad(2) $
Where $i_{\circ}$ is the peak value or amplitude of the current in the circuit which has value $i_{\circ}=\frac{E_{\circ}}{R}$.
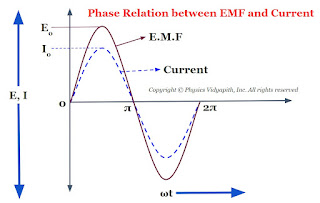
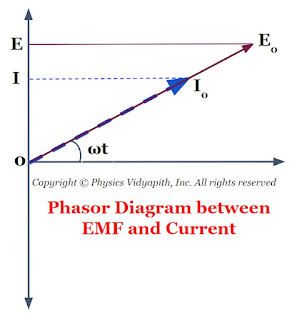
Now compare the equation $(1)$ and equation $(2)$ which shows that if a circuit is containing a resistor only then the current is always in phase with the applied EMF i.e electromotive force. The phase diagram between EMF and the current of resistance is shown below-
The phasor diagram between the EMF and current of resistance is also shown in the given figure below-
Derivation of Addition of Velocity in Special Relativity
Addition of Velocities:
Let us consider two frames $S$ and $S'$, frame $S'$ is moving with constant velocity $v$ relative to frame $S$ along the positive direction of the X-axis.
Let us express the velocity of the body in these frames. Suppose that body moves a distance $dx$ in time $dt$ in frame $S$ and through a distance $dx'$ in the time $dt'$ in the system $S'$ from point $P$ to $Q$. Then
$\frac{dx}{dt} = u\qquad \frac{dx'}{dt'}= u'\qquad (1)$
From Lorentz's inverse transformation
$x=\alpha\left ( x'+vt' \right )\qquad(2)$
$t=\alpha '\left ( t'+\frac{v\cdot x'}{c^{2}} \right )\qquad(3)$
Differentiate the equation $(2)$ and equation $(3)$ with respect to $t'$
$\frac{dx}{dt'}= \alpha \left ( \frac{dx'}{dt'}+v \right )\qquad(4)$
$\frac{dt}{dt'}= \alpha ' \left ({1}+\frac{v}{c^{2}} \cdot \frac{dx'}{dt'} \right )\quad (5)$
Now divide the equation $(4)$ by equation $(4)$. So
$\frac{\frac{dx}{dt'}}{\frac{dt}{dt'}} = \left ( \frac{\frac{dx'}{dt}+v}{1+\frac{v}{c^{2}}\cdot \frac{dx'}{dt'} } \right ) \qquad $
From Lorentz Transformation $\alpha =\alpha '$. So above equation can be written as:
$\frac{dx}{dt} = \frac{u' +v}{1+ \frac{u'v}{c^{2}}}$
From equation $(1)$. The above equation can be written as:
$u = \frac{u' +v}{1+ \frac{u'v}{c^{2}}} $
This equation represents the relativistic law of addition of velocities with respect to an observer at frame-$S$ whereas in classical mechanics it is simply $u = u'+v$. There is the following point observed from the addition of the velocities equation.
 |
| Addition of velocity |
- When $u'$ and $v$ are the smaller as compare to $c$, then $\frac{v\cdot u'}{c^{2}}$ can be negligible so
$u = u'+v$which is classical formula.
- When $u' = c$Then $u =\frac{c+v}{1+\frac{v}{c}}$ So,
$u=c$Therefore a object moves with velocity of light $c$ with respect to other, then their relative velocity is always $c$.
- When $v=u'=c$Then $u =\frac{c+c}{1+\frac{c^{2}}{c^{2}}}=c$ So,
$u=v$This shows that the addition of the velocity of light simply reproduces the velocity of light. It means that the velocity of light in a vacuum is the maximum achievable velocity in nature and no signal and any object can travel faster than the velocity of light in a vacuum.
Work done by a rotating electric dipole in uniform electric field
Derivation of Work done by a rotating electric dipole in uniform electric field :
Let us consider, An electric dipole AB, made up of two charges $+q$ and $-q$, is placed at a very small distance $2l$ in a uniform electric field $\overrightarrow{E}$. If dipole $AB$ rotates at angle $θ$ from its equilibrium position. If $A'$ and $B'$ are the new position of a dipole in the electric field. Then force on $+q$ charge particle due to electric field→
$ \overrightarrow{F_{+q}}=q\overrightarrow{E}\qquad (1)$
Then force on $-q$ charge particle due to electric field→
$ \overrightarrow{F_{-q}}=q\overrightarrow{E}\qquad(2)$
So work done by a force on $+q$ charge particle to bring from position $A$ to position $A'$→
$ \overrightarrow{W_{+q}}=\overrightarrow{F_{+q}}·\overrightarrow{AC}$
$ \overrightarrow{W_{+q}}=q\overrightarrow{E}· \overrightarrow{AC}\qquad(3)$
Similarly, work done by the force on $-q$ charge particle to bring from position $B$ to position $B'$→
$ \overrightarrow{W_{-q}}=\overrightarrow{F_{-q}}·\overrightarrow{BD}$
$ \overrightarrow{W_{-q}}=q\overrightarrow{E}· \overrightarrow{BD}\qquad (4)$
So the total work is done by the force on the dipole→
$ \overrightarrow{W}=\overrightarrow{W_{+q}}\:+\:\overrightarrow{W_{-q}}$
$\overrightarrow{W}=q\overrightarrow{E}·(\overrightarrow{AC}+\overrightarrow{BD})\qquad (5)$
From the figure, There is symmetry so
$ \overrightarrow{AC}=\overrightarrow{BD}$
So from equation $(5)$
$ \overrightarrow{W}=q\overrightarrow{E}·(2\overrightarrow{AC})$
$ \overrightarrow{W}=2q\overrightarrow{E}(\overrightarrow{AO}-\overrightarrow{CO})\qquad (6)$
From figure→
$ \left | \overrightarrow{AO} \right |=l$
$ \left | \overrightarrow{CO} \right |=l\:cos \theta$
Now substitute the values in equation (6). So equation (6) can be written as in magnitude form →
$ W=2qE(l-l\:cos\theta )$
$ W=2qEl(1-cos\theta )$
$ W=pE(1-cos\theta )$
The above expression shows that work is done on a rotating electric dipole in a uniform electric field.
Case (i):
If $\theta=0^{\circ}$, Then work done will be minimum
$W_{min}=0$
Case (ii):
If $\theta=90^{\circ}$, Then work done
$W=pE$
Case (iii):
If $\theta=180^{\circ}$, Then work done will be maximum
$W_{max}=2pE$
 |
| Work done by rotating an electric dipole |
Electric field Intensity due a uniformly charged Spherical Shell
Electric field intensity at a different point in the field due to the uniformly charged spherical shell:
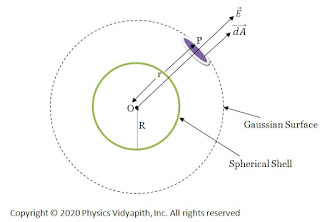
Let us consider, a spherical shell of radius $R$ in which $+q$ charge is distributed uniformly on the surface of the sphere. Now find the electric field intensity at different points due to the spherical shell. These different points are:
1.) Electric field intensity at an external point of the spherical shell
2.) Electric field intensity on the surface of the spherical shell
3.) Electric field intensity at an internal point of the spherical shell
1. Electric field intensity at an external point of the spherical shell:
If point $O$ is the center of the spherical shell, The electric field at the outside of the spherical shell can be determined by the following steps →
1.) First, take the point $P$ outside the sphere
2.) Draw a spherical surface of radius r which passes through point $P$.This hypothetical surface is known as the Gaussian surface.
3) Now take a small area $\overrightarrow {dA} $ around point $P$ on the Gaussian surface to find the electric flux passing through it.
4.) Now find the direction between the electric field vector and small area vector.
Due to uniform charge distribution, the electric field intensity will be the same at every point on the Gaussian surface. So from the figure,
The direction of electric field intensity on the Gaussian surface is radially outward which is in the direction of the area vector of the Gaussian surface. i.e. ($\theta=0^{\circ}$).Here $\overrightarrow {dA}$ is small area around point $P$ so the small electric flux $d\phi_{E}$ will pass through this small area $\overrightarrow {dA}$. so this flux can be found by applying the Gauss's law in question given below:
$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$
$ d\phi_{E}= E\:dA\: cos 0^{\circ} \qquad \left \{\because \theta=0^{\circ} \right \}$
$ d\phi_{E}= E\:dA \qquad (1) \quad \left\{\because cos0=1 \right \}$
The electric flux passing through the entire Gaussian surface, So integrate the equation $(1)$ →
$ \phi_{E}=\oint E\:dA\qquad(2)$
According to Gauss's law:
$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$
From equation (1) and equation (2), we can write as
$ \frac{q}{\epsilon_{0}}=\oint E\:dA$
$ \frac{q}{\epsilon_{0}}= E\oint dA$
The area of entire Gaussian spherical is $\oint {dA}=4\pi r^{2}$. Now substitute this value in above equation. So above equation can be written as:
$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$
$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}$
From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged spherical shell is the same as, like the entire charge is placed at the center, point charge
If the surface charge density is $\sigma$, Then total charge $q$ on the surface of a spherical shell is →
$ q=4\pi R^{2}\: \sigma$
Substitute this value of charge $q$ in above equation, so we can write the equation as:
$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi R^{2}\: \sigma}{r^{2}}$
$ E=\frac{\sigma}{\epsilon_{0}}\frac{R^{2}}{r^{2}}$
This equation describes the electric field intensity at the external point of the spherical shell.
2. Electric field intensity on the surface of the spherical shell:
If point $P$ is placed on the surface of the spherical shell i.e ($r=R$). so electric field intensity on the surface of the spherical shell can be found by putting $r=R$ in the formula of the electric field intensity at the external point of the spherical shell:
$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{R^{2}}$
$ E=\frac{\sigma}{\epsilon_{0}}$
3. Electric field intensity at an internal point of the spherical shell:
If point $P$ is placed inside the spherical shell then the electric field intensity will be zero at that point because the charge is distributed uniformly on the surface of the solid sphere so there will not be any charge on the Gaussian surface and electric flux will be zero inside the solid sphere. i.e.
$ \phi_{E}=\oint E\:dA$
$ 0=E\oint dA \qquad \left \{ \because \phi_{E}=0 \right \}$
$ E=0$
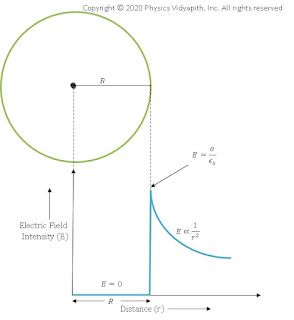
Electric field intensity distribution with distance for Spherical Shell:
Electric field intensity distribution with distance shows that the electric field is maximum on the surface of the sphere and zero inside the sphere. Electric field intensity distribution outside the sphere reduces with the distance according to $E=\frac{1}{r^{2}}$.
2.) Electric field intensity on the surface of the spherical shell
3.) Electric field intensity at an internal point of the spherical shell
2.) Draw a spherical surface of radius r which passes through point $P$.This hypothetical surface is known as the Gaussian surface.
3) Now take a small area $\overrightarrow {dA} $ around point $P$ on the Gaussian surface to find the electric flux passing through it.
4.) Now find the direction between the electric field vector and small area vector.
 |
| Electric field intensity due to the uniformly charged |
 |
| Electric field intensity distribution with distance |
Popular Posts
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(10)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(1)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(4)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(1)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(33)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)






%20and%20linear%20velocity%20(%E2%8D%B5).jpg)