Difference between Potentiometer and Voltmeter

There are the following differences between a potentiometer and a voltmeter given below:

Potentiometer:

1.) It is based on null method.

2.) It gives an accurate value of emf.

3.) While measuring emf, it does not draw any current from the cell.

4.) Resistance of potentiometer wire becomes infinite while measuring emf.

5.) It can be used for various experimental purposes.

6.) It can not be taken conveniently from one place to another place.

Voltmeter:

1.) It is based on the deflection method.

2.) It does not give an accurate value of emf.

3.) While measuring emf, it draws some current from the cell. Hence it reads slightly less than the actual emf.

4.) The resistance of the voltmeter is high enough but not infinite.

5.) It can be used to measure potential differences only.

6.) It can be conveniently taken from one place to another place.

Read More

Principle Construction, Working and Angular Magnification of Simple Microscope

Principle of Simple Microscope:

The principle of the simple microscope is based on the magnification of an image by using a simple convex lens.

Construction:

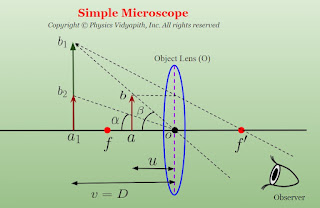
A simple microscope consists of one convergent lens only. The object is placed between the lens and its focal length, and the eye is placed just behind the lens. Then the eye sees a magnified, erect, and virtual image on the same side as the object at the least distance of distinct vision $(D)$ from the eye, and the image is then seen most distinctly.

Working:

If the small object $ab$ is placed between a lens $O$ and its first focus $f$ then Its magnified virtual image $a_{1}b_{1}$ is formed at a distance $D$ from the lens. Since the eye is just behind the lens, the distance of image $a_{1}b_{1}$ from the eye is also $D$.

Angular Magnification Or Magnifying Power($M$):

The ratio of the angle subtended by the image at the eye ($\beta$) to the angle subtended by the object at the eye when placed at the least distance of distinct vision ($\alpha$) is called the angular magnification or magnifying power.

$M= \frac{Angle \: subtended \: by \: the \: image \: at \: the \: eye \: (\beta)}{Angle \: subtended \: by \: the \: object \: at \: the \: eye \: when \\ placed \: at \: least \: distance \: of \: distinct \: vision \: (\alpha)}$

$M=\frac{\beta}{\alpha} \approx \frac{tan \beta}{tan \alpha} \quad (1)$

From figure

$tan \beta = \frac{ab}{oa} $

$tan \alpha = \frac{a_{1}b_{2}}{a_{1}o}$

Here $a_{1}b_{2} = ab$

$tan \alpha = \frac{ab}{a_{1}o}$

Now substitute these values in equation $(1)$, then

$M=\frac{\frac{ab}{ao}}{\frac{ab}{a_{1}o}}$

$M=\frac{a_{1}o}{ao}$

Here $ao = u$ (Distance between object and optical center of the lens) and $a_{1}o = D$ (Least Distance of distinct vision), then the above equation can be written as

$M=\frac{D}{u} \qquad(2)$

We know that the lens formula $\frac{1}{v}-\frac{1}{u} = \frac{1}{f}$

Now put
$v=-D$ (The image $a'b'$ is being formed at a distance $D$ from lens)
$u=-u$

$\frac{1}{-D}-\frac{1}{-u} = \frac{1}{f}$

Multiply $D$ in the above equation

$-\frac{D}{D}-\frac{D}{-u} = \frac{D}{f}$

$-1-\frac{D}{-u} = \frac{D}{f}$

$\frac{D}{u} =1 + \frac{D}{f} \qquad(3)$

From equation $(2)$ and equation $(3)$, then

$M=1 + \frac{D}{f} $

If eye is kept at distance $d$ from lens then $v=-(D-d)$, and the magnifying power will be

$M=1+\frac{D-d}{f}$

To see with a relaxed eye, the image $a'b'$ should be formed at infinity. In this case, the object $ab$ will be at the focus of the lens, i.e. $u=f$ then magnifying power

$M= \frac{D}{f} $

Read More

Origin of Biomedical Signals

The biomedical signals differ from other signals only in terms of the application — signals that are used in the biomedical field. As such, biomedical signals are produced from a variety of sources. The following is a brief description of these sources:

1. Bioelectric signals: The bioelectric signal is unique to biomedical systems. It is produced by nerve cells and muscle cells. It is produced due to the membrane potential, which under certain conditions may be excited to generate an action potential. In single-cell measurements, the specific microelectrodes are used as sensors, and the action potential itself is considered as the biomedical signal. In more gross measurements, the surface electrodes are used as sensors, and the electric field generated by the action of many cells, distributed in the electrode’s vicinity, constitutes the bioelectric signal. Bioelectric signals are probably the foremost biosignals. The fact that most biosystems use excitable cells makes it possible, to use biosignals to study and monitor the main functions of the systems. The electric field propagates through the biological medium, and thus the potential may be acquired at relatively convenient locations on the surface, eliminating the need to invade the system. The bioelectric signal is acquired by a relatively simple transducer. A transducer is required in the field of biomedical because the electric conduction in the biomedical medium is executed through ions, while the conduction in the measurement system is executed through electrons. All these lead to the fact that the bioelectric signal is broadly used in most of the fields of biomedicine.

2. Bioimpedance signals: The impedance of the tissue contains important information related to its composition, blood volume, blood distribution, endocrine activity, autonomic nervous system activity, and many more. The bioimpedance signal is usually generated by injecting into the tissue under test sinusoidal currents (frequency range of $50 kHz–1 MHz$, with low current densities of the order of $20–20 mA$). The electrode polarization problems are minimized by choosing the frequency range and the low current densities are selected to prevent tissue damage mainly due to heating effects. Bioimpedance measurements are usually performed with four electrodes. Two electrodes (known as source electrodes) are used to inject the current into the tissue and these electrodes are connected to a current source. Remaining two electrodes (known as measuring electrodes) are placed on the tissue under investigation and used to measure the voltage drop generated by the current and the tissue impedance.

3. Bioacoustic signals: Many biomedical phenomena create acoustic noise. The measurement of this acoustic noise gives information about the underlying phenomenon. The flow of blood in the heart (i.e through the heart’s valves, or through blood vessels) generates typical acoustic noise. The flow of air through the upper and lower airways and in the lungs generates acoustic sounds. These sounds are called coughs, snores, and chest and lung sounds. These sounds are used extensively in medicine. Sounds are also produced in the digestive tract and in the joints. It also has been observed that the contracting muscle generates an acoustic noise or muscle noise. Since the acoustic energy propagates through the biological medium, the bioacoustic signal may be conveniently acquired on the surface, using acoustic transducers (microphones or accelerometers).

4. Biomagnetic signals: Many organs, such as the brain, heart, and lungs, produce extremely weak magnetic fields. The measurements of these fields provide information but are not included in other biosignals (such as bioelectric signals). Due to the low level of the magnetic fields to be measured, biomagnetic signals are usually of a very low signal-to-noise ratio. Extreme precautions must be taken in designing or developing the acquisition system of these signals.

5. Biomechanical signals: The term biomechanical signals includes all signals used in the biomedicine fields that originate from some mechanical function of the biological system. These signals include motion and displacement signals, pressure and tension signals, flow signals, and others. The measurement of bio-mechanical signals requires a variety of transducers, not always simple and inexpensive. The mechanical phenomenon does not propagate in biomedical signals, as do the electric, magnetic, and acoustic fields. Hence the measurement usually has to be performed at the exact site. This very frequently complex the measurement and forces it to be an invasive one.

6. Biochemical signals: The chemical measurements from the living tissue or from samples analyzed in the clinical laboratory produce biochemical signals. Measuring the concentration of various ions inside and around a cell using specific ion electrodes. It is an example of such a signal. Partial pressures of oxygen (pO2) and carbon dioxide (pCO2) in the blood or respiratory system are other examples. Biochemical signals are often very low-frequency signals. Mostly, biochemical signals are actually DC signals.

7. Biooptical signals: Bio-optical signals are the result of optical functions of the biological system, occurring naturally or induced by the measurement. Blood oxygenation may be analyzed by measuring the transmitted and backscattered light from a tissue ( i.e.in vivo and in vitro) in several wavelengths. Important information about the fetus may be acquired by measuring the fluorescence characteristics of the amniotic fluid. Analysis of the Heart output may be performed by the dye dilution method, which requires the observation of the appearance of recirculated dye in the bloodstream. The development of fiberoptic technology has opened vast applications of bio-optical signals.

Read More

Principle Construction, Working and Angular Magnification of Compound Microscope

Principle: The principle of the compound microscope is based on the magnification of an image by using two lenses.

Construction: A compound microscope consists of two convergent lenses (i.e. objective lens $O$ and eye-piece lens $e$) placed coaxially in a double tube system. The objective lens is an achromatic convergent lens system of short focal length and short aperture. The other eye-piece lens $e$ is also an achromatic convergent lens system of large focal length and large aperture. The observation is taken through the eye-piece lens by the observer. The eye-piece lens is fitted outer side of a movable tube and the inner side connects with a non-movable tube in which the objective lens is fitted on another side of the non-movable tube. The separation between the objective or eye-piece lens can be changed by an arrangement, this is known as rack and pinion arrangement.

Working: Suppose a small object $ab$ is placed slightly away from the first focus $f_{\circ}$ of the objective lens which forms a real, inverted, and magnified image $a_{1}b_{1}$. Now adjust the eye-piece lens by moving like this, that the image $a_{1}b_{1}$ lies in between the optical center and the second focal length $f_{e}$ of the eye-piece lens. This image $a_{1}b_{1}$ works as an object for the eye-piece lens which forms a magnified, virtual, and final image $a_{2}b_{2}$. The final image $a_{2}b_{2}$ is generally formed at the least distance $D$ of distinct vision, although it can be formed anywhere between this position and infinity.

Angular Magnification Or Magnifying Power($M$):

The angular magnification or magnifying power can be defined as the ratio of the angle subtended by the image at the eye ($\beta$) to the angle subtended by the object at the eye when placed at least distance of distinct vision ($\alpha$)

$M= \frac{Angle \: subtended \: by \: the \: image \: at \: the \: eye \: (\beta)}{Angle \: subtended \: by \: the \: object \: at \: the \: eye \: when \\ placed \: at \: least \: distance \: of \: distinct \: vision \: (\alpha)}$

$M=\frac{\beta}{\alpha} \approx \frac{tan \beta}{tan \alpha} \quad (1)$

From figure

$tan \beta = \frac{a_{2}b_{2}}{a_{2} e} $

$tan \alpha = \frac{a_{2}a_{3}}{a_{2}e}$

Now subtitute these values in equation $(1)$, then

$M=\frac{\frac{a_{2}b_{2}}{a_{2} e}}{\frac{a_{2}a_{3}}{a_{2}e}}$

$M=\frac{a_{2}b_{2}}{a_{2}a_{3}}$

Here $a_{2}a_{3} = ab$

So the above equation can be written as

$M=\frac{a_{2}b_{2}}{ab}$

$M=\frac{a_{2}b_{2}}{ab} \frac{a_{1}b_{1}}{a_{1}b_{1}}$

$M=\frac{a_{2}b_{2}}{a_{1}b_{1}} \frac{a_{1}b_{1}}{ab}$

Here $m_{e}=\frac{a_{2}b_{2}}{a_{1}b_{1}}$ and $m_{\circ}= \frac{a_{1}b_{1}}{ab}$

Now substitute the values of $m_{e}$ and $m_{\circ}$ in the above equation

$M=m_{e} \times m_{\circ} \qquad(1)$

Where
$m_{e} \rightarrow$ The linear magnification produced by eye-piece lens system
$m_{\circ} \rightarrow$ The linear magnification produced by the object lens system

So now again from the figure

The linear magnification produced by object lens system $m_{\circ} = -\frac{v_{\circ}}{u_{\circ}}$

The linear magnification produced by eye-piece lens system $m_{e} = \frac{D}{u_{e}}$

Substitute the value of $m_{\circ}$ and $m_{e}$ in equation $(1)$

$M= -\frac{v_{\circ}}{u_{\circ}} \left( \frac{D}{u_{e}} \right) \qquad(2)$

Adjustment of a Compound Microscope:

1.) Adjustment for Clear Vision: In this final image an object is formed at least a distance of distinct vision $D$. For this configuration,

On substitution $u=-u_{e}$, $v=-D$ and $f=f_{e}$ in the lens formula for eyepiece lens

$\frac{1}{-D}+\frac{1}{u_{e}}=\frac{1}{f_{e}}$

$\frac{1}{u_{e}}=\frac{1}{f_{e}} + \frac{1}{D}$

$\frac{D}{u_{e}}= \left( \frac{D}{f_{e}} + 1 \right)$

Now substitute the value of $\frac{D}{u_{e}}$ in equation $(2)$

$M= -\frac{v_{\circ}}{u_{\circ}} \left(1+ \frac{D}{f_{e}} \right) $

The length of the microscope tube in this setup

$L=$ Distance between the object and the eye-piece lenses

$L= v_{\circ} + |u_{e}|$

2.) Adjustment for Relaxed Eye: In this configuration, the final image of an object is formed in a relaxed eye position i.e. at $\infty$. In this setup, the eye-piece lens system is moved back until the image of object $ab$, formed by object lens,i.e., $a_{1}b_{1}$ fall at (coincide with)second focus $f'_{e}$ of the eye-piece lens system. Mathematically this situation comes when $u_{e} = f_{e}$

Thus, the magnifying power in this position,

$M=-\frac{v_{\circ}}{u_{\circ}} \left( \frac{D}{f_{e}} \right)$

For this set the length of the microscope tube,

$L=v_{\circ}+f_{e}$

Read More

Nanoparticles and Its Properties

Introduction:

The prefix 'nano' means a billionth ($10^{-9}$). The field of nanotechnology is the study of various structures of matter having dimensions of the order of a billionth of a meter. These particles are called nanoparticles. Nanotechnology is based on the fact that particles that are smaller than about $100 nm$ give rise to new properties of nanostructures built from them.

Particles that are smaller than the characteristic length for a particular phenomenon show different physical and chemical properties than particles of larger sizes. For example, mechanical properties, optical properties, conductivity, melting point, and reactivity have all been observed to change when particles become smaller than the characteristic length.

Gold and silver nanoparticles were used in window glass panes to obtain a variety of beautiful colors. Nanotechnology has a wide range of applications like producing lighter but stronger materials, constructing faster switches for computers, improving drug delivery to specific organs of the body, etc.

The radii of atoms and most of the molecules are less than a nanometer. Nanoparticles are generally considered to have a radius in the range of $1 nm$ to $100 nm$ which can have $25$ to $10^{6}$ atoms. A cluster of $1 nm$ radius has approximately $25$ atoms. This definition of nanoparticles based on size does not distinguish between molecules and nanoparticles as many organic molecules contain more than $25$ atoms.

Nanoparticles can be more appropriately defined as an aggregate of atoms, with a radius between 1 nm and 100 nm, with dimensions less than the characteristic length of some physical phenomena.

When particle size is less than the characteristic length of some physical phenomena, the particles show different properties. The nanoparticles show unique properties that change with their size. Classical mechanics is able to explain the properties of bulk materials but is unable to explain the properties of nanoparticles. Quantum mechanical principles have to be used to explain the properties of the nanoparticles.

Properties of Nanoparticles

As discussed earlier, the properties of nanoparticles are different from the bulk material. The properties of nanoparticles also vary with size and shape. Hence different properties can be obtained by changing the size and shape of the nanoparticles. Some of the properties of nanoparticles are as follows :

1) Optical properties: The color of nanoparticles is different from the bulk material. When a bulk material is reduced in size to a few hundred atoms, the energy band structure of the bulk material changes to a set of discrete energy levels. Atomic clusters of different sizes will have different energy level separations. As clusters of different sizes have different energy level separations, the color of the clusters (which are due to transitions between the energy levels) will depend on their size. Hence the size of the cluster can be altered to change the colour of a material. For example, gold in bulk form appears yellow but gold nanoparticles appear bright red in color. The medieval glass makers produced tinted glass with a beautiful variety of colors by dissolving metal particles like gold, silver, cobalt, iron, etc. Due to these metal nanoparticles, the glasses appear colored.

In semiconductor nanoparticles (which are used in quantum dots) there is a significant shift in the optical absorption spectra towards blue as the particle size is reduced.

2) Electrical properties: The resistivity in bulk matter is mainly due to the scattering of electrons by ions and crystal defects. In nanostructures, the resistivity mainly depends on scattering from the boundaries of nanoparticles when particle size becomes less than the mean free path between collisions. Thus smaller particle size increases the resistivity.

Various types of defects in the lattice also increase the resistivity by limiting the mean free path. However many nanostructures are too small to have internal defects.

Another effect of reduced size is the confinement of conduction electrons. In bulk conductors, the electrons move freely throughout the entire conductor. The situation changes when one or more dimensions of the conductor are made very small.

Consider a flat conducting plate with a large length and width but a small thickness in the range of a few nanometers. In this configuration, called a quantum well, the electron will be confined along one dimension but will move freely along the remaining two dimensions.

If a conducting wire has a long length but a very small diameter, the electrons can move freely along the length but will be confined in two mutually perpendicular transverse directions. This configuration is known as a quantum wire.

If all three dimensions of the conductor are in nanometer range, the configuration is called a quantum dot and the electron is confined in all three dimensions. Confinement of electrons to small dimensions leads to quantization of energy.

The level of doping in semiconductors gives rise to another important phenomenon. For typical doping levels of 1 donor impurity atom in $10^{8}$ atoms of semiconductor atoms, a quantum dot of $10^{7}$ semiconductor atoms would have an average of $10^{-1}$ electrons. In other words, on an average, one quantum dot in 10 will have a free electron. These result in the phenomena of single-electron tunneling and coulomb blockade. The conduction is due to the tunneling of electrons through the quantum dot. The electrons are blocked from tunneling except at discrete voltage change positions. This phenomenon is called coulomb blockade. The I-V characteristic shown in the above Figure is called the coulomb staircase.

3) Magnetic properties: Magnetic properties are basically due to the orbital and spin motions of electrons around the nucleus. Every electron in an atom has spin and orbital magnetic moment which, when added, gives the total magnetic moment of the electron. The vector sum of all the moments of electrons gives the total moment of the atom. In most of the atoms, the net magnetic moment is zero.

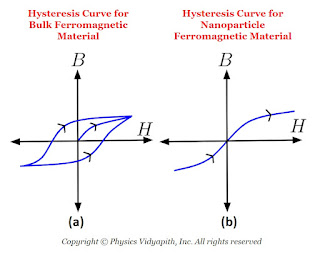
However, atoms like iron, cobalt, and manganese, have a net magnetic moment. Crystals of these become atoms ferromagnetic when magnetic moments of all atoms are aligned in the same direction. The magnetic moment of magnetic nanoparticles is observed to be less than the value for perfect alignment of all moments. The net magnetic moment is observed to decrease with increasing temperature. This is due to thermal vibration of atoms in the cluster which disturbs the alignment of magnetic moments.

In bulk ferromagnetic materials, the magnetic moment is less than the moment the material would have if every atomic moment were aligned in the same direction. This is due to the presence of 'domains' which are regions in which all atomic moments are in one direction but moments of different domains are in different directions. When bulk ferromagnetic materials are subjected to alternating magnetic fields, they show hysteresis for which the B-H curve is shown in the above Figure (a). In nanosized ferromagnetic particles, essentially consisting of a single domain, there is no hysteresis and the $B-H$ curve is as shown in the above Figure (b). These particles are called the superparamagnetic.

The saturation magnetization is observed to increase significantly on decreasing the particle size. Another interesting property of nanoparticles is that clusters made of up nonmagnetic atoms like rhenium show magnetic moment which increases with the decrease in particle size.

4) Structural properties: The structure of small nanoparticles can be entirely different from that of the bulk material. The crystal structure of large nanoparticles is observed to be the same as the bulk material but with different lattice parameters. As a result of the changed structure, the electronic structure changes which in turn leads to changes in optical properties and reactivity. (TWD)

5) Mechanical properties: Mechanical properties like hardness, elasticity, and ductility depend upon the bonds between atoms. Imperfections in the crystal structure and impurities result in changes in these properties. As the nanoparticles are highly pure and free from imperfections, they show different mechanical properties than the bulk material. It has been observed that Young's modulus decreases in metallic nanocrystals with a decrease in particle size. The yield stress has been observed to increase with the decrease in grain size in bulk materials with nanosized grains. Hence stronger materials can be produced by making materials with nanosized grains. The carbon nanotubes are estimated to be about 20 times stronger than steel.

Read More

Difference Between Prism Spectra and Grating Spectra

Prism Spectra

1.) Prism spectra are obtained by the phenomena of dispersion of light.

2.) Prism spectra have only one order.

3.) A prism spectrum is of bright intensity.

4.) In prism spectra, spectral colors overlap each other.

5.) Red color is dispersed least whereas violet color disperses the maximum.

6.) Prism spectrum depends upon the material of prism.

7.) The prism spectral lines are curved.

. Grating Spectra

1.) Grating spectra are obtained by the phenomena of diffraction of light.

2.) Grating spectra has more than one order.

3.) Grating spectra is of less intensity.

4.) In grating spectra, there is no overlapping of color.

5.) Red color diffracts the maximum whereas violet color diffracts the least.

6.) Grating spectra are independent of the material of grating.

7.) The grating spectral lines are almost straight.

Read More

Difference between interference and diffraction

Interference

1.) It is due to the superposition of two or more than two wavefronts coming from coherent sources.

2.) The intensity of all bright fringes are same

3.) Interference fringes either of the same size or decrease after moving away from the center.

4.) Dark fringes are usually perfectly dark.

5.) A minimum coherent source is needed.

Diffraction:

1.) It occurs due to secondary wavelets, originating from infinite different points of the same wavefronts.

2.) Central maxima of bright fringe is followed by either side maxima of decreasing intensity.

3.) Interference fringes are never of the same shape and size.

4.) Dark fringes are not perfectly dark.

5.) It is possible by either one or more than one source which need not be coherent.

Read More