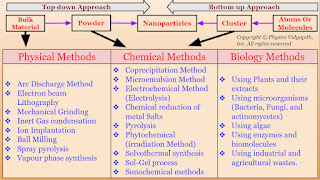
In the field of nanomaterials, there are two main approaches to their synthesis and fabrication.
A.) Top-Down Approach
B.) Bottom-up Approach
These two approaches are based on the methods used to create or assemble nanoscale materials and structures.
A.) Top-Down Approach: In this approach, large-scale materials (i.e. Bulk materials) are broken down into smaller and smaller components until they reach the desired nanoscale dimensions i.e. firstly the bulk material is converted into powder form and then the powder's form is converted into nanoparticles. There are various physical methods (like Arc discharge method, Electron beam lithography, Mechanical grinding, etc) used to convert the bulk material into powder form and powder form is converted into nanoparticles by chemical methods (like Sol-Gel Process, Electrochemical method, Microemulsion etc.).
One of the challenges with the top-down approach is that it may lead to a lack of control over the final nanomaterial's properties and may also generate waste during the process.
Top-down approaches are based on grinding the material. Thus these processes are subtractive in nature. The parts of mechanical devices used to shape the objects are stiff and hard, so these approaches are not suitable for soft samples. The top-down approach assumes that nanodevices must be produced piece by piece in a series of steps, much like manufactured goods are made. Scanning probe microscopy (SPM) is an important technique used both for the synthesis and characterization of nanomaterial by a top-down approach. Atomic force microscopy (AFM) tips can be used as a nanoscale "write head" to deposit a resist, which is then followed by an etching process to remove material in a top-down approach.
Some common techniques used in the top-down approach include:
a.) Mechanical milling: High-energy mechanical forces are applied to break down large particles into smaller ones, eventually reaching the nanoscale range.
b.) Lithography: Techniques like electron beam lithography or photolithography are used to create patterns on a substrate, defining the nanoscale features.
c.) Etching: Chemical or plasma etching is used to remove material from a larger sample, creating nanoscale structures.
d.) Nanolithography: Specialized lithography techniques are used to directly write or print nanoscale patterns on material.
Advantages of the Top-down Approaches:
1.) This Top-down approach is often suitable for large-scale production of nanomaterials, making it economically viable.
2.) Many top-down approaches have been widely used and optimized for bulk materials, which can be adapted for nanomaterial synthesis.
3.) This approach allows precise control over the size and shape of the resulting nanomaterials.
4.) Suitable for laboratory experimentation.
Disadvantages Top-down Approaches:
1.) It is required large installations and huge capital is required for building their setup.
2.) These approaches are quite expensive.
3.) The growth process is slow and hence these approaches are not suitable for large-scale production.
4.) The biggest problem in the approach is the imperfection of surface structure.
5.) The mechanical and chemical processes involved in the top-down approach can introduce defects in the nanomaterials, affecting their properties.
6.) This approach generates a significant amount of waste during the material reduction process, which can be environmentally problematic.
7.) As the approach starts with larger structures and reduces their size, it may be challenging to achieve precise control over nanoscale features, leading to variations in properties.
B.) Bottom-up Approaches: In this approach, It involves atom-by-atom, molecule-by-molecule, or cluster-by-cluster manipulation for the synthesis of nanostructures. It means that atoms are assembled into molecules, molecules are assembled into clusters, and the clusters are assembled to form the nanoparticle. This approach relies on self-assembly and controlled growth to create the desired nanoscale structure.
The bottom-up approach is based on the principle of molecular recognition (that is self-assembly). Self-assembly means growing more and more things of one's kind from themselves. The principle of self-assembly (shake and bake) involves assembling precursors in random positions and orientations, providing energy (shaking) to enable them to explore configuration space. The hugeness of this space suggests that a convergent pathway is inherent in the process in order to allow it to be completed in a reasonable time. Once the precursors are in position, "baking" may be required to strengthen the bonds connecting them and fix the final object permanently.
Some common techniques used in the bottom-up approach include:
a.) Chemical Synthesis: Chemical reactions are used to build up nanomaterials from atomic or molecular precursors, allowing precise control over the final product's size and shape.
b.) Self-Assembly: Molecules or nanoparticles are designed to interact in a way that leads to their spontaneous arrangement into specific nanoscale structures.
c.) Vapor Deposition: Nanoscale materials are grown layer by layer on a substrate by allowing precursor gases to react on its surface.
d.) Sol-Gel Process: Nanomaterials are formed by hydrolyzing metal alkoxides in a solution, followed by gelation and controlled drying.
The bottom-up approach allows for greater control over the nanomaterial's properties and can potentially lead to unique properties not found in their bulk counterparts. However, it can be more challenging to scale up these processes for mass production compared to the top-down approach.
Advantages of Bottom-down Approaches:
1.) The bottom-up approach allows for precise control at the atomic or molecular level, leading to well-defined nanomaterials with specific properties.
2.) Since the materials are assembled from individual atoms or molecules, there are fewer defects compared to the top-down approach.
3.) Bottom-up synthesis can result in unique nanomaterials with properties not easily achievable through top-down approaches.
Disadvantages of Bottom-down Approaches:
1.) Bottom-up approaches can be more complex and expensive, especially for large-scale production.
2.) Some bottom-up approaches may not be easily scalable for mass production, limiting their industrial applicability.
3.) Achieving high purity and reproducibility in bottom-up synthesis can be challenging due to the intricate processes involved.
Both the top-down and bottom-up approaches have their advantages and disadvantages, and researchers often choose the most suitable method based on the specific properties and applications of the nanomaterial they aim to create. Additionally, a combination of these approaches, known as "hybrid approaches," can be used to achieve even more complex nanoscale structures with tailored properties.
The synthesis of nanomaterial according to technique:
1.) Physical Methods
2.) Chemical Methods
3.) Biological Methods
1.) Physical Methods: Nanoparticles may be synthesized using a number of physical methods which are listed below. These methods are of two types viz mechanical type and vapor deposition type. These methods work at very high temperatures. The highest working temperatures are usually greater than $350^{\circ}C$.
- Arc Discharge Method
- Electron beam Lithography
- Mechanical Grinding
- Inert Gas condensation
- Ion Implantation
- Ball Milling
- Spray pyrolysis
- Vapour phase synthesis
2.) Chemical Methods: These are very simple methods for synthesizing nanoparticles and are very less expensive. The highest working temperatures are usually below $350^{\circ}C$. Large quantities of materials can be produced with a variety of sizes and shapes of particles. A number of chemical methods are shown below.
- Coprecipitation Method
- Microemulsion Method
- Electrochemical Method (Electrolysis)
- Chemical reduction of metal Salts Pyrolysis
- Phytochemical (irradiation Method)
- Solvothermal synthesis
- Sol-Gel process
- Sonochemical methods
3.) Biological Methods: Biological Methods are based on the use of microorganisms (Fungi, yeast, Bacteria, etc.) or plant extracts (and enzymes) or the use of templates such as DNA, viruses and membranes, etc. This type of synthesis is environmentally friendly and least toxic and therefore called green synthesis. Various green methods for the synthesis of nanoparticles are shown below.
- Using Plants and their extracts
- Using microorganisms (Bacteria, Fungi, and actinomycetes)
- Using algae
- Using enzymes and biomolecules
- Using industrial and agricultural wastes