Diamagnetic Substances and Its properties

Diamagnetic Substances :

Those substances, which are placed in the external magnetic field then they weakly magnetize in the opposite direction of the external magnetic field, are called diamagnetic substances. The susceptibility $\chi_{m} $ of diamagnetic substances is small and negative. Further, When diamagnetic substance placed in magnetic field then the flux density of the diamagnetic substance is slightly less than that in the free space. Thus, the relative permeability of diamagnetic substance $\mu_{r}$, is slightly less than 1.

Properties of Diamagnetic substances:

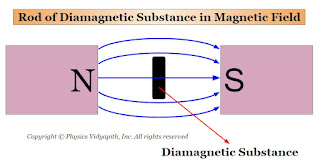
1. When a rod of a diamagnetic material is suspended freely between external magnetic poles (i.e. Between North and South Poles) then its axis becomes perpendicular to the external magnetic field $B$ (Figure). The poles produced on the two sides of the rod are similar to the poles of the external magnetic field.

2. In a non-uniform magnetic field, a diamagnetic substance tends to move from the stronger magnetic field to the weaker magnetic field. If a diamagnetic liquid is taken in a watch glass placed on two magnetic poles very near to each other, then the liquid is depressed in the middle as shown in figure below(Figure) where the field is strongest. Now, if the distance between the poles is increased, the liquid rises in the middle, because now the field is strongest near the poles.

3. If the solution of diamagnetic substance is poured into a U-tube and apply the strong magnetic field into one arm of this U-tube then the level of the solution in that arm is depressed. As shown in the figure below:

4. When diamagnetic gas molecules are passed between the poles of a magnet then diamagnetic gas molecules are spread across the field.

5. The susceptibility of a diamagnetic substance is independent of temperature.

Explanation of Diamagnetism on the Basis of Atomic Model:

The property of diamagnetism is generally found in those substances whose atoms (or ions or molecules) have an 'even' number of electrons. These even numbers of electron form pairs. In each pair of electrons, the spin of one electron is opposite to the other. So, the magnetic moment of one electron is opposite to the others because of that, the effect of magnetic dipole moments are neutralized by each other. As such, the net magnetic dipole moment of an atom (or ion or molecule) of a diamagnetic substance is zero.

When a diamagnetic substance is placed in an external magnetic field $B$ then this external magnetic field modifies the motion of the electrons in the atoms (or ions or molecules). Due to this, In each pair of electrons, the spin of one electron is become fast (Lenz's Law) and the other is slow due to that , the net magnetic dipole moment of the paired electron does not zero. Thus, a small magnetic dipole moment is induced in each atom of the substance (or ion or molecule) which is directly proportional to the magnetic field $B$ and opposite to its direction. Hence, the diamagnetic substance is magnetized opposite to the external magnetic field $B$, and the field lines become less dense inside the diamagnetic substance compared to those outside.

If the temperature of the diamagnetic substance is changed, there is no effect on its diamagnetic property. Thus, diamagnetism is temperature-independent.

Read More

Distinction between Spontaneous and Stimulated Emission of Radiation

Some of the differences between spontaneous and stimulated emission of radiation are given as follows:

1. In spontaneous emission, an atom in excited state falls to the ground state on its own without any incident photon while in stimulated emission transition takes place by stimulating photons or by an external agency.

2. In stimulated emission for each incident photon there are two outgoing photons in the same direction while in spontaneous emission the emitted photons move randomly in any direction.

3. The photons emitted in spontaneous emiss ion have a random phase and hence are incoherent while in stimulated emission the emitted photons are in phase and hence are coherent.

4. The rate of spontaneous emission is proportional to only the number of atoms in the excited state while the rate of stimulated emission is proportional to the number of atoms left in the excited state as well as on the energy density of the incident radiation.

5. In stimulated emission of radiation an amplified beam is achieved while in spontaneous emission there is no such amplification.

6. The light emitted through the spontaneous emission is not monochromatic while in stimulated transition monochromatic radiation is obtained.

7. Spontaneous emission is not controllable from outside while stimulated emission is controllable from outside.

8. In spontaneous emission, the net intensity is proportional to the number of radiating atoms while in stimulated emission it is proportional to the square of the number of radiation atoms.

Read More

Minimum Energy Or Zero Point Energy of a Particle in an one dimensional potential box or Infinite Well

Zero Point Energy of a Particle in an Infinite Well Potential Well:

The normalized wave function or eigenwave function:

$\psi_{n}(x) = \sqrt{\frac{2}{L}} sin \left( \frac{n\pi x}{L} \right)$

The probability density

$| \psi_{n}(x)|^{2} = \frac{2}{L} sin^{2} \left( \frac{n\pi x}{L} \right)$

The energy of a particle in a one-dimensional box or infinite potential well:

$E_{n}=\frac{n^{2}h^{2}}{8 mL^{2}}$

Where $n$ is called the quantum number and $n=1,2,3,4..........$ For $n=0, \psi_{n}(x)=0$ and $| \psi_{n}(x)|^{2}=0$. This shows that for $n=0$ $| \psi_{n}(x)|^{2}=0$ will be zero everywhere in the box which means that the probability of finding the particle inside the box is zero. i.e. particle is not present at all inside the box. Thus $n=0$ is not possible.

If $n\neq 0$ then $E \neq 0$. This means that the minimum energy of the particle in the box will not be zero. The minimum energy value will be obtained for the next lowest value of $n$ i.e. for $n=1$, which is

$E_{1}=\frac{h^{2}}{8 mL^{2}}$

This minimum energy of the particle is often called zero point energy which is finite inside the box. According to classical mechanics, the minimum value $E=0$ is also permissible.

Read More

Bohr's Theory of Hydrogen-Like Atoms

A hydrogen-like atom consists of a very small positively-charged nucleus and an electron revolving in a stable circular orbit around the nucleus.

The radius of electrons in stationary orbits:

Let the charge, mass, velocity of the electron and the radius of the orbit is respectively  $e$, $m$, and $v$  and $r$. The $+ze$ is the positive charge on the nucleus where $Z$ is the atomic number of the atom. As We know that when an electron revolves around the nucleus then the centripetal force on an electron is provided by the electrostatic force of attraction between the nucleus and an electron, we have

$\frac{mv^{2}}{r}=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(e)}{r^{2}}$

$mv^{2}=\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} \qquad(1)$

According to the first postulate of Bohr's model of the atom, the angular momentum of the electron is

$mvr=n \frac{h}{2 \pi} \qquad(2)$

Where $n \: (=1,2,3,.....)$ is quantum number.

Now squaring equation $(2)$ and dividing by equation $(1)$, we get

$r=n^{2} \frac{h^{2} \epsilon_{\circ}}{\pi m Z e^{2}} \qquad(3)$

The above equation is for the radii of the permitted orbits. From the above equation, this concluded that

$r \propto n^{2}$

Since, $n =1,2,3,.....$ it follows that the radii of the permitted orbits increased in the ratio $1:4:9:16:,.....$ from the first orbit.

Bohr's Radius:

For Hydrogen Atom $(z=1)$, The radius of the atom of the first orbit $(n=1)$ will be

$r_{1}= \frac{h^{2} \epsilon_{\circ}}{\pi m e^{2}}$

This is called Bohr's radius and its value is $0.53 A^{\circ}$. Since $r \propto n^{2}$, the radius of the second orbit of the hydrogen atom will be $( 4 \times 0.53 A^{\circ}) $ and that of the third orbit $9 \times 0.53 A^{\circ}$

The velocity of electrons in stationary orbits:

The velocity of the electron in permitted orbits can be obtained by the formula of equation $(2)$

$v=n\frac{h}{2 \pi m r}$

Now put the value of $r$ in above eqaution from equation $(3)$, we get

$v=\frac{Ze^{2}}{2 h \epsilon_{\circ}} \left( \frac{1}{n} \right) \quad(4)$

Thus $v \propto \frac{1}{n}$

This shows that the velocity of the electron is maximum in the lowest orbit $n=1$ and as goes on higher orbits velocity decreases.

For Hydrogen Atom $(z=1)$, The velocity of electron to move in the first orbit $(n=1)$ is

$v_{1}=\frac{e^{2}}{2h\epsilon_{\circ}}$

Its value is $2.19 \times 10^{6} m/sec$

Note:

$\frac{v_{1}}{c}= \frac{2.19 \times 10^{6}}{3 \times 10^{8}} =\frac{1}{137}$

Thus, $\frac{v_{1}}{c}$ or $\frac{e^{2}}{2h\epsilon_{\circ}}$ is a pure number. It is called the "Fine Structure Constant" and is denoted by $\alpha$

The energy of electrons in stationary orbits:

The total energy $E$ of a moving electron in an orbit is the sum of kinetic energies and potential energies. The kinetic energy of moving the electron in a stationary orbit is:

$K=\frac{1}{2} m v^{2}$

Now susbtitute the value of $v$ from equation $(1)$, we get

$K=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$

The potential energy of a moving electron in an orbit of radius $r$ due to the electrostatic attraction between nucleus and electron is given by

$U=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(-e)}{r}$

$U=-\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $

The total energy of the electron is

$E=K+U$

$E=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r} -\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $

$E=-\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$

Subtituting the value of $r$ in above equation from equation $(3)$, we get

$E=-\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n^{2}} \right) \qquad(5)$

This is the equation for the energy of the electron in the $n^{th}$ orbit.

Suppose, Excited state energy is $E_{2}$ and lower state energy is $E_{1}$. So the energy difference between these two states is:

$E_{2}- E_{1}= \frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}} \right) \qquad(6)$

According to the third postulate of Bohr's Atomic model, the frequency $\nu$ of the emitted electromagnetic wave:

$\nu=\frac{E_{2}- E_{1}}{h}$

$\nu=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$

The corresponding wavelength $\lambda$ of the emitted electromagnetic radiation is given by

$\frac{c}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$

$\frac{1}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(7)$

Where $\frac{1}{\lambda}$ is called "wave number" (i.e. number of waves per unit length). In the last equation$(7)$, the quantity $\frac{m e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}}$ is a constant an it is known as "Rydberg Constant (R)". That is

$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \qquad(8)$

So equation $(7)$ can be written as

$\frac{1}{\lambda}=z^{2} R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(9)$

This is Bohr's formula for hydrogen and hydrogen-like atoms $(He^{+}, Li^{++},.......)$.

For hydrogen $Z=1$

$\frac{1}{\lambda}= R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(10)$

The value of the Rydberg Constant is

$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} = 1.090 \times 10^{7} m^{-1}$

This value fairly agrees with empirical value $(1.097 \times 10^{7} m^{-1})$ obtained experimentally by Balmer.

The total energy in terms of Rydberg's Constant:

The $E$ expression can be written in terms of Rydberg's constant $R$ in a simplified form. So from equation $(5)$ and $(8)$ we get

$E=-Z^{2}\frac{Rhc}{n^{2}} \qquad(11)$

Putting the known values of $R$, $h$ and $c$ taking $1 eV =1.6 \times 10^{-19} \: J$ then we get

$E=-Z^{2}\frac{13.6}{n^{2}} \: eV \qquad(12)$

For a Hydrogen atom, $Z=1$

$E=-\frac{13.6}{n^{2}} \: eV \qquad(12)$

Read More

Bohr's Model of Atom

Bohr's Atomic Model Postulates:

Prof Neil in 1913 Bohr solve the difficulties of Ernest Rutherford's atomic model by applying Planck's quantum theory, For this, he proposed the following three Postulates:

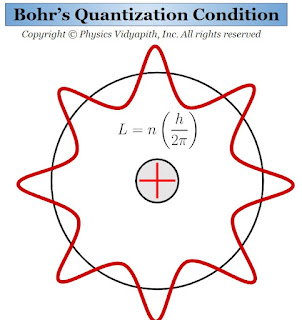
1.) Electrons can revolve only in those orbits in which their angular momentum is an integral multiple of $\frac{h}{2 \pi}$. These orbits have discrete energy and definite radii. So it is called the "stable orbits". If the mass of the electron is $m$ and it is revolving with velocity $v$ in an orbit of radius $r$, then its angular momentum will be $mvr$. According to Bohr's postulate,

$mvr=\frac{nh}{2\pi}$

Where $h$ is Planck's universal constant

This Bohr's equation is called the "Bohr's quantization Condition"

2.) When the electrons revolve in stable orbits then they do not radiate the energy in spite of their acceleration toward the center of the orbit. Hence atom remains stable and is said to exist in a stationary state.

3.) When the atoms receive energy from outside, then one (or more) of their outer electrons leaves their orbit and goes to some higher orbit. These states of the atoms are called the "excited states".

The electrons in the higher orbit stay only for $10^{-8} \: sec$ and return back to anyone lower orbit. While returning back of electrons to lower orbits, they radiate energy in the form of electromagnetic waves.

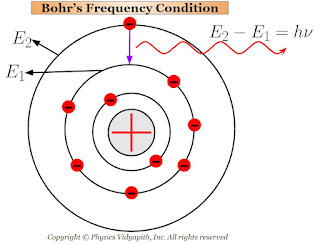
This radiated energy can be calculated by the energy difference of the electron between the two orbits (i.e. one is higher orbit and the other is lower orbit). If the energy of electron in the higher orbit is $E_{2}$ and that in the lower orbit is $E_{1}$ then net energy difference between the orbits:

$E=E_{2} - E_{1}$

$h \nu=E_{2} - E_{1} \qquad \left( \because E=h\nu \right)$

$\nu=\frac{E_{2} - E_{1}}{h}$

This Bohr's equation is called the "Bohr's frequency condition".

Read More