Bohr's Model of Atom

Bohr's Atomic Model Postulates:

Prof Neil in 1913 Bohr solve the difficulties of Ernest Rutherford's atomic model by applying Planck's quantum theory, For this, he proposed the following three Postulates:

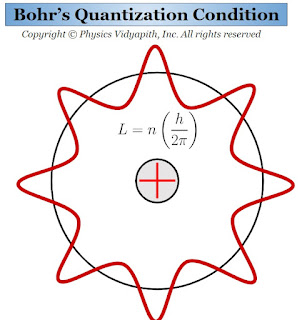
1.) Electrons can revolve only in those orbits in which their angular momentum is an integral multiple of $\frac{h}{2 \pi}$. These orbits have discrete energy and definite radii. So it is called the "stable orbits". If the mass of the electron is $m$ and it is revolving with velocity $v$ in an orbit of radius $r$, then its angular momentum will be $mvr$. According to Bohr's postulate,

$mvr=\frac{nh}{2\pi}$

Where $h$ is Planck's universal constant

This Bohr's equation is called the "Bohr's quantization Condition"

2.) When the electrons revolve in stable orbits then they do not radiate the energy in spite of their acceleration toward the center of the orbit. Hence atom remains stable and is said to exist in a stationary state.

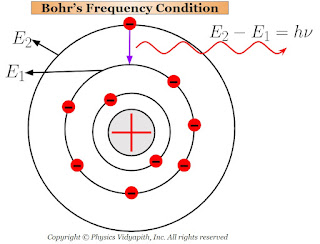
3.) When the atoms receive energy from outside, then one (or more) of their outer electrons leaves their orbit and goes to some higher orbit. These states of the atoms are called the "excited states".

The electrons in the higher orbit stay only for $10^{-8} \: sec$ and return back to anyone lower orbit. While returning back of electrons to lower orbits, they radiate energy in the form of electromagnetic waves.

This radiated energy can be calculated by the energy difference of the electron between the two orbits (i.e. one is higher orbit and the other is lower orbit). If the energy of electron in the higher orbit is $E_{2}$ and that in the lower orbit is $E_{1}$ then net energy difference between the orbits:

$E=E_{2} - E_{1}$

$h \nu=E_{2} - E_{1} \qquad \left( \because E=h\nu \right)$

$\nu=\frac{E_{2} - E_{1}}{h}$

This Bohr's equation is called the "Bohr's frequency condition".

Read More

Bohr's Quantization Condition

The Quantization Condition in Bohr Theory of Hydrogen Atom:

$L=\frac{nh}{2 \pi}$

For the angular momentum L, the electron moves arbitrarily only in a stationary circular orbit. According to De Broglie's hypothesis, this condition can be easily obtained. For this purpose, there are following assumptions given below:

1.) The motion of the electron in a stationary circular orbit is represented by a standing matter-wave. If the wavelength of the wave is $\lambda$ then the De Broglie relation

$\lambda=\frac{h}{mv} \qquad(1)$

Where
$m \rightarrow$ The mass of the electron and
$v \rightarrow$ The Velocity in the orbit.

2.) The circular orbit contains an integral number of wavelengths, i.e.

$2 \pi r_{n}= n \lambda $

$\frac{2 \pi r_{n}}{\lambda}= n \qquad(2)$

Where $n=1,2,3............$ and $r_{n}$ is the radius of the orbit.

Substituting the value of $\lambda$ in equation$(2)$

$\frac{2 \pi r_{n} m v}{h} =n$

$mvr_{n} =\frac{nh}{2\pi}$

$L=\frac{nh}{2\pi}$

Which is Bohr's quantization condition.

Read More

Drawbacks of Old Quantum Theory

Planck's quantum hypothesis with its application and extension to explain the black body radiation like the photo-electric effect, the Compton effect, the variation of specific heat of solid with temperature and the spectrum of hydrogen is now called the Old quantum theory. Through these phenomena are successfully explained by the theory, there are numerous drawbacks of the theory. A few of them are as follows.

1.) Bohr's quantization rules are arbitrary. The theory does not provide a physical explanation for the assumptions.

2.) The old quantum theory cannot be applied to explain the spectra of helium and of more complex atoms.

3.) It can provide only a qualitative and incomplete explanation of the intensities of the spectral lines.

4.) It can not explain the dispersion of light.

5.) The theory of non-harmonic vibrations of systems cannot be applied to explain the vibrations of systems.

Read More

One dimensional Step Potential Barrier for a Particle

Potential Step:

1.) In region $(I)$  i.e.$(-\infty \leq \: x \lt \: 0)$
2.) In region $(II)$ i.e. $(0 \leq \:x \: \leq +\infty)$
Case $(1)$	When $E \lt V_{\circ}$
A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$ B.) Expression for the wave function in the region $(I)$ and $(II)$ C.) Expression for the Probability Current Densities D.) Reflection and Transmission Coefficients
Case $(2)$ :	When $E \gt V_{\circ}$
A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$ B.) Expression for the wave function in the region $(I)$ and $(II)$ C.) Expression for the Probability Current Densities D.) Reflection and Transmission Coefficients

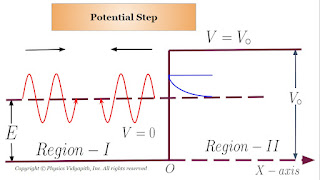
One dimensional step potential barrier for a particle is shown in the figure below.

The meaning of the figure is that the region $(I)$ is at left hand side of the origin $O$ and the potential energy of a particle is zero in this region $(I)$. The region $(II)$ is at the right hand side of $O$ and this region $II$ has constant potential equal to $V_{\circ}$. Such a potential barrier does not exist in nature, but it is approximately similar to the instantaneous potential difference between the dees of a cyclotron or the surface potential barrier of a metal.

Suppose a uniform beam of particles each of mass $m$ and having kinetic energy $E$ is traveling parallel to the x-axis from left to right in the region $(I)$, and is incident on the potential step. In region $(I)$ the energy $E$ of a particle is whole kinetic energy, and in region $(II)$ it is partly kinetic and partly potential energy.

If $E \lt V_{\circ}$, then according to classical mechanics, a particle can enter in the region $(II)$. However according to quantum mechanics although the wave function for an incident particle has a finite value in the region $(II)$ there is no steady transmission of the particle has finite value in this region $(II)$, all the particles are reflected back from the potential step $V_{\circ} \gt E$. In the following discussion, we investigate this behavior of the particles.

Let $\psi_{1}(x)$ and $\psi_{2}(x)$ be the wave function for the motion of a particle in the beam in the region $(I)$ and $(II)$ respectively.

1.) In region $(I)$ i.e. $(-\infty \leq \: x \lt \: 0)$:

According to the time-independent Schrodinger wave equation is:

$-\frac{\hbar^{2}}{2m} \frac{d^{2} \psi_{1}}{dx^{2}}=E \psi_{1}$

$\frac{d^{2} \psi_{1}}{dx^{2}} + \frac{2mE}{\hbar^{2}} \psi_{1} =0$

Let $k_{1}^{2}=\frac{2mE}{\hbar^{2}} $, Now substitute this value in the above equation that can be written as

$\frac{d^{2} \psi_{1}}{dx^{2}} + k_{1}^{2} \psi_{1} =0 \qquad(1)$

2.) In region $(II)$ i.e. $(0 \leq \:x \: \leq +\infty)$:

Case $(1)$ : When $E \lt V_{\circ}$

Then according to the time-independent Schrodinger wave equation for the above case is:

$\frac{d^{2} \psi_{2}}{dx^{2}} + \frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}} \psi_{2} =0$

$\frac{d^{2} \psi_{2}}{dx^{2}} - \frac{2m \left(V_{\circ} -E \right)}{\hbar^{2}} \psi_{2} =0$

Let $\beta^{2}=\frac{2m\left(V_{\circ} -E \right)}{\hbar^{2}} $, Now substitute this value in the above equation that can be written as

$\frac{d^{2} \psi_{2}}{dx^{2}} - \beta^{2} \psi_{2} =0 \qquad(2)$

The general solution of the equation $(1)$ and equation $(2)$ is

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad(3)$

$\psi_{2} (x) = C e^{- \beta \: x} + D e^{\beta \: x} \qquad(4)$

In equation $(3)$ the term $A e^{ik_{1}x}$ represents a wave of amplitude $A$ traveling in the positive x-axis direction and term $B e^{-ik_{1}x} $ is the wave of amplitude $B$ reflected from potential step in the negative x-axis direction. In equation $(4)$ the term $C e^{- \beta \: x}$ is an exponentially decreasing wave function representing a non-oscillatory disturbance that penetrates the potential barrier for some finite distance in the positive x-axis direction and the term $D e^{\beta \: x}$ is an exponentially increasing wave function in the positive x-axis direction. According to the physical interpretation, wave function $\psi$ must remain finite when $x$ approaches $\infty$. From this condition, it follows that $D=0$. Hence in the region $(II)$, the valid solution of the wave equation is:

$\psi_{2} (x) = C e^{- \beta \: x} \qquad(5)$

A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$:

i) At $x=0$, we have

$\psi_{1}(0) = \psi_{2}(0)$

So from equation $(3)$ and equation $(5)$, we have

$A+B=C \qquad(6)$

ii) We also have

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0} = \left( \frac{d\psi_{2}}{dx} \right)_{x=0}$

So again from equation $(3)$ and equation $(5)$, we have

$A\:i\:k_{1} - B\:i\:k_{1} = - C \: \beta$

$A - B = - \frac{C \: \beta}{i\:k_{1} }$

$A - B = \frac{iC \: \beta}{k_{1} } \qquad(7)$

Adding equation $(6)$ and equation $(7)$

$2A = \left( 1 + \frac{ i \beta}{k_{1}} \right)C$

$2A = \left(\frac{k_{1} + i \beta}{k_{1}} \right)C$

$C = \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A \qquad(8)$

Now subtracting the equation $(7)$ from equation $(6)$

$2B = \left( 1 - \frac{ i \beta}{k_{1}} \right)C$

$2B = \left(\frac{k_{1} - i \beta}{k_{1}} \right)C$

Now substitute the value of $C$ from equation $(8)$ in the above equation then we get

$2B = \left(\frac{k_{1} - i \beta}{k_{1}} \right) \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A$

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad(9)$

The equation $(8)$ and equation $(9)$ can be expressed in polar form.

Let $k_{1}= r \: cos\delta$ and $\beta=r\: sin \delta$

Then $r=\sqrt {k_{1}^{2} + \beta^{2}}$ and $tan \delta =\frac{\beta}{k_{1}}$

Now subtitute the value of $k_{1}$ and $\beta$ in equation $(9)$

Now substitute the value of $k_{1}$ and $\beta$ in equation $(9)$

$B = \left(\frac{r \: cos\delta - i r\: sin \delta}{r \: cos\delta + i r\: sin \delta} \right)A $

$B = \left(\frac{ \: cos\delta - i \: sin \delta}{ \: cos\delta + i \: sin \delta} \right)A $

$B = \left(\frac{ e^{-i\delta}}{ e^{i\delta}} \right)A $

$B = e^{-2i \delta} A \qquad(10) $

Now from eqaution $(8)$

$C = \left(\frac{2k_{1} }{k_{1} + i \beta} - 1 + 1 \right)A $

$C = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} +1 \right)A $

Now substitute the value of $k_{1}$ and $\beta$ in equation $(8)$

$C = \left(\frac{r \: cos\delta - i r\: sin \delta}{r \: cos\delta + i r\: sin \delta} +1 \right)A $

$C = \left(\frac{ \: cos\delta - i \: sin \delta}{ \: cos\delta + i \: sin \delta} +1 \right)A $

$C = \left(e^{-2i \delta} +1 \right)A \qquad(11)$

B.) Expression for the wave function in the region $(I)$ and $(II)$:

(i.) In region $(I)$: $x \lt 0$:

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$

Now substitute the value of $B$ in the above equation:

$\psi_{1} (x) = A e^{ik_{1}x} + e^{-2i \delta} A e^{-ik_{1}x} $

$\psi_{1} (x) = A e^{-i \delta} \left( e^{ik_{1}x} e^{i \delta} + e^{-i \delta} A e^{-ik_{1}x} \right) $

$\psi_{1} (x) = 2A e^{-i \delta} \left[ \frac{e^{ik_{1}x} e^{i \delta} + e^{-i \delta} A e^{-ik_{1}x}}{2} \right] $

$\psi_{1} (x) = 2A e^{-i \delta} cos \left(k_{1}x + \delta \right) \qquad(12) $

(ii.) In region $(II)$: $x \gt 0$:

$\psi_{2} (x) = C e^{- \beta \: x} \qquad \left\{ from \: eqaution \: (5) \right\}$

Now substitute the value of $C$ in the above equation:

$\psi_{2} (x) = \left(e^{-2i \delta} +1 \right)A e^{- \beta \: x} $

$\psi_{2} (x) = A e^{-i \delta} \left(e^{-i \delta} +e^{i \delta} \right) e^{- \beta \: x} $

$\psi_{2} (x) = 2A e^{-i \delta} \left( \frac{e^{-i \delta} +e^{i \delta}}{2} \right) e^{- \beta \: x} $

$\psi_{2} (x) = 2A e^{-i \delta} \left( \frac{e^{-i \delta} +e^{i \delta}}{2} \right) e^{- \beta \: x} $

$\psi_{2} (x) = \left( 2A e^{-i \delta} cos \delta \right) e^{- \beta \: x} \qquad(13)$

This shows that the wave function in the region $(II)$ is exponentially damped.

C.) Expression for the Probability Current Densities:

(i.) In region $(I)$:

a.) The probabilty current density $S_{1}$ for the incident beam of particle is given by

$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{i} =(A e^{ik_{1}x})(A e^{ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} e^{ik_{1}x} e^{-ik_{1}x} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} \frac{\hbar k_{1}}{m}$

$S_{i} = | A|^{2} \frac{\hbar k_{1}}{m} \qquad(14)$

b.) The probability current density $S_{r}$ for the reflected beam of particles is given by:

$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{r} =(B e^{-ik_{1}x})(B e^{-ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{r} = | B |^{2} \frac{\hbar k_{1}}{m} \qquad(15)$

Hence the net probability current density in the region $(I)$ is given by

$S=S_{i} - S_{r}$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - | B |^{2} \right) \qquad(16)$

The intensity of waves:

We know that

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad \left\{ From \: equation \: (9) \right\}$

The complex conjugate of this equation is:

$B^{*} = \left(\frac{k_{1} + i \beta}{k_{1} - i \beta} \right)A^{*} $

$BB^{*}=AA^{*}$

$ | B^{2} | = | A^{2}| \qquad(17)$

Hence the net probability current in the region $(I)$ to the left of the region $O$ is zero.

The equation $ | B^{2} | = | A^{2}|$ shows that the intensity of the reflected wave is equal to that of the incident wave, or the number of particles per second passing normally through the unit area of the incident beam is equal to the number of particles per second passing normally through unit area of the reflected beam. Consequently, the incident and reflected probability currents cancel one another.

(ii.) In region $(II)$:

From the relation $ | B^{2} | = | A^{2}|$ we infer that the probability current density in the region $(II)$ to the right of the origin should be zero. However, we can prove this conclusion using the wave function

$\psi_{2}= C e^{-\beta x}$

and its complex conjugate

$\psi^{*}_{2}= C^{*} e^{-\beta x}$

The proof is as follows:

The probability current density in the region $(II)$ for the transmitted beam of the particles is given by

$S_{t}= -\frac{i \hbar}{2m} \left[ \psi^{*}_{2} \frac{\partial \psi_{2}}{\partial x} - \psi_{2} \frac{\partial \psi^{*}_{2}}{\partial x} \right]$

Now Substitute the value of $\psi$ and $\psi^{*}$ in this above equation:

$S_{t}= -\frac{i \hbar}{2m} \left[C^{*} e^{-\beta x} \frac{\partial C e^{-\beta x}}{\partial x} - C e^{-\beta x} \frac{\partial C^{*} e^{-\beta x}}{\partial x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} - CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} - CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[-CC^{*} e^{-2\beta x} (\beta) + CC^{*} e^{-2\beta x} (\beta) \right]$

$S_{t}=0 \qquad(18)$

The probability current density $S_{t}$ for a transmitted beam of particles is zero

D.) Reflection and Transmission Coefficients:

(i.)Reflection Coefficients:

The reflection coefficient $R$ is defined as the ratio of the probability current density $S_{r}$ for the reflected beam of particles to the probability current density $S_{i}$ for the incident beam of particles. Thus it is given by

$R=\frac{S_{r}}{S_{i}}$

$R=\frac{| B |^{2} \frac{\hbar k_{1}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$R=\frac{| B |^{2} }{| A |^{2}} \qquad(19)$

In this case $(V_{\circ} \gt E)$, $ | B^{2} | = | A^{2}|$ Now the above equation $(19)$ can be written as

$R=1 \qquad(20)$

This shows that the reflection of the incident beam, at the potential step is total.

(ii) Transmission Coefficients:

The transmission coefficient $T$ is defined as the ratio of the probability current density $S_{t}$ for the transmitted beam of the particle to the probability current density $S_{i}$ for the incident beam. Thus it is given by

$T=\frac{S_{t}}{S_{i}} \qquad(21)$

In this case: The probability of current densityin region $(II)$ is zero i.e. $S_{t}=0$ then transmission coefficient

$T=0$

So from above equation, we can conclude that the transmission coefficient of the beam of particles is zero.

Conclusions:

From the foregoing discussion, we draw the following inference:

i.) The reflection of the incident beam of particles, at the potential step is total.

ii.) There is no probability of current density anywhere. To the left hand side of the potential step, the incident and the reflected probability of currents density cancel to each other, and to the right ahnd side of the step, probability of currents density is zero.

iii.) To the right of the step the wave function is not zero, but it is exponentially damped. Therefore there is a finite or definite probability of finding the particle in the region $(II)$

If $V_{\circ} \rightarrow \infty$ and $E$ is finite, then

$\beta=\sqrt {\frac{2m \left( V_{\circ} -E \right)}{\hbar^{2}}} \rightarrow \infty $

In this case the wave function in region $(II)$ is $\psi_{2}= C \: e^{-\beta x} \rightarrow 0 $

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A $, and $C = \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A$

$\underset{\beta \rightarrow \infty}{Lim} \:\: \frac{B}{A}=\frac{\frac{k_{1}}{\beta} - i}{\frac{k_{1}}{\beta}+i} = -1$

$\frac{B}{A} =-1$ Or $A+B=0$ $\qquad(22)$

And, $\underset{\beta \rightarrow \infty}{Lim} \:\: \frac{C}{A}=\frac{2k_{1}} {k_{1}+i \beta} = 0$

$C=0 \qquad(23)$

Or

Hence the wave function

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ From \: equation (3) \right\}$

At $x=0$ is

$\psi_{1} (0) = A + B=0 \qquad(24)$

And the wave function $\psi_{2}= C \: e^{-\beta x}$

At $x=0$ is $\psi_{2}=C=0$

The slope of $\psi_{1}$ at $x=0$ is

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0}= ik_{1} \left( A-B \right) = 2 i k_{1} A \qquad(25)$

Thus at a point where the potential suddenly increases from zero to an infinite value the wave function $\psi_{1}$ becomes zero and ts slope suddenly falls from a finite value $2ik_{1}A$ to zero.

In region $(II)$ : $(0 \leq \:x \: \leq +\infty)$:

Case $(2)$ : When $E \gt V_{\circ}$

If $E \gt V_{\circ}$, then the time-independent Schrodinger wave equation is

$\frac{d^{2} \psi_{2}}{dx^{2}} + \frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}} \psi_{2} =0$

Let $k_{2}^{2}=\frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}}$, Now put this value in the above equation which can be written as

$\frac{d^{2} \psi_{2}}{dx^{2}} - k_{2}^{2} \psi_{2} =0 \qquad(26)$

The general solution of the equation $(26)$ is

$\psi_{2} (x) = G e^{ik_{2}x} + H e^{-ik_{1}x} \qquad(27)$

In this equation the term $G e^{ik_{2}x}$ represents a wave traveling from the potential step in the positive x-direction, and the term $H e^{-ik_{1}x}$ a wave traveling in the negative x-direction towards the potential step. Since the particles are incident only from the left of the potential step $H$ must be zero. Hence in the region, $(II)$ the valid solution of the wave equation is

$\psi_{2} (x) = G e^{ik_{2}x} \qquad(28)$

A.) Expression for the Amplitudes $B$ and $G$ in terms of the Amplitude $A$:

i) At $x=0$, we have

$\psi_{1}(0) = \psi_{2}(0)$

So from equation $(3)$ and equation $(28)$, we have

$A+B=G \qquad(29)$

ii) At this condition that the derivative of the wave function is continuous at $x=0$

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0} = \left( \frac{d\psi_{2}}{dx} \right)_{x=0}$

$A \: ik_{1} - B \: ik_{1} =G \: ik_{2} $

$A-B =\frac{k_{2}}{k_{1}}G \qquad(30)$

Adding equation $(29)$ and equation $(30)$, we get

$2A=\left(\frac{k_{1}+k_{2}}{k_{1}}\right) G$

$G=\left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A \qquad(31)$

Subtracting equation $(30)$ and equation $(29)$, we get

$2B=\left(\frac{k_{1} - k_{2}}{k_{1}}\right) G$

Now subtitute the vaue of $G$ from equation $(31)$ to the above equation

$2B=\left(\frac{k_{1} - k_{2}}{k_{1}}\right) \left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A$

$B=\left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right) A \qquad(32)$

B.) Expression for the wave function in region $(I)$ and $(II)$

(i.) In region $(I)$: $x \lt 0$:

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$

$\psi_{1} = A \left[ e^{ik_{1}x} + \left( \frac{k_{1} - k_{2}}{k_{1} +k_{2}} \right) e^{-ik_{1}x} \right] \qquad(33)$

ii.) In region $(II)$: $x \gt 0$:

$\psi_{2} (x) = G e^{ i k_{2} \: x} \qquad \left\{ from \: eqaution \: (28) \right\}$

$\psi_{2} (x) = \left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A e^{ i k_{2} \: x} \qquad (34)$

C.) Expression for the Probability Current Densities:

(i.) In region $(I)$:

a.) The probabilty current density $S_{1}$ for the incident beam of particle is given by

$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{i} =(A e^{ik_{1}x})(A e^{ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} e^{ik_{1}x} e^{-ik_{1}x} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} \frac{\hbar k_{1}}{m}$

$S_{i} = | A |^{2} \frac{\hbar k_{1}}{m} \qquad(35)$

b.) The probability current density $S_{r}$ for the reflected beam of particles is given by:

$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{r} =(B e^{-ik_{1}x})(B e^{-ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{r} = | B |^{2} \frac{\hbar k_{1}}{m} \qquad(36)$

Hence the net probability current density in the region $(I)$ is given by

$S=S_{i} - S_{r}$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - | B |^{2} \right) \qquad(37)$

From equation $(32)$

$|B|^{2}=\left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

Substitute the above equation value in equation $(37)$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - \left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} |A|^{2} \right)$

$S=\frac{\hbar k_{1}}{m} | A |^{2} \left[ 1 - \left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} \right]$

$S=\frac{\hbar k_{1}}{m} |A|^{2} \left[ \frac{4 k_{1} k_{2}}{\left(k_{1} +k_{2} \right)^{2}} \right]$

$S=\frac{4 k_{1} k_{2}}{\left(k_{1} +k_{2}\right)^{2}} \left( \frac{\hbar k_{1}}{m} \right) | A |^{2} \qquad(38)$

(ii.) In region $(II)$:

The probability current density $S_{t}$ for the transmitted beam of particles in region $(II)$ is given by

$S_{t}= \left( G e^{ i k_{2} \: x} \right) \left( G e^{ i k_{2} \: x} \right)^{*} \frac{\hbar k_{2}}{m} $

$S_{t}= \frac{\hbar k_{2}}{m} |G|^{2} \qquad(39)$

From equation $(31)$, we have

$|G|^{2}=\left(\frac{2k_{1}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

So substitute the value of the above equation in equation $(39)$, then we get

$S_{t}= \frac{\hbar k_{2}}{m} \left(\frac{2k_{1}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

$S_{t}= \frac{4k^{2}_{1}}{\left(k_{1} +k_{2}\right)^{2}} \left( \frac{\hbar k_{2}}{m} \right) |A|^{2} \qquad(40)$

The equation $(38)$ and equation $(40)$ shows that $S=S_{t}$. i.e. The net probability density in the direction from left to right in the region $(I)$ is equal to the probability current density in the region $(II)$.

D.) Reflection and Transmission Coefficients:

(i.)Reflection Coefficients:

The reflection coefficient $R$ is defined as the ratio of the probability current density $S_{r}$ for the reflected beam of particles to the probability current density $S_{i}$ for the incident beam of particles. Thus it is given by

$R=\frac{S_{r}}{S_{i}}$

$R=\frac{| B |^{2} \frac{\hbar k_{1}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$R=\frac{| B |^{2} }{| A |^{2}}$

Now using the equation $(32)$ we get

$R=\frac{\left( k_{1} -k_{2} \right)}{\left( k_{1} + k_{2} \right)} \qquad(41)$

(ii) Transmission Coefficients:

The transmission coefficient $T$ is defined as the ratio of the probability current density $S_{t}$ for the transmitted beam of the particle to the probability current density $S_{i}$ for the incident beam. Thus it is given by

$T=\frac{S_{t}}{S_{i}} $

$T=\frac{| G |^{2} \frac{\hbar k_{2}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$T=\frac{| G |^{2} k_{2}}{ | A |^{2} k_{1} }$

Now using equation $(31)$, we get

$T= \frac{k_{2}}{k_{1}} \left( \frac{2 k_{1}}{k_{1} + k_{2}} \right)^{2}$

$T= \frac{k_{2}}{k_{1}} \frac{4 k^{2}_{1}}{\left( k_{1} + k_{2} \right)^{2}} \qquad(42)$

Adding the equation $(41)$ and equation $(42)$ it is easily verified that

$R+T=1 \qquad(43)$

Read More

Wave function of a particle in free state

The wave function of a free particle:

Suppose a particle of mass $m$ is in motion along the x-axis. Suppose no force is acting on the particle so that the potential energy of the particle is constant. For convenience, the constant potential energy is taken to b zero. Hence, the time-independent Schrodinger equation for a free particle is given by:

$-\frac{\hbar^{2}}{2m} \frac{d^{2} \psi}{dx^{2}}=E \psi \qquad(1)$

Since the particle is moving freely with zero potential energy, its total energy $E$ is the kinetic energy given by

$E=\frac{p^{2}_{x}}{2m}$

Where $p_{x}$ is the momentum of the particle that is moving along the x-axis.

$\frac{d^{2} \psi}{dx^{2}} + \frac{2mE}{\hbar^{2}} \psi =0 \qquad(2)$

Let $k^{2}=\frac{2mE}{\hbar^{2}} $,

Now substitute the value of $k^{2}$ in the above equation $(2)$ that can be written as

$\frac{d^{2} \psi}{dx^{2}} + k^{2} \psi =0 \qquad(3)$

The solution of the above equation $(3)$

$\psi (x) = A e^{ikx} + B e^{-ikx} \qquad(4)$

Here $A$ and $B$ are constants.

The equation$(4)$ gives the wave function of time independent. The complete wave function (i.e for both time-dependent and independent ) for a particle is given by

$\psi(x,t)=\psi(x) e^{-i\omega t}$

$\psi(x,t)=\left( A e^{ikx} + B e^{-ikx} \right) e^{-i\omega t}$

$\psi(x,t)=A e^{\left(ikx-i\omega t \right)} + B e^{\left(-ikx -i\omega t \right)} $

$\psi(x,t)= A e^{-i\left(\omega t - kx \right)} + B e^{-i\left(\omega t + kx\right)} \quad(5)$

The above equation $(5)$ represents a continuous plane simple harmonic wave. The first term on the right side of the above equation $(5)$ represents the wave traveling in the positive x-direction, and the second term represents the wave traveling in the negative x-direction. Therefore, the wave function for the motion of a particle in the positive x-direction, we have

$\psi(x,t)= A e^{-i\left(\omega t - kx \right)} \qquad(6)$

The complex conjugate of the above wave function equation of free particle:

$\psi^{*}(x,t)= A e^{i\left(\omega t - k x \right)} \quad(7)$

Eigenfunction and Eigen Value of linear momentum operator:

Now the momentum operator $\frac{\hbar}{i} \frac{\partial}{\partial x}$, operating on the equation $(6)$ i.e wave function of a free particle moving along the positive x-axis:

$\frac{\hbar}{i} \frac{\partial \psi(x,t)}{\partial x}= \frac{\hbar}{i} \frac{\partial }{\partial x} \left[ A e^{-i\left(\omega t - k x \right)} \right]$

$\frac{\hbar}{i} \frac{\partial \psi(x,t)}{\partial x}= \frac{\hbar}{i} \left[ A \left( ik \right)e^{-i\left(\omega t - kx \right)} \right]$

$\frac{\hbar}{i} \frac{\partial \psi(x,t)}{\partial x}= \hbar k \left[ A e^{-i\left(\omega t - kx \right)} \right]$

$\frac{\hbar}{i} \frac{\partial \psi(x,t)}{\partial x}= \hbar k \psi(x,t) \qquad(8)$

This equation shows that the wave function $\psi(x,t)$ for the particle is an eigenfunction of the linear momentum operator, and the momentum $p_{x}$ is the eigenvalue of the operator. Hence the momentum remains sharp with the value $p_{x}$

Probability of finding the free particle:

The probability of finding the position a particle in the region between $x$ and $x+dx$ is given by

$P \: dx =\psi(x,t) \psi^{*}(x,t) dx \qquad(8)$

Now substitute the value of $\psi(x,t)$ and $\psi^{*}(x,t)$ from equation $(6)$ and equation $(7)$ in above equation $(8)$, then we get

$P \: dx = A^{2} dx \qquad(9)$

Therefore the probability density $P$ for the position of the particle with the definite value of momentum is constant over the x-axis, i.e., All positions of the particle are equally probable. This conclusion is also obtained from the principle of uncertainty.

According to the interpretation of the wave function, the probability of finding the particle somewhere in space must be equal to $1$. i.e

$\int_{-\infty}^{+\infty} \psi(x,t) \psi^{*}(x,t) dx=1 \qquad(9)$

In this case $\psi(x,t) \psi^{*}(x,t) = A^{2}$ ,

There, the integral on the left side of the equation $(9)$ is infinite. Hence the wave function for the free particle cannot be normalized and $A$ must remain arbitrary. The difficulty arises because we are dealing with an ideal case. In practice, we can not have an absolutely free particle. The particle will always be confined within an enclosure in the laboratory, and hence its position can be determined. This means that its momentum cannot be determined with absolute accuracy.

Read More