A.) Combination of cells when emf of cells are same:
There are three types of combinations of cells in the circuit
1.) Series Combination of Cells
2.) Parallel Combination of Cells
3.) Mixed Combination of Cells
1.) Series Combination of Cells: Let us consider that the $n$ - cells having emf (electromotive force) $E$ and internal resistance $r$ are connected in series with external resistance $R$. Then from the figure given below
The total emf of the $n$ - cell = $nE$
The total internal resistance of the $n$ - cell = $nr$
The total resistance of the circuit = $nr+R$
The total current in the circuit
$i=\frac{Total \: emf \: of \: the \: n - series \: cell}{Total \: resistance \: of \: the \: circuit}$
$i=\frac{nE}{nr+R}$
2.) Parallel Combination of Cells: Let us consider that the $n$ - cells having emf (electromotive force) $E$ and internal resistance $r$ are connected in parallel with external resistance $R$. Then from the figure given below
The total emf of the $n$ - cell = $E$
The total internal resistance of the $n$ - cell
$\frac{1}{r_{eq}} = \frac{1}{r}+ \frac{1}{r}+.........n \: times$
$\frac{1}{r_{eq}}=\frac{n}{r}$
$r_{eq}=\frac{r}{n}$
The total resistance of the circuit = $\frac{r}{n}+R$
The total current in the circuit
$i=\frac{Total \: emf \: of \: the \: n - parallel \: cell}{Total \: resistance \: of \: the \: circuit}$
$i=\frac{E}{\frac{r}{n}+R}$
$i=\frac{E}{\frac{r+nR}{n}}$
$i=\frac{nE}{r+nR}$
3.) Mixed Combination of Cells: Let us consider that the $n$ - cells having emf (electromotive force) $E$ and internal resistance $r$ are connected in series in each row of $m$ parallel rows with external resistance $R$. Then from the figure given below
The total emf of the $n$ - cell in each row of $m$ parallel rows of the cells = $nE$
The internal resistance of the $n$ - cell in each row = $nr$
The total internal resistance of the $n$ - cell in each of $m$ parallel rows of the cells = $nr$
$\frac{1}{r_{eq}} = \frac{1}{nr}+ \frac{1}{nr}+.........m \: times$
$\frac{1}{r_{eq}}=\frac{m}{nr}$
$r_{eq}=\frac{nr}{m}$
The total resistance of the circuit = $\frac{nr}{m}+R$
The total current in the circuit
$i=\frac{Total \: emf \: of \: the \: cell}{Total \: resistance \: of \: the \: circuit}$
$i=\frac{nE}{\frac{nr}{m}+R}$
$i=\frac{nE}{\frac{nr+mR}{m}}$
$i=\frac{mnE}{nr+mR}$
It is clear from the above equation that for the value of $i$ to be maximum, the value of $(nr+mR)$ should be minimum. Now,
$nr+mR= \left[ \sqrt{nr}-\sqrt{mr} \right]^{2}+2 \sqrt{mnRr}$
Therefore, for $(nr+mR)$ to be minimum, the quantity $\left[ \sqrt{nr}-\sqrt{mr} \right]^{2}$ should be minimum. So
$\left[ \sqrt{nr}-\sqrt{mr} \right]^{2} = 0$
$ \sqrt{nr}-\sqrt{mr} = 0$
$ \sqrt{nr} = \sqrt{mr} $
$nr=mR$
$R=\frac{nr}{m}$
Here, $\frac{nr}{m}$ is the total resistance of the cells.
Thus, When the total internal resistance of the cells are equal to the external resistance then the total current in the external circuit will be maximum in the mixed combination of cells.
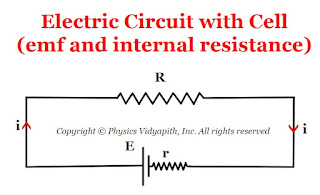
Relation between electromotive force (E), internal resistance (r) and potential difference (V) in a circuit
Relation between electromotive force $(E)$, internal resistance $(r)$ and potential difference $(V)$:
Let us consider:
The cell having electro-motive force = $E$
The cell having internal resistance = $r$
The external resistance of the circuit = $R$
The potential difference between the external resistance of the circuit = $V$
The current in circuit = $i$
So, The emf of the cell from the given circuit in the figure above
$E=iR+ir$
$E = V+ir$
$V=E-ir$
Resolving Power of Optical Instrument | Rayleigh Criterion of Resolution
Resolving power of an optical instrument:
The ability of an optical instrument to just resolve the images of two closely spaced objects is called its resolving power.
Limit of Resolution:
The smallest distance between two closely spaced objects that can be seen as separated or just separated from each other through an optical instrument is known as the limit of resolution of that optical instrument.
Rayleigh Criterion:
Rayleigh criterion describes the separation between the two objects or wavelengths (i.e. resolving power) by the resultant intensity distribution of objects and wavelengths. According to Rayleigh's criterion, there are the following cases:
Case:1 If two point sources have very small angular separation, then central or principal maxima in their diffraction patterns will overlap to a large extent and resultant intensity shows uniform variation. As shown in the figure below. In this case, the two objects or wavelengths can not be distinguished or unresolved.
Case:2 If two point sources have very large angular separation then the central or principal maxima are widely separated and the resultant intensity shows two widely separated peaks. As shown in the figure below. In this case, the objects or wavelengths are resolved well.
Case:3 If the central or principal maxima in the diffraction pattern of one object or wavelength coincide with the first minima in the diffraction pattern of the other objects or wavelength then the resultant intensity shows a small dip. As shown in the figure below. In this case, the objects or wavelengths are seen to be just separate or just resolved.
Attenuation of optical signal in optical fibre
Attenuation (or Loss) of optical signal in optical Fibre:
The difference in the power of the input optical signals and output optical output signals in optical fibre is known as attenuation in the optical fibre. It is measured in decibels per kilometer $(\frac{dB}{Km})$ and caused by the absorption and scattering of the optical signal in optical fibre.
The optical signal strength is reduced when the signal travels in optical fibre over a long distance. The expression for the attenuation of optical signal in optical fibre:
$\alpha = - \frac{10}{x(Km)} log \left[ \frac{P_{x}}{P_{\circ}} \right]$
Where
$P_{x} \rightarrow $ Power of optical signal at a position $x$ from origin
$P_{\circ} \rightarrow $ Power of optical signal at origin
The Losses in optical fibre are wavelength-dependent and the attenuation factor depends on the fibre material and manufacturing tolerance.
Types of Attenuation or Loss
A.) Absorption Attenuation or Loss
B.) Scattering Attenuation or Loss
C.) Bending Attenuation or Loss
A.) Absorption Attenuation or Loss:
The absorption of optical signals in optical fibre depends on the amount of the material in optical fibre. There are two types of absorption on optical fibre:
1.) Intrinsic Material Absorption
2.) Extrinsic Material Absorption
1.) Intrinsic Material Absorption: It is a fundamental minimum loss due to absorption when the optical signal passes through the optical fibre. This absorption occurs due to material in optical fibre with no impurities.
2.) Extrinsic Material Absorption: It is a loss due to absorption when the optical signal passes through the optical fibre. This absorption occurs due to a material having impurities ( such as $Fe^{+2}, Cu^{+2}, Cr^{+3}, and \: OH^{-}$ ion from water dissolved in glass) in the optical fibre material.
B.) Scattering Attenuation or Loss:
When the optical signal interacts with a particle then the energy of the optical signal is reduced and it goes in another direction. In scattering, the optical signal is not absorbed but it goes to any other direction which also causes the loss of the optical signal. Scattering is the loss of optical signal due to imperfections in the optical fibre i.e. the basic structure of the optical fibre. There are two types of scattering that occur in the optical fibre i.e.
1.) Linear Scattering:
2.) Nonlinear Scattering
1.) Linear Scattering: The amount of power of the optical signal transferred from an optical wave is proportional to power. There is no change in the frequency of the optical signal.
Types of Linear Scattering
i.) Rayleigh scattering in optical fibre
ii.) Mie scattering in optical fibre
i.) Rayleigh scattering in optical fibre: When the optical signal interacts with the lattice of the core it causes the scattering because the size of the lattice is smaller than the wavelength of the incident optical signal. This interaction is also known as elastic scattering.
In optical fibres, This scattering controls the intrinsic loss mechanism in the low-absorption between absorption tails of the ultraviolet and infrared. This is caused by random heterogeneity in the material of the core lattice that leads to changes in the refractive index. These changes cause attenuation in the optical signal by scattering in optical fibre.
ii.) Mie scattering in optical fibre: When the optical signal interacts with the lattice of the core that causes the scattering because in this scattering the size of a lattice is comparable to the wavelength of the incident optical signal. This interaction is also known as elastic scattering.
In optical fibres, This scattering occurs when the optical signal interacts with inhomogeneities in the fibre core or cladding that are larger than the wavelength of the incident optical signal.
2.) Nonlinear scattering: It is an inelastic scattering that occurs when an optical signal interacts with a material in a non-linear manner. Non-linear scattering occurs, when the intensity of the incident optical signal is very high to change the refractive index of material or when the optical signal interacts with molecules or particles that have non-linear optical properties.
In non-linear scattering, the intensity of the scattered optical signal is not proportional to the intensity of the incident optical signal, and the scattered optical signal can be polarized in different planes than the incident optical signal.
In other words,
In non-linear scattering the wavelength, frequency, or phase of scattered optical signal is different than the incident optical signal. The energy and momentum of the scattered optical signal are not conserved, hence, the scattered optical signal has different characteristics than the incident optical signal.
Types of Non-linear Scattering:
i.) Raman Scattering
ii.) Brillouin Scattering
iii.) Self-phase modulation (SPM)
iv.) Cross-phase modulation (XPM)
v.) Four-wave mixing (FWM)
i.) Raman Scattering: It is an inelastic scattering that occurs when a photon of optical signal interacts with molecules of vibrational modes in the material of the core then this photon excites the molecule to a virtual state before being re-emitted in a different direction with a different energy and frequency.
The frequency shift of the scattered optical signal is directly related to the molecule's vibrational energy, which is a characteristic property of the material.
Stimulated Raman scattering $(SRS)$ is an optical process (i.e. nonlinear process ) that enhances scattering by stimulating the molecules of vibrational modes. In SRS, a pump beam of high intensity is used to amplify the Raman signal which leads to a strong and more easily detectable output optical signal.
ii.) Brillouin Scattering: It is an inelastic scattering that occurs when an optical signal interacts with a material, usually a solid or a liquid, causing the material to vibrate.
It can also be said to be a scattering that occurs due to the interaction of an incident optical signal with the acoustic wave in a material.
The vibrating material scatters the optical signal, shifting its frequency by an amount proportional to the frequency of the vibration.
The scattering of the light by the vibrating material is called the Brillouin scattering. This scattering can be either stimulated or spontaneous. It depends on the material that is excited by an external stimulus or its own oscillations.
Stimulated Brillouin scattering (SBS) is used to control the optical signals in optical fibers and other waveguides. When the frequency of the incident optical signal is tuned to the frequency of the vibrational modes of the fiber then the scattered optical signal is shifted to a new frequency which allows for attenuation or amplification of the optical signal.
Brillouin scattering has various applications in materials science. It is used to study the mechanical properties of materials and to determine the stress and strain in solid materials.
iii.) Self-phase modulation (SPM): It is a non-linear effect that occurs when the optical signal of high intensity travels through an optical fiber. The intensity of the optical signal causes a change in the refractive index of the optical fiber that causes a phase shift in the optical signal.
This phase shift can cause the optical signal to spread out in time and frequency which leads to distortion of the transmitted signal.
In other words, The optical signal pulses change their spectrum due to their own intensity from an induced varying refractive index of the medium.
iv.) Cross-phase modulation (XPM): It is a non-linear effect that occurs when two optical signals, typically from two different channels, interact with each other in an optical fiber.
The interaction between the optical signals causes a change in the refractive index of the fiber, that causes a phase shift in one of the optical signals.
This phase shift can distort the optical signal which can lead to crosstalk between different channels in a fiber optic communication system.
v.) Four-wave mixing (FWM): It is a non-linear effect that occurs when two or more incident optical signals interact with each other in a non-linear medium and produce a new wave with a different frequency and phase.
It is used for wavelength conversion of optical signals and signal processing in optical fibers.
C.) Bending Attenuation or Loss: It is caused by the bending of optical fibre or physical stress on the fibre.
Types of Bend Loss
a.) Microbend Loss
b.) Macrobend Loss
a.) Microbend Loss: It is caused by small discountinuities or imperfections in the optical fibre. Microbend loss increses due uneven coating applications and improper cabling procedures. The external force is also a source of micro bending.
b.) Macrobend Loss: It is caused when the fibre bend's radius of curvature is larger than the fibre diametre. These bends are a great source of loss when the radius of curvature is less than several centimetres.
$P_{x} \rightarrow $ Power of optical signal at a position $x$ from origin
$P_{\circ} \rightarrow $ Power of optical signal at origin
B.) Scattering Attenuation or Loss
C.) Bending Attenuation or Loss
2.) Extrinsic Material Absorption
2.) Nonlinear Scattering
ii.) Mie scattering in optical fibre
ii.) Brillouin Scattering
iii.) Self-phase modulation (SPM)
iv.) Cross-phase modulation (XPM)
v.) Four-wave mixing (FWM)
b.) Macrobend Loss
Popular Posts
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(11)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(2)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(5)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(2)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(37)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)



.jpg)







