What is the energy density in the electromagnetic wave in free space?
The total energy stored in electromagnetic waves per unit volume due to the electric field and the magnetic field is called energy density in the electromagnetic wave in free space.
$U=\epsilon_{0} E^{2}=\frac{B^{2}}{\mu_{0}}$
Derivation of Energy density in electromagnetic waves in free space:
The energy per unit volume due to the electric field is
$U_{E}= \frac{1}{2} \overrightarrow{E}.\overrightarrow{D} \qquad(1)$
The energy per unit volume due to the magnetic field is
$U_{B}= \frac{1}{2} \overrightarrow{B}.\overrightarrow{H} \qquad(2)$
The total energy density of electromagnetic waves is
$U=U_{E}+U_{B} \qquad(3)$
Now substitute the value of $U_{E}$ and $U_{B}$ in equation$(3)$ then we get
$U=\frac{1}{2} \left( \overrightarrow{E}.\overrightarrow{D}+\overrightarrow{B}.\overrightarrow{H} \right)$
$U=\frac{1}{2} \left( \overrightarrow{E}.\epsilon_{0}\overrightarrow{E}+\overrightarrow{B}.\frac{1}{\mu_{0}}\overrightarrow{B} \right) \qquad ( \because \overrightarrow{B}= \mu_{0} \overrightarrow{H} \:OR \: \overrightarrow{D}= \epsilon_{0}\overrightarrow{E} )$
$U=\frac{1}{2} \left( \epsilon_{0} E^{2}+\frac{B^{2}}{\mu_{0}} \right) \qquad ( \because \overrightarrow{E}\overrightarrow{E}= E^{2} \:OR \: \overrightarrow{B}.\overrightarrow{B}=B^{2})$
$U=\frac{1}{2} \left( \epsilon_{0} E^{2}+\frac{E^{2}}{c^{2} \mu_{0}} \right) \qquad ( \because B=\frac{E}{c})$
$U=\frac{1}{2} \left( \epsilon_{0} E^{2}+\frac{E^{2}}{c^{2} \mu_{0}} \right) $
$U=\frac{1}{2} \left( \epsilon_{0} E^{2}+\epsilon_{0} E^{2} \right) \qquad ( \because c=\frac{1}{\sqrt{\mu_{0} \epsilon_{0}}})$
$U=\frac{1}{2} \left(2 \epsilon_{0} E^{2} \right) $
$U= \epsilon_{0} E^{2} $
Similarly, the energy density of electromagnetic waves in free space in terms of the magnetic field $B$ can be written as:
$U= \frac{B^{2}}{\mu_{0}} $
The average value of energy density in the electromagnetic waves in free space:
Now we will find the average value of energy density in the electromagnetic wave in free space from the above equation $U= \epsilon_{0} E^{2} $. So we get
$\left< U \right> = \epsilon_{0} \left< E^{2} \right>$
$\left< U \right> = \epsilon_{0} \frac{E_{0}^{2}}{2} \qquad \left (\because \left< E^{2} \right>=\frac{E_{0}^{2}}{2} \right)$
$\left< U \right> = \epsilon_{0} E_{rms}^{2} \qquad \left (\because E_{rms}^{2}=\frac{E_{0}^{2}}{2} \right) \qquad (4)$
We know that
$\left< \overrightarrow{S} \right> = \frac{E_{rms}^{2}}{Z_{0}} .\hat{n} \qquad (5)$
Now divide the equation $(5)$ by equation$(4)$
$\frac{\left< \overrightarrow{S} \right>}{\left< U \right>}=\frac{\frac{E_{rms}^{2}}{Z_{0}} .\hat{n}}{\epsilon_{0} E_{rms}^{2}}$
$\frac{\left< \overrightarrow{S} \right>}{\left< U \right>}=\frac{\hat{n}}{\epsilon_{0} Z_{0}}$
$\frac{\left< \overrightarrow{S} \right>}{\left< U \right>}=\frac{\hat{n}}{\sqrt{\epsilon_{0} \mu_{0}}} \qquad(\because z_{0}= \sqrt{\frac{\mu_{0}}{\epsilon_{0}}})$
$\frac{\left< \overrightarrow{S} \right>}{\left< U \right>}=\hat{n} c \qquad(\because c= \frac{1}{\sqrt{\mu_{0} \epsilon_{0}}})$
$ \left< \overrightarrow{S} \right>=\hat{n} c \left< U \right> $
The energy flow per unit area per unit time in an electromagnetic wave is the product of energy density, speed of light, and the direction of propagation.
The ratio of the energy densities of the electric field and magnetic field:
So from above equation $U_{E}=\epsilon_{0} E^{2}$ and equation $U_{B}=\frac{B^{2}}{\mu_{0}}$, we can find the ratio between them i.e.
$\frac{U_{E}}{U_{B}}=\frac{\epsilon_{0} E^{2}}{\frac{B^{2}}{\mu_{0}}}$
$\frac{U_{E}}{U_{B}}=\frac{\epsilon_{0} \mu_{0} E^{2}}{B^{2}}$
$\frac{U_{E}}{U_{B}}=\frac{c^{2}}{c^{2}}$
$\frac{U_{E}}{U_{B}}=1$
$U_{E}=U_{B}$
So the energy density of the electric field is the same as the energy density of the magnetic field.
Poynting Vector and Poynting Theorem
Poynting Vector:
$\overrightarrow{S}=\frac{1} {\mu_{0}} (\overrightarrow{E} \times \overrightarrow{B})$
Poynting Theorem (Work energy theorem):
The most important aspect of electrodynamics is:
$W=\overrightarrow{J}.\overrightarrow{E} \qquad(1)$
This work done also consider as energy dissipation per unit volume. This energy dissipation must be connected with the net decrease in energy density and energy flow out of the volume. According to Modified Maxwell's Forth equation:
$\overrightarrow{\nabla} \times \overrightarrow{H} = \overrightarrow{J} + \frac{\partial \overrightarrow{D} }{\partial t}$
$\overrightarrow{J} = \overrightarrow{\nabla} \times \overrightarrow{H} - \frac{\partial \overrightarrow{D} }{\partial t} \qquad (2)$
Now subtitute the value of $\overrightarrow{J}$ in equation $(1)$. Therefore we get
$W=\overrightarrow{E}.\left( \overrightarrow{\nabla} \times \overrightarrow{H} - \frac{\partial \overrightarrow{D} }{\partial t}\right) \qquad(3) $
Now we employ the vector identity
$\overrightarrow{\nabla}. (\overrightarrow{E} \times \overrightarrow{H})= \overrightarrow{H} (\overrightarrow{\nabla} \times \overrightarrow{E})-\overrightarrow{E}.(\overrightarrow{\nabla} \times \overrightarrow{H})$
$\overrightarrow{E}.(\overrightarrow{\nabla} \times \overrightarrow{H}) = \overrightarrow{H} (\overrightarrow{\nabla} \times \overrightarrow{E})-\overrightarrow{\nabla}. (\overrightarrow{E} \times \overrightarrow{H})\qquad (4)$
From equation $(3)$ and equation $(4)$
$ W= \overrightarrow{H} (\overrightarrow{\nabla} \times \overrightarrow{E})-\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) - \overrightarrow{E} \left( \frac{\partial \overrightarrow{D} }{\partial t}\right) $
$ W= \overrightarrow{H} \left( \frac{-\partial \overrightarrow{B} }{\partial t}\right)-\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) - \overrightarrow{E} \left( \frac{\partial \overrightarrow{D} }{\partial t}\right) $
$ W= -\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) -\overrightarrow{H} \left( \frac{-\partial \overrightarrow{B} }{\partial t}\right) - \overrightarrow{E} \left( \frac{\partial \overrightarrow{D} }{\partial t}\right) $
$ W= -\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) -\frac{1}{2}\left [2 \overrightarrow{H} \left( \frac{-\partial \overrightarrow{B} }{\partial t}\right) + 2 \overrightarrow{E} \left( \frac{\partial \overrightarrow{D} }{\partial t}\right) \right] $
$ W= -\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) -\frac{1}{2}\left [ \overrightarrow{H} \left( \frac{\partial \overrightarrow{B} }{\partial t}\right)+\overrightarrow{H} \left( \frac{\partial \overrightarrow{B} }{\partial t}\right) + \overrightarrow{E} \left( \frac{\partial \overrightarrow{D} }{\partial t}\right)+ \overrightarrow{E} \left( \frac{\partial \overrightarrow{D} }{\partial t}\right) \right] $
Put $B=\mu H$ and $D=\epsilon E$ in the above equation
$ W= -\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) -\frac{1}{2}\left [ \overrightarrow{H} \left( \frac{\partial \overrightarrow{B} }{\partial t}\right)+\frac{\overrightarrow{B}}{\mu} \left( \frac{\partial \left(\mu \overrightarrow{H}\right) }{\partial t}\right) + \overrightarrow{E} \left( \frac{\partial \overrightarrow{D} }{\partial t}\right)+ \frac{\overrightarrow{D}}{\epsilon} \left( \frac{\partial \left( \epsilon \overrightarrow{E}\right) }{\partial t}\right) \right] $
$ W= -\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) -\frac{1}{2}\left [ \overrightarrow{H} \left( \frac{\partial \overrightarrow{B} }{\partial t}\right)+\overrightarrow{B} \left( \frac{\partial \overrightarrow{H} }{\partial t}\right) + \overrightarrow{E} \left( \frac{\partial \overrightarrow{D} }{\partial t}\right)+ \overrightarrow{D} \left( \frac{\partial \overrightarrow{E} }{\partial t}\right) \right] $
$ W= -\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) -\frac{1}{2}\left [ \frac{ \partial \left(\overrightarrow{B}.\overrightarrow{H}\right) }{\partial t} + \frac{ \partial \left( \overrightarrow{E}.\overrightarrow{D}\right) }{\partial t} \right] $
$ W= -\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) - \frac{1}{2} \frac{\partial}{\partial t} \left( \overrightarrow{H}.\overrightarrow{B}+\overrightarrow{E}.\overrightarrow{D} \right) $
$ JE= -\overrightarrow{\nabla}.(\overrightarrow{E} \times \overrightarrow{H}) - \frac{\partial}{\partial t} \left( \frac{\overrightarrow{H}.\overrightarrow{B}+\overrightarrow{E}.\overrightarrow{D} }{2} \right) \qquad \left( \because W= \overrightarrow{J}.\overrightarrow{E} \right) $
$ -JE= \overrightarrow{\nabla}.\overrightarrow{S} + \frac{\partial}{\partial t} \left( \frac{\overrightarrow{H}.\overrightarrow{B}+\overrightarrow{E}.\overrightarrow{D} }{2} \right) \qquad (\because \overrightarrow{S}= \overrightarrow{E} \times \overrightarrow{H})$
$ -JE= \overrightarrow{\nabla}.\overrightarrow{S} + \frac{\partial U}{\partial t} \qquad \left( \because U = \frac{\overrightarrow{H}.\overrightarrow{B}+\overrightarrow{E}.\overrightarrow{D} }{2} \right) $
$ \overrightarrow{\nabla}.\overrightarrow{S} + \frac{\partial U}{\partial t} =-JE $
This equation represents the conservation of energy principle. It is also known as Poynting theorem. Here Negative signs of work done to represent that electromagnetic flow with energy flux as continuity energy density. So this equation is also known as the continuity equation.
Where
$ \overrightarrow{\nabla}.\overrightarrow{S}$ $\rightarrow$ The flow of energy
$U$ $\rightarrow$ Energy density of electromagnetic filed
$S$ $\rightarrow$ Energy flux or Poyting vector
If Current density $\overrightarrow{J}=0$ Then
$ \overrightarrow{\nabla}.\overrightarrow{S} + \frac{\partial U}{\partial t} = 0 $
$ \overrightarrow{\nabla}.\overrightarrow{S} = \frac{\partial U}{\partial t} $
$ \overrightarrow{\nabla}.\overrightarrow{S} = \frac{\partial }{\partial t} (Storage \: energy) $
The rate of flow of energy per unit area in plane electromagnetic wave is known as Poynting vector. It is represented by $\overrightarrow{S}$. It is a vector quantity.$\overrightarrow{S}=\overrightarrow{E} \times \overrightarrow{H}$
- Energy density stored with an electromagnetic wave
- Energy Flux associated with an electromagnetic wave
Special Relativity- MCQ
Special Relativity- MCQ
You'll have 60 seconds to answer each question.
Time's Up
score:
Test Result
Total Questions:
Attempt:
Correct:
Wrong:
Percentage:
Characteristic impedance of electromagnetic wave
We know that the electromagnetic wave propagates perpendicular to both electric field and magnetic field which can describe as
$\overrightarrow{k} \times \overrightarrow{E}= \omega \overrightarrow{B} \qquad(1)$
If $\hat{n}$ is a unit vector in the direction of the propagation then
$\overrightarrow{k}=k \hat{n}$
Substitute these values in equation$(1)$ then we get
$k(\hat{n} \times \overrightarrow{E})= \omega \overrightarrow{B}$
$\overrightarrow{B}= \frac{k}{\omega}(\hat{n} \times \overrightarrow{E}) \qquad(2)$
But the value of $k$ and $\omega$ is
$k=\frac{2\pi}{\lambda}$
$\omega=2 \pi \nu$
Then value of $\frac{k}{\omega}=\frac{1}{c}$
Now substitute the value of $\frac{k}{\omega}$ in equation$(2)$ then we get
$\overrightarrow{B}= \frac{1}{c}(\hat{n} \times \overrightarrow{E})$
The magnitude form of the above equation can be written as
$B=\frac{E}{c}$
$\frac{E}{B}=c$
$\frac{E}{\mu_{0}H}=c \qquad (\because B=\mu_{0} H)$
$\frac{E}{H}=\mu_{0}c$
$\frac{E}{H}=\frac{\mu_{0}}{\sqrt{\mu_{0} \epsilon_{0}}} \qquad(\because c=\frac{1}{\sqrt{\mu_{0} \epsilon_{0}}})$
$\frac{E}{H}= \sqrt{\frac{\mu_{0}}{\epsilon_{0}}}$
The term $\frac{E}{H}$ has dimensions of the impedance and is known as characteristic impedance or intrinsic impedance of free space. It is represented by $(Z_{0})$.
$Z_{0}=\frac{E}{H}=\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}$
Now substitute the value of $\mu_{0}$ and $\epsilon_{0}$ i.e.
$\mu_{0}=4\pi \times 10^{-7}$
$\epsilon_{0}=8.854 \times 10^{-12}$
$Z_{0}=\sqrt{\frac{4\pi \times 10^{-7}}{8.854 \times 10^{-12}}}$
$Z_{0}=376.73\: \Omega $
$Z_{0}=120\pi \: \Omega $
Radiation pressure of electromagnetic wave
When an electromagnetic wave strikes a surface then its momentum changes. the rate of change of momentum is equal to the applied force. this force acting on the unit area of the surface exerts a pressure called radiation pressure$(P_{rad})$.
Let us consider a plane electromagnetic wave incident normally on a perfectly absorbing surface of area $A$ for a time $t$. If energy $U$ is absorbed during this time then momentum $P$ delivered to the surface is given according to Maxwell's prediction by
$P=\frac{U}{C} \qquad(1)$
If $S$ is the energy flow per unit area per unit time i.e. Poynting vector then the energy density
$U=SAt \qquad(2)$
From equation $(1)$ and equation $(2)$
$P=\frac{SAt}{c}$
$P=UAt \qquad (\because U=\frac{S}{c})$
$\frac{P}{t}=UA \qquad (3)$
If average force $(F)$ acting on the surface, is equal to the average rate of change of momentum $(P)$, is delivered to the surface then
$F=\frac{P}{t} \qquad(4)$
Now from equation$(3)$ and equation$(4)$ we get
$F=UA \qquad(5)$
The radiation pressure $(P_{rad})$ exerted on the surface is
$P_{rad}=\frac{F}{A} \qquad(6)$
Now substitute the value of $F$ from equation$(5)$ in equation$(6)$ then we get
$P_{rad}=\frac{UA}{A}$
$P_{rad}=U$
Hence, the radiation pressure exerted by a normally incident play electromagnetic wave on a perfect absorber is equal to the energy density of the wave.
For a perfect reflector or for a perfect reflecting surface, the radiation after reflection has momentum equal in magnitude but opposite in direction to the incident radiation. Then the momentum imparted to the surface will therefore be twice as on perfect absorber i.e.
$P_{rad}=2U$
Physical interpretation of the wave function
We have assumed that the wave associated with a particle in motion is represented by a complex variable quantity called the wave function $\psi(x,t)$. Therefore, it can not have a direct physical meaning. Since it is a complex quantity, it may be expressed as
$\psi(x,y,z,t)=a+ib \qquad(1)$
Where $a$ and $b$ are real functions of the variable $(x,y,z,t)$. The complex conjugate of wave function $\psi(x,y,z,t)$
$\psi^{*}(x,y,z,t)=a-ib \qquad(2)$
Multiply equation $(1)$ and equation $(2)$
$\psi(x,y,z,t).\psi^{*}(x,y,z,t)=a^{2}+b^{2} \qquad(3)$
$ \left| \psi(x,y,z,t) \right|^{2}=a^{2}+b^{2} \qquad(4)$
If $\psi \neq 0$ Then the product of $\psi$ and $\psi^{*}$ is real and positive. Its positive square root is denoted by $\left|\psi(x,y,z,t) \right|$, and it is called the modulus of $\psi$.
The quantity $ \left| \psi(x,y,z,t) \right|^{2}$ is called the probability density $(P)$. So for the motion of a particle, the probability of finding the particle in the region $d\tau$ will be:
$\int {P d\tau}= \int {\psi(x,y,z,t).\psi^{*}(x,y,z,t).d\tau}=\int {\left| \psi(x,y,z,t) \right|^{2}d\tau}$
Here $P$ are the probability that tells us that the particle will be found in a volume element $d\tau(=dx.dy.dz)$ surrounding the point at position $(x,y,z)$ at time $t$.
For the motion of a particle in one dimension, the probability of finding the particle in the region $dx$ will be:
$\int{P dx}= \int {\psi(x,t).\psi^{*}(x,t).dx}=\int {\left| \psi(x,t) \right|^{2}dx}$
Energy flow in the electromagnetic wave in free space
Derivation of energy flow in the electromagnetic wave in free space:
The Poynting vector is given by
$\overrightarrow{S}=\overrightarrow{E} \times \overrightarrow{H} \qquad(1)$
$\overrightarrow{S}=\frac{1}{\mu_{0}} ( \overrightarrow{E} \times \overrightarrow{B} ) \qquad(2) \qquad (\because \overrightarrow{B}= \mu_{0} \overrightarrow{H})$
We know that the characteristic impedance equation i.e.
$\overrightarrow{B}=\frac{1}{\mu_{0}c}(\hat{n} \times \overrightarrow{E}) \qquad(3)$
Now substitute the value of $\overrightarrow{B}$ in equation$(2)$
$\overrightarrow{S}=\frac{1}{\mu_{0}c} [\overrightarrow{E} \times (\hat{n} \times \overrightarrow{E})]$
$\overrightarrow{S}=\frac{1}{\mu_{0}c} [(\overrightarrow{E}.\overrightarrow{E}) \hat{n}- (\overrightarrow{E}.\hat{n}) \overrightarrow{E})] \qquad(4)$
As $\overrightarrow{E}$ is perpendicular to $\hat{n}$ so $\overrightarrow{E} . \hat{n}=0$ then we get for above equation$(4)$
$\overrightarrow{S}=\frac{1}{\mu_{0}c} E^{2} \hat{n}$
From the above equation, we can conclude $\overrightarrow{S}$ has the same direction as $\hat{n}$ which is the direction of wave propagation.
Energy flow in an electromagnetic wave takes place in the direction of the propagation of the wave.
Here $\mu_{0} c=Z_{0}$ (The Characteristic impedance of free space)
$\overrightarrow{S}=\frac{1}{Z_{0}} E^{2} \hat{n}$
This is the equation of energy flow in the electromagnetic wave in free space.
The average energy flow over one period of the electromagnetic wave in free space:
Now the average energy flow of the above equation
$ \left< \overrightarrow{S} \right> =\frac{1}{Z_{0}} \left< E^{2} \right> \hat{n} \qquad(5)$
We know the electric field vector wave equation i.e. $\overrightarrow{E}=E_{0} e^{i(\overrightarrow{k}. \overrightarrow{r} -\omega t)} $
So the value of $\left< E^{2} \right>$ from above equation:
$\left< E^{2} \right>= \left< Re[E_{0} e^{i(\overrightarrow{k}. \overrightarrow{r} -\omega t)}]^{2} \right>$
$\left< E^{2} \right>= \left< E_{0}^{2}\: cos^{2}(\overrightarrow{k}. \overrightarrow{r} -\omega t) \right>$
For one period or cycle of electromagnetic wave the value of $cos^{2}(\overrightarrow{k}. \overrightarrow{r} -\omega t)=\frac{1}{2}$ then we get
$\left< E^{2} \right>= \frac{E_{0}^{2}}{2}$
$\left< E^{2} \right>= (\frac{E_{0}}{2})^{2}$
$\left< E^{2} \right>= E_{rms}^{2} \qquad \left (\because E_{rms} = \frac{E_{0}}{2}\right )$
Now substitute the value of $ \left< E^{2} \right>$ in equation $(5)$ then we get
$ \left< \overrightarrow{S} \right> =\frac{E_{rms}^{2}}{Z_{0}} \hat{n} $
This average energy flow equation over one period of the electromagnetic wave in free space.
Momentum of electromagnetic wave
Derivation of momentum of electromagnetic wave:
Maxwell's had also predicted that electromagnetic waves transport linear momentum in the direction of propagation. Let a particle which has mass $m$ moving with velocity then the momentum of a particle,
$\overrightarrow{P}=m\overrightarrow{v} \qquad(1)$
According to mass-energy relation
$U=mc^{2}$
Here $U$ - Total energy of the particle
$m=\frac{U}{c^{2}} \qquad(2)$
From equation $(1)$ and equation $(2)$
$\overrightarrow{P}=\frac{U}{c^{2}} \overrightarrow{v} \qquad(3)$
If the electromagnetic wave is propagating along the x-axis then
$\overrightarrow{v}=c \hat{i}$
Put this value in the above equation $(3)$
$\overrightarrow{P}=\frac{U}{c} \hat{i} \qquad(4)$
We know that the equation of energy flow in electromagnetic wave
$\overrightarrow{S}= \frac{1}{\mu_{0} c} E^{2} \hat{n}$
Here wave is propagating along x-axis i.e
$\hat{n}=\hat{i}$
$\overrightarrow{S}= \frac{1}{\mu_{0} c} E^{2} \hat{i} \qquad(5)$
The energy density in plane electromagnetic wave in free space:
$U=\epsilon_{0} E^{2}$
Where $E$ - Magnitude of electric field
$E^{2}=\frac{U}{\epsilon_{0}} \qquad(6)$
Now substitute the value of $E^{2}$ in equation$(5)$
$\overrightarrow{S}= \frac{1}{\mu_{0} c} \frac{U}{\epsilon_{0}} \hat{i} $
$\overrightarrow{S}= \frac{c^{2}}{c} U \hat{i} \qquad (\because \frac{1}{\sqrt{ \mu_{0} \epsilon_{0}}}=c) $
$\overrightarrow{S}= c U \hat{i} $
$U \hat{i}=\frac{\overrightarrow{S}}{c} \qquad(7)$
Now substitute the value of $ U \hat{i} $ in equation $(4)$. Then
$\overrightarrow{P}=\frac{\overrightarrow{S}}{c}$
$\overrightarrow{P}=\frac{(\overrightarrow{E} \times \overrightarrow{B})}{ \mu_{0}c^{2}}$
$\overrightarrow{P}=\epsilon_{0}(\overrightarrow{E} \times \overrightarrow{B})$
This is the equation of "Momentum of electromagnetic wave"
Particle in one dimensional box (Infinite Potential Well)
Let us consider a particle of mass $m$ that is confined to one-dimensional region $0 \leq x \leq L$ or the particle is restricted to move along the $x$-axis between $x=0$ and $x=L$. Let the particle can move freely in either direction, between $x=0$ and $x=L$. The endpoints of the region behave as ideally reflecting barriers so that the particle can not leave the region. A potential energy function $V(x)$ for this situation is shown in the figure below.
The potential energy inside the one -dimensional box can be represented as
$\begin{Bmatrix}
V(x)=0 &for \: 0\leq x \leq L \\
V(x)=\infty & for \: 0> x > L \\
\end{Bmatrix}$
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2m}{\hbar^{2}}(E-V)\psi(x)=0 \qquad(1)$
If the particle is free in a one-dimensional box, Schrodinger's wave equation can be written as:
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2mE}{\hbar^{2}}\psi(x)=0$
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{8 \pi^{2} mE}{h^{2}}\psi(x)=0 \quad (\because \hbar=\frac{h}{2 \pi}) \quad(2)$
$\frac{d^{2} \psi(x)}{d x^{2}}+ k^{2}\psi(x)=0 \quad (\because k^{2}=\frac{8 \pi^{2} mE}{h^{2}}) \quad(3)$
The general solution of the above differential equation $(2)$
$\psi(x)= A sin(kx)+ B cos(kx) \qquad(4)$
The wave function $\psi(x)$ should be zero everywhere outside the box since the probability of finding the particle outside the box is zero. Similarly, the wave function $\psi(x)$ must also be zero at walls of the box because the probability density $[\psi(x)]^{2}$ must be continuous. Thus, the boundary conditions for this problem is that
(i) $\psi(x)=0$ For $x=0$
(ii) $\psi(x)=0$ For $x=L$
Now applying the boundary condition in equation$(4)$ i.e.
(i) At $x=0$ the wave function $\psi(0)=0$
Now we get
$\psi(0)= A sin(k.0)+ B cos(k.0)$
$A sin(k.0)+ B cos(k.0)=0 \qquad (\because \psi(0)= 0)$
$B=0$
Hence substitute the value of $B$ in equation$(4)$ ,
$\psi(L)= A sin(kx) \qquad(5)$
Now applying the second boundary condition:
(ii) At $x=L$ the wave function $\psi(L)=0$, we get
$\psi(x)= A sin(kL) \qquad(6)$
This equation will satisfy only for certain values of $k$, say $k_{n}$. Since $A$ can not be taken zero hence
$sin(k_{n}L)=0 $
$sin(k_{n}L)=sin(n\pi) $
$k_{n}L=n\pi $
$k_{n}=\frac{n\pi}{L} \qquad(7)$
Thus for each allowed values of $k_{n}$ there is a wave function $\psi(x)$ given as, using equation$(5)$ and equation$(7)$
$\psi_{n}(x)=A sin(\frac{n\pi x}{L})$
This is the expression of the wave function or eigen function for a particle in a box.
Now, from equation $(3)$ and equation$(7)$, we get
$k^{2}=\frac{8 \pi^{2} mE}{h^{2}}= (\frac{n \pi}{L})^{2}$
$E=\frac{n^{2} h^{2}}{8mL^{2}}$
This is the expression of energy or eigen value for a particle in a box.
In general, the expression for this energy is written as:
$E_{n}=\frac{n^{2} h^{2}}{8mL^{2}}$
For different values of $n$ energy values can be written as
For $n=1$
$E_{1}=\frac{h^{2}}{8mL^{2}}$
It is known as zero-point energy or ground energy state
For $n=2$
$E_{2}=\frac{2^{2} h^{2}}{8mL^{2}}=2^{2}E_{1}$
For $n=3$
$E_{3}=\frac{3^{2} h^{2}}{8mL^{2}}=3^{2}E_{1}$
For $n=4$
$E_{4}=\frac{4^{2} h^{2}}{8mL^{2}}=4^{2}E_{1}$
So generalized form of the above equation can be written as
$E_{n}=n^{2}E_{1}$
Some of the possible energies for a particle in a box are shown on an energy-level diagram in the figure below.
The energy levels have a spacing that increases with increasing $n$ and thus the particle in a box can take only certain discrete energy values, called Eigen-values. This means that the energy levels of a particle in a box are quantized but according to classical mechanics, the particle may take any continuous range of energy values between zero and infinity.
 |
Particle in One-Dimensional Box(Infinite Potential Well) |
 |
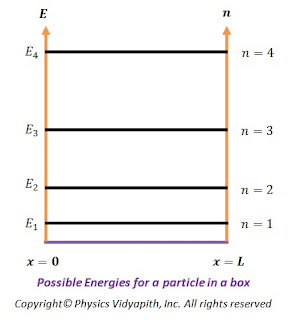Possible Energies for a particle in a box |
Solution of electromagnetic wave equations in free space
The electromagnetic wave equations in free space:
For electric field vector:
$\nabla^{2} \overrightarrow{E}=\frac{1}{c^{2}} \frac{\partial^{2} \overrightarrow{E}}{\partial t^{2}} \qquad(1)$
For magnetic field vector:
$\nabla^{2} \overrightarrow{B}=\frac{1}{c^{2}} \frac{\partial^{2} \overrightarrow{B}}{\partial t^{2}} \qquad(2)$
The wave equation of electric field vector:
$\overrightarrow{E}(\overrightarrow{r},t)=E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(3)$
The wave equation of magnetic field vector:
$\overrightarrow{B}(\overrightarrow{r},t)=B_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(4)$
Now the solution of electromagnetic wave for electric field vector.
Differentiate with respect to $t$ of equation $(3)$
$\frac{\partial \overrightarrow{E}}{\partial t}=i \omega E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$
Again differentiate with respect to $t$ of the above equation:
$\frac{\partial^{2} \overrightarrow{E}}{\partial t^{2}}=i^{2} \omega^{2} E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$
$\frac{\partial^{2} \overrightarrow{E}}{\partial^{2} t}=- \omega^{2} \overrightarrow{E}(\overrightarrow{r},t)$
Now substitute the value of the above equation in equation$(1)$
$\nabla^{2} \overrightarrow{E}=\frac{-\omega^{2}}{c^{2}} \overrightarrow{E}(\overrightarrow{r},t)$
$\nabla^{2} \overrightarrow{E}=-(\frac{\omega}{c})^{2} \overrightarrow{E}(\overrightarrow{r},t)$
$\nabla^{2} \overrightarrow{E}=-k^{2} \overrightarrow{E}(\overrightarrow{r},t) \qquad (\because \frac{\omega}{c}=k )$
Where $k$ - Wave propagation Constant
$\nabla^{2} \overrightarrow{E} + k^{2} \overrightarrow{E}(\overrightarrow{r},t)=0 $
This is the solution of the electromagnetic wave equation in free space for the electric field vector.
Now the component form of the above equation:
$(\frac{\partial^{2}}{\partial x^{2}}
+ \frac{\partial^{2}}{\partial y^{2}} +\frac{\partial^{2}}{\partial z^{2}})(\hat{i}E_{x}+\hat{j}E_{y}+\hat{k}E_{z}) \\ =- k^{2}(\hat{i}E_{x}+\hat{j}E_{y}+\hat{k}E_{z}) \qquad(5)$
If the wave is propagating along $z$ direction. Then for uniform-plane electromagnetic waves-
$\frac{\partial}{\partial x}=\frac{\partial}{\partial y}=0$
$\frac{\partial^{2}}{\partial x^{2}}=\frac{\partial^{2}}{\partial y^{2}}=0$
$E_{z}=0$
Now the equation $(5)$ can be written as:
$\frac{\partial^{2}}{\partial x^{2}}(\hat{i}E_{x}+\hat{j}E_{y})=- k^{2}(\hat{i}E_{x}+\hat{j}E_{y})$
Now separate the above equation in $x$ and $y$ components so
$\frac{\partial^{2} E_{x}}{\partial z^{2}}=- k^{2}E_{x}$
$\frac{\partial^{2}E_{y}}{\partial z^{2}} =- k^{2}E_{y}$
The solution of electromagnetic wave for magnetic field vector can find out by following the above method.
Therefore $x$ and $y$ components of the solution of the electromagnetic wave equation for magnetic field vector can be written as. i.e.
$\frac{\partial^{2} B_{x}}{\partial z^{2}}=- k^{2}B_{x}$
$\frac{\partial^{2}B_{y}}{\partial z^{2}} =- k^{2}B_{y}$
Popular Posts
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t... -
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
