Limitations of Bohr's Model

Although Bohr's model of hydrogen atom and hyarogen like atom was successful in explaining the stability and spectrum even then it has few limitations. which are as follows:

(1) This model could not explain the spectrum of atom having more than one electron.

(2) This model could not explain the relative intensity of spectral lines. (i. e., few transitions are more acceptable than others why?)

(3) When a spectral line is observed by spectroscope of high resolution power, more than one lines are observed. This is known as fine structure of spectral line. Bohr model could not explain this.

(4) Splitting of spectral lines in external magnetic field (Zeeman's effect) and in external electric field (Stark's effect) could not be explained by this model.

(5) This model could not explain the distribution of electrons in different orbit.

Few limitations of Bohr's model are removed in Somer-field's model of atom. (In this model, the orbit of electron was considered as elliptical instead of circular ). But this model also has its limitations. Vector atomic model, which is based on quantum mechanics, explains clearly the structure of atom.

Read More

Comparison of Isothermal and Adiabatic Processes for an Ideal Gas

Isothermal Process:

1.) In this process temperature remains constant i.e.$(\Delta T= 0)$.

2.) In this process internal energy remains constant i.e. $(\Delta U= 0)$.

3.) This process takes place very slowly.

4.) In this process the system is surrounded by a perfectly conducting material, whose conductivity is infinite.

5.) This process obeys Boyle's law i.e. $(PV= constant)$.

6.) In this process the slope of isothermal curve $=-\frac{P}{V}$

7.) In this process specific heat of gas should be infinite.

Adiabatic Process:

1.) In this process exchange of heat does not take place i.e. $(\Delta Q= 0)$ but temperature changes.

2.) In this process internal energy changes.

3.) This process takes place very rapidly.

4.) In this process the system is surrounded by a perfectly insulating material, whose conductivity is zero.

5.) This process obeys Poisson's law i.e. $(PV^{\gamma} = constant)$.

6.) In this process the slope of adiabatic curve $=- \gamma \frac{P}{V}$

7.) In this process specific heat of gas should be zero.

Read More

Concept of Perfect Gas

Concept of Perfect (ideal) Gas:

An imaginary gas whose properties are similar to the properties of a real gas (a gas whose molecules occupy space and interact with each other) at infinitely low pressure. This imaginary gas is called 'perfect gas' or ideal gas'.

According to the definition, the following properties are imagined in a perfect gas :

(1) It strictly obeys Boyle's law, Charles' law, and the law of pressure under all conditions of temperature and pressure.

(2) Its pressure coefficient and volume coefficient are exactly equal to each other.

(2) Its molecules are infinitesimally small.

(3) There is no force of attraction between its molecules. Obviously, a perfect gas cannot be converted into a liquid or solid state, because a force of attraction is necessary between the molecules in the liquid or the solid state.

In practice, the gases that are difficult to liquefy, such as oxygen, nitrogen, hydrogen, and helium can be considered as perfect, although these are also not ideally perfect.

Read More

Failure of Wave Theory in Explaining Photoelectric Emission Effect

Description of failure of wave theory in explaining photoelectric effect:

Although reflection, refraction, interference, diffraction and polarisation etc. are explained on the basis of wave theory but the laws of photoelectric effect cannot be explained on the basis of the wave theory of light. There are three main reasons for failure:

1.) According to wave theory, as the intensity of incident light increases, incident energy also increases. Therefore, greater is the intensity, greater will be the energy absorbed by the electrons of metal and therefore greater should be the kinetic energy of photoelectrons. From experimental observations, it is clear that the maximum kinetic energy of photoelectrons does not depend on the intensity of incident light.

2.) According to wave theory, photoelectric emission should occur for all the frequencies provided that it has enough energy to emit the electrons from the metal. Although from experimental observation it is clear that if the frequency of incident light is less than the threshold frequency, photoelectrons are not emitted.

3.) The energy carried by the light waves is absorbed by all the electrons and not by a single electron. Therefore, if the intensity of light is less, for the emission of electrons, there should be some time to collect sufficient energy. Although it is clear from experimental observation, the electrons are emitted instantaneously, whatever small be the intensity of light.

Read More

Einstein Photoelectric Emission Effect Law

Description of the Light:

According to the Albert Einstein

The light is consist of small packets or bundles of energy. These packets are called photon. The energy of each photon is $h \nu$.

Theory of Photoelectric Effect:

When the photon of ultraviolet ray is incident on the metal then this energy is used in two parts:

1.) To emit the electron from a metal surface i.e. Work Function. The electron emitted from a metal surface is called the photoelectron.

2.) Remaining energy increases the kinetic energy of the emitted photoelectron. This is the maximum kinetic energy of the photoelectron.

Let us consider

The energy of incident Ultraviolet Photon $E=h\nu$

The work function $W= h \nu_{\circ}$

The maximum kinetic energy of photo electron $K_{max}= \frac{1}{2}mv^{2}_{max}$

According to Einstein's photoelectric effect theory

$E=W+K_{max}$

$h \nu = h \nu_{\circ} + \frac{1}{2}m v^{2}_{max}$

$h \nu - h \nu_{\circ} = \frac{1}{2}m v^{2}_{max}$

$h \left( \nu - \nu_{\circ} \right) = \frac{1}{2}m v^{2}_{max}$

Where
$\nu \rightarrow$ Frequency of incident Ultraviolet ray photon
$\nu_{\circ} \rightarrow$ Threshold frequency to emit the photoelectron from the metal surface
$ v_{max} \rightarrow$ Maximum velocity of emitted photoelectron from the metal surface

Read More

Laws of photoelectric emission

There are the following laws of photoelectric emission:

1.) The rate of emission of photoelectrons from the metal surface is directly proportional to the intensity of the incident light on the metal surface.

2.) The maximum kinetic energy of photoelectrons does not depend on the intensity of incident light.

3.) If the frequency of incident light is less than the threshold frequency then no photoelectrons will come out of the surface.

4.) If the frequency of incident light is equal to the threshold frequency then electrons will come out of the surface but the kinetic energy of emitted photoelectrons will be zero.

5.) As the frequency of incident light increases greater than the threshold frequency, the maximum kinetic energy $K_{max}$ of photoelectrons emitted from the metal surface also increases.

6.) The value of threshold frequency depends upon the nature of the metal surface and its value is different for different metals.

7.) There is no time lag in the emission of photoelectrons to the metal surface i.e., as the light of proper from frequency is made to the incident on the metal surface, photoelectrons immediately come out of the surface within no time.

Read More

Expression for fringe width in Young's double slit experiment

Expression for fringe's width:

Let us consider two wave from slit $S_{1}$ and $S_{2}$ superimpose on each other and form interfernece patteren on the screen. The distance between the two slits is $d$ and distance between slit to screen is $D$. Now take a $n^{th}$ fringe from the centre $O$ of the screen which is at distance $y_{n}$.

So the path difference between the rays

$\Delta x = S_{2}P- S_{1}P \quad(1)$

In $\Delta S_{1}PM$

$S_{1}P^{2}=S_{1}M^{2}+PM^{2} \quad(2)$

From figure:

$S_{1}M =D$
$PM= y_{n}- \left(\frac{d}{2}\right) $

Now subtitute these values in equation $(2)$, then

$S_{1}P^{2}=D^{2}+ \left( y_{n}- \frac{d}{2} \right)^{2} \quad(3)$

In $\Delta S_{2}PN$

$S_{2}P^{2}=S_{2}N^{2}+PN^{2} \quad(4)$

From figure:

$S_{2}N =D$
$PN= y_{n} + \left(\frac{d}{2}\right) $

Now subtitute these values in equation $(4)$, then

$S_{2}P^{2}=D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2} \quad(5)$

Now subtract the equation $(3)$ in equation $(5)$

$S_{2}P^{2} - S_{1}P^{2} = \left[D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2}\right] - \left[ D^{2}+ \left( y_{n}- \frac{d}{2} \right)^{2} \right] $

$S_{2}P^{2} - S_{1}P^{2} = D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2} - D^{2} - \left( y_{n}- \frac{d}{2} \right)^{2} $

$S_{2}P^{2} - S_{1}P^{2} = \left( y_{n} + \frac{d}{2} \right)^{2} - \left( y_{n}- \frac{d}{2} \right)^{2} $

$S_{2}P^{2} - S_{1}P^{2} = y^{2}_{n} + \left(\frac{d}{2}\right)^{2} +2 y_{n} \left(\frac{d}{2}\right) - y^{2}_{n} - \left(\frac{d}{2}\right)^{2} +2 y_{n} \left(\frac{d}{2}\right) $

$S_{2}P^{2} - S_{1}P^{2} = y^{2}_{n} + \left(\frac{d}{2}\right)^{2} + y_{n} d - y^{2}_{n} - \left(\frac{d}{2}\right)^{2} + y_{n} d $

$S_{2}P^{2} - S_{1}P^{2} = y_{n} d + y_{n} d $

$ \left( S_{2}P + S_{1}P \right) \left( S_{2}P - S_{1}P \right) = 2y_{n} d$

$ \left( S_{2}P + S_{1}P \right) \Delta x = 2y_{n} d \quad \left\{from \: equation\: (1)\right\} \qquad(6)$

In this experiment, the distance between slit and screen i.e. $D$ is much greater than the distance between the slit i.e. $d$ so angle $\theta$ will be very small. So from figure

$S_{1}P = S_{2}P = D$

Substitute this value in the equation $(6)$, therefore equation $(6)$ can be written as

$ 2D \Delta x = 2y_{n} d $

$D \Delta x = y_{n}$

$\Delta x = \frac{y_{n} d}{D} \quad (7) $

This is equation of path differnce between two wave from slit $S_{1}$ and slit $S_{2}$.

Condition For Bright Fringe:

The path difference for bright fringe is

$\Delta x= n \lambda \qquad(8)$

From equation $(7)$ and equation $(8)$

$n \lambda = \frac{ d}{D} $

$y_{n} = \frac{n \lambda D}{d} \quad(9)$

This is the equation for distance of $n^{th}$ bright fringe. Now the distance of $(n+1)^{th}$ bright fringe.

$y_{n+1} = \frac{\left( n+1 \right) \lambda D}{d} \quad(10)$

The dark fringe lie between the two consecutive bright fringe. So width of the dark fringe

$\beta = y_{n+1} - y_{n}$

Now subtitute the value of $y_{n+1}$ and $y_{n}$ in the above equation $(9)$ and equation $(10)$, then

$\beta = \frac{\left( n+1 \right) \lambda D}{d} - \frac{n \lambda D}{d}$

$\beta = \frac{\lambda D}{d} \quad(11)$

This is the equation of width of dark fringe.

Condition For Dark Fringe:

The path difference for dark fringe is

$\Delta x = (2n-1) \lambda \quad(12)$

From equation $(7)$ and equation $(12)$

$ (2n-1) \lambda = \frac{y_{n} d}{D} $

$y_{n} = \frac{(2n-1) \lambda D}{d} \quad(13)$

This is the equation for distance of $n^{th}$ dark fringe. Now the distance of $(n+1)^{th}$ dark fringe.

$y_{n+1} = \frac{\left[ 2 (n+1)-1) \right] \lambda D}{d} $

$y_{n+1} = \frac{(2n+1)\lambda D}{d} \quad(14)$

The bright fringe lie between the two consecutive dark fringe. So width of the bright fringe

$\beta = y_{n+1} - y_{n}$

Now subtitute the value of $y_{n+1}$ and $y_{n}$ in the above equation $(13)$ and equation $(14)$, then

$\beta = \frac{(2n+1)\lambda D}{d} - \frac{(2n-1) \lambda D}{d}$

$\beta = \frac{\lambda D}{d} \quad(15)$

This is the equation of width of bright fringe.

The equation $(11)$ and equation $(15)$ shows that the width of bright fring and dark fringe is same.

Alternative method to find the path differnce of two wave in Young's double-slit Experiment

Let us consider: Two wave from slit $S_{1}$ and $S_{2}$ superimpose on each other and form interfernece patteren on the screen.

The distance between the two slits is $\rightarrow d$

The distance between slit to screen is $\rightarrow D$

The distance of $n^{th}$ fringe from the centre $O$ of the screen is $\rightarrow y_{n}$.

So the path difference between the two rays is

$\Delta x = S_{2}M \quad(1)$

Now from figure, In $\Delta S_{1}S_{2}M$

$sin \theta = \frac{S_{2}M}{S_{1}S_{2}} \quad(2)$

In $\Delta PNO$

$tan \theta = \frac{PO}{NO} \quad(3)$

The distance between slit and screen i.e. $D$ is much greater than the distance between the slit i.e. $d$ so angle $\theta$ will be very small i.e. $sin \theta \approx tan \theta \approx \theta $. Now equate the equation $(2)$ and equation $(3)$

$\frac{PO}{NO} = \frac{S_{2}M}{S_{1}S_{2}} \quad(4)$

Now the value from the above figure

$\frac{y_{n}}{D} = \frac{\Delta x}{d} $

$\Delta x = \frac{y_{n} d}{D} $

This is the equation of the path difference between two wave from slit $S_{1}$ and $S_{2}$.

Now the derivation for the condition for Bright and Dark fringe can be used here as it is given above.

Read More

Analytical expression of intensity for constructive and destructive interference due to Young's double slit

Analytical expression of intensity for interference due to Young's double slit:

Let us consider two waves from slit $S_{1}$ and $S_{2}$ having amplitude $a_{1}$ and $a_{2}$ respectively superimpose on each other at point $P$ . If the displacement of waves is $y_{1}$ and $y_{2}$ and the phase difference is $\phi$ then

$y_{1}=a_{1} \: sin \omega t \qquad(1)$

$y_{2}=a_{2} \: sin \left( \omega t + \phi \right) \qquad(2)$

According to the principle of superposition:

$y=y_{1}+y_{2} \qquad(3)$

Now substitute the value of $y_{1}$ and $y_{2}$ in the above equation $(3)$

$y=a_{1} \: sin \omega t + a_{2} \: sin \left( \omega t + \phi \right)$

$y=a_{1} \: sin \omega t + a_{2} \left( sin \omega t \: cos \phi + cos \omega t \: sin \phi \right) $

$y=a_{1} \: sin \omega t + a_{2} \: sin \omega t \: cos \phi + a_{2}\: cos \omega t \: sin \phi $

$y= \left( a_{1} + a_{2} \: cos \phi \right) \: sin \omega t + a_{2} \: sin \phi \: cos \omega t \qquad(4)$

Let

$a_{1} + a_{2} \: cos \phi = A\: cos\theta \qquad(5)$

$a_{2} \: sin \phi = A\: sin\theta \qquad(6)$

Now the above equation $(4)$ can be written as

$y= A\: cos\theta \: sin \omega t + A\: sin\theta \: cos \omega t $

$y= A \left( cos\theta \: sin \omega t + sin\theta \: cos \omega t \right)$

$y= A \: sin \left( \omega t + \theta \right) \qquad(7)$

This is the equation of the resultant displacement of the waves from slit $S_{1}$ and $S_{2}$ at point $P$ on the screen.

Now square the equation $(5)$ and equation $(6)$ and then add to them so

$ A^{2} \: sin^{2}\theta + A^{2}\: cos^{2}\theta = \left( a_{1} + a_{2} \: cos \phi \right)^{2} + a^{2}_{2} \: sin^{2} \phi $

$ A^{2} \left( sin^{2}\theta + cos^{2}\theta \right) = a^{2}_{1} + a^{2}_{2} \: cos^{2} \phi + 2a_{1} \: a_{2} \: cos\phi + a^{2}_{2} \: sin^{2} \phi $

$ A^{2} = a^{2}_{1} + a^{2}_{2} \left( cos^{2}\phi + sin^{2}\phi \right) + 2a_{1} \: a_{2} \: cos\phi $

$ A^{2} = a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi \qquad(8)$

$ A = \sqrt{ a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi }\qquad(9)$

Resultant Intensity:

The resultant intensity at point $P$ due waves from slit $S_{1}$ and $S_{2}$ can be find by flollowing formula:

$I=A^{2}$

Now subtitute the va;ue of $A^{2}$ from equation $(8)$ in the above equation

$I= a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi \qquad(10)$

$I= I_{1} + I_{2} + 2\sqrt{I_{1} \: I_{2}} \: cos\phi \qquad(11)$

Constructive Interference:

For constructive interference the $cos\phi$ should be equal to +1 i.e. $cos\phi =1$

Phase Difference in Constructive Interference:

We know that for constructive interference $cos\phi =1$

$cos\phi = cos( 2n\pi)$

$\phi = 2n\pi \qquad(12)$

Path difference in Constructive Interference:

We know that the path difference

$\Delta x = \frac{\lambda}{2 \pi} \phi$

Now subtitute the value of $\phi $ from equation $(12)$ in the above equation

$\Delta x = \frac{\lambda}{2 \pi} 2n\pi$

$\Delta x = n \lambda \qquad(13)$

Resultant Amplitude due to Constructive Interference:

For constructive interference, the resultant amplitude is maximum at point $P$. So from equation $(9)$

$ A_{max} = \sqrt{ a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} } \qquad \left( \because cos\phi =+1 \right)$

$ A_{max} = \sqrt{ \left (a_{1} + a_{2} \right)^{2}} $

$ A_{max} = \left( a_{1} + a_{2} \right) \qquad(14)$

For constructive interference, the resultant amplitude of the waves is the sum of the amplitude of individual waves.

Resultant Intensity due to Constructive Interference:

For constructive interference, the resultant intensity is maximum at point $P$. So from equation $(10)$

$I_{max}= a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \qquad \left( \because cos\phi =+1 \right)$

$I_{max}=\left( a_{1} + a_{2} \right)^{2} \qquad(15)$

From equation $(11)$

$I_{max}= I_{1} + I_{2} + 2\sqrt{I_{1} \: I_{2}} \qquad(16)$

Destructive Interference:

For destructive interference the $cos\phi$ should be equal to -1 i.e. $cos\phi = -1$

Phase Difference in Destructive Interference:

We know that for destructive interference $cos\phi = -1$

$cos\phi = cos \left( \left( 2n \pm 1 \right)\pi \right)$

$\phi = \left( 2n \pm 1 \right)\pi \qquad(17)$

Path difference in Destructive Interference:

We know that the path difference

$\Delta x = \frac{\lambda}{2 \pi} \phi$

Now subtitute the value of $\phi $ from equation $(17)$ in the above equation

$\Delta x = \frac{\lambda}{2 \pi} \left( 2n \pm 1 \right)\pi$

$\Delta x = \left( 2n \pm 1 \right) \frac{\lambda}{2} \qquad(18)$

Resultant Amplitude due to Destructive Interference:

For the destructive interference, the resultant amplitude is minimum at point $P$. So from equation $(9)$

$ A_{min} = \sqrt{ a^{2}_{1} + a^{2}_{2} - 2a_{1} \: a_{2} } \qquad \left( \because cos\phi =-1 \right)$

$ A_{min} = \sqrt{ \left (a_{1} - a_{2} \right)^{2}} $

$ A_{min} = \left( a_{1} - a_{2} \right)$

For constructive interference, the resultant amplitude of the waves is the difference in amplitude of individual waves.

Resultant Intensity due to Destructive Interference:

For the destructive interference, the resultant intensity is minimum at point $P$. So from equation $(10)$

$I_{min}= a^{2}_{1} + a^{2}_{2} - 2a_{1} \: a_{2} \qquad \left( \because cos\phi =-1 \right)$

$I_{min}=\left( a_{1} - a_{2} \right)^{2}$

From equation $(11)$

$I_{min}= I_{1} + I_{2} - 2\sqrt{I_{1} \: I_{2}} $

Read More

Viscosity, Viscous force and Coefficient of Viscosity

Definition of Viscosity:

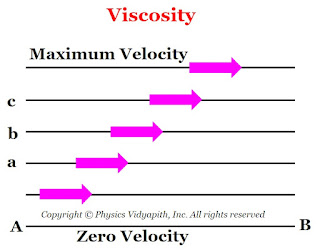
It is the property of a fluid that opposes the relative motion between its adjacent layers. This property of the fluid is known as viscosity. It is also called the resistance of fluid to flow or deformation or fluid thickness.

Effect of temperature on Viscosity:

The viscosity of the fluid decreases sharply with the temperature rise and becomes zero at boiling temperature. On the other hand, the viscosity of the gases increases with the temperature rise.

Definition of Viscous Force (Internal Frictional Force):

When a layer of fluid slide over another layer of the same fluid then an internal tangential frictional force act between them which opposes the relative motion between the layers. This tangential force is called viscous force or internal frictional force.

In the absence of external force, the viscous force would soon bring the fluid to rest.

Factor affecting the viscous force:

There are the following factors that affect the viscous force-

1.) The viscous force is directly proportional to the contact area of the layers. i.e.

$F \propto A \qquad(1)$

Where $A \rightarrow$ The contact area of the layers

2.) The viscous force is directly proportional to the velocity gradient between the layers. i.e.

$F \propto \frac{\Delta v_{x}}{\Delta z} \qquad(2)$

Where $\frac{\Delta v_{x}}{\Delta z} \rightarrow$ The velocity gradient that is shown in the figure below

From equation $(1)$ and equation $(2)$

$F \propto A \: \frac{\Delta v_{x}}{\Delta z}$

$F = \pm \: \eta \: A \: \frac{\Delta v_{x}}{\Delta z} \qquad(3)$

Where

$\eta \rightarrow$ It is a constant and also known as the "coefficient of viscosity" of the fluid.

$ \pm \rightarrow$ It indicates that the viscous force $F$ between two layers of fluid is a mutually interacting force. As shown above in figure (B), A layer that is just above layer $A$ exerts a force in the forward direction while a layer that is just below layer $A$ exerts an equal and opposite force i.e. in the backward direction.

Definition of Coefficient of Viscosity:

If $A=1$ and $\frac{\Delta v_{x}}{\Delta z} = 1$, then from equation $(3)$

$\eta = 1$

So from the above equation,  If the contact area and velocity gradient are units then the viscous force between the fluid is known as the coefficient of velocity.

Dimension of coefficient of viscosity:

$\left[ M L^{-1} T^{-1} \right]$

Unit of coefficient of viscosity:

$Kg-m^{-1}s^{-1}$

Here

$1 \: Kg-m^{-1}s^{-1} = 10\: poise = 1 \: decapoise$

Read More

Brief Description of Liquid Lasers

Brief Description: (Liquid Lasers)

Due to their homogeneous properties and a very high optical cavity of liquids, these are also used as active materials in lasers. Liquid lasers are four-level lasers that use liquids as active material or lasing medium. In these lasers, laser tubes are filled with liquid instead of laser rods as in solid-state lasers or gas in gas lasers. Liquid laser medium has some advantages like very high gain, no cracking for high output power, feasibility of cooling the liquid by circulation, narrow frequency spectrum, etc. In liquid lasers, optical pumping is required for laser action. Optical pumping includes flash tubes, nitrogen lasers, excimer lasers, etc. A rare earth ion dissolved in a solution makes it possible to obtain optically pumped laser action in liquids. The first successful liquid laser was reported by using europium ions ($Eu^{+3}$) in which a sharp and strong laser transition was observed at $6131 A^{\circ}$ wavelength. In this laser, a europium chelate ($EuB_{4}P$) was prepared with benzovlacetate and dissolved in alcohol to give a europium concentration $1.2 \times 10^{19} centers/cm^{3}$. Due to the high absorption coefficient of chelate, it gives rise to pumping problems and their viscosity is so high that circulating motion is not feasible. The best solution to date is the liquid selenium oxychloride ($SeOCl_{2}$) which has a low refractive index, good optical transmission, and a density comparable to glass but it is highly toxic.

To reduce the problem in laser action due to high viscosity and pumping in chelate, the organic dyes are used as the lasing medium in liquid lasers. Dyes are organic substances that absorb in the near ultraviolet, visible, or near-infrared region of the spectrum. When organic dyes are used as a lasing medium. usually, as a liquid solution, in a laser, it is called a dye laser. Examples of some dyes are rhodamine, coumarin, fluorescein, etc. A variety of solvents can be used in dye lasers. Some of the solvents used are water, glycol, ethanol, methanol, hexane, cyclohexane, etc. The lasers using dyes like coumarin, xanthene, quinoline, etc. emit laser radiations in the range of wavelengths $400-500 \: nm, 500-70O \: nm, 400-4300 \: nm$, etc, respectively. These lasers have broad spectral bandwidth and fluorescent spectrum and emission in any region of the visible spectrum can be chosen from a large number of dyes. These lasers produce ultra-short pulses of half-width than with any other lasers. These lasers are the cheapest and one of the most widely tunable lasers in the visible region. Dye lasers Can be used as solid, liquid, and gas lasers but liquid solutions of dyes are convenient as their concentration can be controlled

Read More