Minimum Energy Or Zero Point Energy of a Particle in an one dimensional potential box or Infinite Well

Zero Point Energy of a Particle in an Infinite Well Potential Well:

The normalized wave function or eigenwave function:

$\psi_{n}(x) = \sqrt{\frac{2}{L}} sin \left( \frac{n\pi x}{L} \right)$

The probability density

$| \psi_{n}(x)|^{2} = \frac{2}{L} sin^{2} \left( \frac{n\pi x}{L} \right)$

The energy of a particle in a one-dimensional box or infinite potential well:

$E_{n}=\frac{n^{2}h^{2}}{8 mL^{2}}$

Where $n$ is called the quantum number and $n=1,2,3,4..........$ For $n=0, \psi_{n}(x)=0$ and $| \psi_{n}(x)|^{2}=0$. This shows that for $n=0$ $| \psi_{n}(x)|^{2}=0$ will be zero everywhere in the box which means that the probability of finding the particle inside the box is zero. i.e. particle is not present at all inside the box. Thus $n=0$ is not possible.

If $n\neq 0$ then $E \neq 0$. This means that the minimum energy of the particle in the box will not be zero. The minimum energy value will be obtained for the next lowest value of $n$ i.e. for $n=1$, which is

$E_{1}=\frac{h^{2}}{8 mL^{2}}$

This minimum energy of the particle is often called zero point energy which is finite inside the box. According to classical mechanics, the minimum value $E=0$ is also permissible.

Read More

Bohr's Theory of Hydrogen-Like Atoms

A hydrogen-like atom consists of a very small positively-charged nucleus and an electron revolving in a stable circular orbit around the nucleus.

The radius of electrons in stationary orbits:

Let the charge, mass, velocity of the electron and the radius of the orbit is respectively  $e$, $m$, and $v$  and $r$. The $+ze$ is the positive charge on the nucleus where $Z$ is the atomic number of the atom. As We know that when an electron revolves around the nucleus then the centripetal force on an electron is provided by the electrostatic force of attraction between the nucleus and an electron, we have

$\frac{mv^{2}}{r}=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(e)}{r^{2}}$

$mv^{2}=\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} \qquad(1)$

According to the first postulate of Bohr's model of the atom, the angular momentum of the electron is

$mvr=n \frac{h}{2 \pi} \qquad(2)$

Where $n \: (=1,2,3,.....)$ is quantum number.

Now squaring equation $(2)$ and dividing by equation $(1)$, we get

$r=n^{2} \frac{h^{2} \epsilon_{\circ}}{\pi m Z e^{2}} \qquad(3)$

The above equation is for the radii of the permitted orbits. From the above equation, this concluded that

$r \propto n^{2}$

Since, $n =1,2,3,.....$ it follows that the radii of the permitted orbits increased in the ratio $1:4:9:16:,.....$ from the first orbit.

Bohr's Radius:

For Hydrogen Atom $(z=1)$, The radius of the atom of the first orbit $(n=1)$ will be

$r_{1}= \frac{h^{2} \epsilon_{\circ}}{\pi m e^{2}}$

This is called Bohr's radius and its value is $0.53 A^{\circ}$. Since $r \propto n^{2}$, the radius of the second orbit of the hydrogen atom will be $( 4 \times 0.53 A^{\circ}) $ and that of the third orbit $9 \times 0.53 A^{\circ}$

The velocity of electrons in stationary orbits:

The velocity of the electron in permitted orbits can be obtained by the formula of equation $(2)$

$v=n\frac{h}{2 \pi m r}$

Now put the value of $r$ in above eqaution from equation $(3)$, we get

$v=\frac{Ze^{2}}{2 h \epsilon_{\circ}} \left( \frac{1}{n} \right) \quad(4)$

Thus $v \propto \frac{1}{n}$

This shows that the velocity of the electron is maximum in the lowest orbit $n=1$ and as goes on higher orbits velocity decreases.

For Hydrogen Atom $(z=1)$, The velocity of electron to move in the first orbit $(n=1)$ is

$v_{1}=\frac{e^{2}}{2h\epsilon_{\circ}}$

Its value is $2.19 \times 10^{6} m/sec$

Note:

$\frac{v_{1}}{c}= \frac{2.19 \times 10^{6}}{3 \times 10^{8}} =\frac{1}{137}$

Thus, $\frac{v_{1}}{c}$ or $\frac{e^{2}}{2h\epsilon_{\circ}}$ is a pure number. It is called the "Fine Structure Constant" and is denoted by $\alpha$

The energy of electrons in stationary orbits:

The total energy $E$ of a moving electron in an orbit is the sum of kinetic energies and potential energies. The kinetic energy of moving the electron in a stationary orbit is:

$K=\frac{1}{2} m v^{2}$

Now susbtitute the value of $v$ from equation $(1)$, we get

$K=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$

The potential energy of a moving electron in an orbit of radius $r$ due to the electrostatic attraction between nucleus and electron is given by

$U=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(-e)}{r}$

$U=-\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $

The total energy of the electron is

$E=K+U$

$E=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r} -\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $

$E=-\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$

Subtituting the value of $r$ in above equation from equation $(3)$, we get

$E=-\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n^{2}} \right) \qquad(5)$

This is the equation for the energy of the electron in the $n^{th}$ orbit.

Suppose, Excited state energy is $E_{2}$ and lower state energy is $E_{1}$. So the energy difference between these two states is:

$E_{2}- E_{1}= \frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}} \right) \qquad(6)$

According to the third postulate of Bohr's Atomic model, the frequency $\nu$ of the emitted electromagnetic wave:

$\nu=\frac{E_{2}- E_{1}}{h}$

$\nu=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$

The corresponding wavelength $\lambda$ of the emitted electromagnetic radiation is given by

$\frac{c}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$

$\frac{1}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(7)$

Where $\frac{1}{\lambda}$ is called "wave number" (i.e. number of waves per unit length). In the last equation$(7)$, the quantity $\frac{m e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}}$ is a constant an it is known as "Rydberg Constant (R)". That is

$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \qquad(8)$

So equation $(7)$ can be written as

$\frac{1}{\lambda}=z^{2} R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(9)$

This is Bohr's formula for hydrogen and hydrogen-like atoms $(He^{+}, Li^{++},.......)$.

For hydrogen $Z=1$

$\frac{1}{\lambda}= R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(10)$

The value of the Rydberg Constant is

$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} = 1.090 \times 10^{7} m^{-1}$

This value fairly agrees with empirical value $(1.097 \times 10^{7} m^{-1})$ obtained experimentally by Balmer.

The total energy in terms of Rydberg's Constant:

The $E$ expression can be written in terms of Rydberg's constant $R$ in a simplified form. So from equation $(5)$ and $(8)$ we get

$E=-Z^{2}\frac{Rhc}{n^{2}} \qquad(11)$

Putting the known values of $R$, $h$ and $c$ taking $1 eV =1.6 \times 10^{-19} \: J$ then we get

$E=-Z^{2}\frac{13.6}{n^{2}} \: eV \qquad(12)$

For a Hydrogen atom, $Z=1$

$E=-\frac{13.6}{n^{2}} \: eV \qquad(12)$

Read More

Bohr's Model of Atom

Bohr's Atomic Model Postulates:

Prof Neil in 1913 Bohr solve the difficulties of Ernest Rutherford's atomic model by applying Planck's quantum theory, For this, he proposed the following three Postulates:

1.) Electrons can revolve only in those orbits in which their angular momentum is an integral multiple of $\frac{h}{2 \pi}$. These orbits have discrete energy and definite radii. So it is called the "stable orbits". If the mass of the electron is $m$ and it is revolving with velocity $v$ in an orbit of radius $r$, then its angular momentum will be $mvr$. According to Bohr's postulate,

$mvr=\frac{nh}{2\pi}$

Where $h$ is Planck's universal constant

This Bohr's equation is called the "Bohr's quantization Condition"

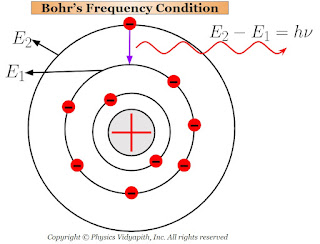
2.) When the electrons revolve in stable orbits then they do not radiate the energy in spite of their acceleration toward the center of the orbit. Hence atom remains stable and is said to exist in a stationary state.

3.) When the atoms receive energy from outside, then one (or more) of their outer electrons leaves their orbit and goes to some higher orbit. These states of the atoms are called the "excited states".

The electrons in the higher orbit stay only for $10^{-8} \: sec$ and return back to anyone lower orbit. While returning back of electrons to lower orbits, they radiate energy in the form of electromagnetic waves.

This radiated energy can be calculated by the energy difference of the electron between the two orbits (i.e. one is higher orbit and the other is lower orbit). If the energy of electron in the higher orbit is $E_{2}$ and that in the lower orbit is $E_{1}$ then net energy difference between the orbits:

$E=E_{2} - E_{1}$

$h \nu=E_{2} - E_{1} \qquad \left( \because E=h\nu \right)$

$\nu=\frac{E_{2} - E_{1}}{h}$

This Bohr's equation is called the "Bohr's frequency condition".

Read More

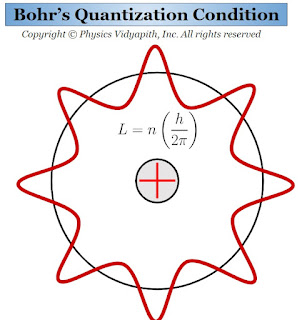
Bohr's Quantization Condition

The Quantization Condition in Bohr Theory of Hydrogen Atom:

$L=\frac{nh}{2 \pi}$

For the angular momentum L, the electron moves arbitrarily only in a stationary circular orbit. According to De Broglie's hypothesis, this condition can be easily obtained. For this purpose, there are following assumptions given below:

1.) The motion of the electron in a stationary circular orbit is represented by a standing matter-wave. If the wavelength of the wave is $\lambda$ then the De Broglie relation

$\lambda=\frac{h}{mv} \qquad(1)$

Where
$m \rightarrow$ The mass of the electron and
$v \rightarrow$ The Velocity in the orbit.

2.) The circular orbit contains an integral number of wavelengths, i.e.

$2 \pi r_{n}= n \lambda $

$\frac{2 \pi r_{n}}{\lambda}= n \qquad(2)$

Where $n=1,2,3............$ and $r_{n}$ is the radius of the orbit.

Substituting the value of $\lambda$ in equation$(2)$

$\frac{2 \pi r_{n} m v}{h} =n$

$mvr_{n} =\frac{nh}{2\pi}$

$L=\frac{nh}{2\pi}$

Which is Bohr's quantization condition.

Read More

Drawbacks of Old Quantum Theory

Planck's quantum hypothesis with its application and extension to explain the black body radiation like the photo-electric effect, the Compton effect, the variation of specific heat of solid with temperature and the spectrum of hydrogen is now called the Old quantum theory. Through these phenomena are successfully explained by the theory, there are numerous drawbacks of the theory. A few of them are as follows.

1.) Bohr's quantization rules are arbitrary. The theory does not provide a physical explanation for the assumptions.

2.) The old quantum theory cannot be applied to explain the spectra of helium and of more complex atoms.

3.) It can provide only a qualitative and incomplete explanation of the intensities of the spectral lines.

4.) It can not explain the dispersion of light.

5.) The theory of non-harmonic vibrations of systems cannot be applied to explain the vibrations of systems.

Read More

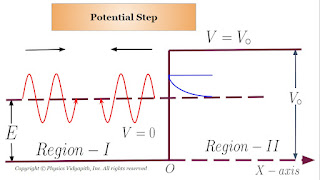
One dimensional Step Potential Barrier for a Particle

Potential Step:

1.) In region $(I)$  i.e.$(-\infty \leq \: x \lt \: 0)$
2.) In region $(II)$ i.e. $(0 \leq \:x \: \leq +\infty)$
Case $(1)$	When $E \lt V_{\circ}$
A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$ B.) Expression for the wave function in the region $(I)$ and $(II)$ C.) Expression for the Probability Current Densities D.) Reflection and Transmission Coefficients
Case $(2)$ :	When $E \gt V_{\circ}$
A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$ B.) Expression for the wave function in the region $(I)$ and $(II)$ C.) Expression for the Probability Current Densities D.) Reflection and Transmission Coefficients

One dimensional step potential barrier for a particle is shown in the figure below.

The meaning of the figure is that the region $(I)$ is at left hand side of the origin $O$ and the potential energy of a particle is zero in this region $(I)$. The region $(II)$ is at the right hand side of $O$ and this region $II$ has constant potential equal to $V_{\circ}$. Such a potential barrier does not exist in nature, but it is approximately similar to the instantaneous potential difference between the dees of a cyclotron or the surface potential barrier of a metal.

Suppose a uniform beam of particles each of mass $m$ and having kinetic energy $E$ is traveling parallel to the x-axis from left to right in the region $(I)$, and is incident on the potential step. In region $(I)$ the energy $E$ of a particle is whole kinetic energy, and in region $(II)$ it is partly kinetic and partly potential energy.

If $E \lt V_{\circ}$, then according to classical mechanics, a particle can enter in the region $(II)$. However according to quantum mechanics although the wave function for an incident particle has a finite value in the region $(II)$ there is no steady transmission of the particle has finite value in this region $(II)$, all the particles are reflected back from the potential step $V_{\circ} \gt E$. In the following discussion, we investigate this behavior of the particles.

Let $\psi_{1}(x)$ and $\psi_{2}(x)$ be the wave function for the motion of a particle in the beam in the region $(I)$ and $(II)$ respectively.

1.) In region $(I)$ i.e. $(-\infty \leq \: x \lt \: 0)$:

According to the time-independent Schrodinger wave equation is:

$-\frac{\hbar^{2}}{2m} \frac{d^{2} \psi_{1}}{dx^{2}}=E \psi_{1}$

$\frac{d^{2} \psi_{1}}{dx^{2}} + \frac{2mE}{\hbar^{2}} \psi_{1} =0$

Let $k_{1}^{2}=\frac{2mE}{\hbar^{2}} $, Now substitute this value in the above equation that can be written as

$\frac{d^{2} \psi_{1}}{dx^{2}} + k_{1}^{2} \psi_{1} =0 \qquad(1)$

2.) In region $(II)$ i.e. $(0 \leq \:x \: \leq +\infty)$:

Case $(1)$ : When $E \lt V_{\circ}$

Then according to the time-independent Schrodinger wave equation for the above case is:

$\frac{d^{2} \psi_{2}}{dx^{2}} + \frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}} \psi_{2} =0$

$\frac{d^{2} \psi_{2}}{dx^{2}} - \frac{2m \left(V_{\circ} -E \right)}{\hbar^{2}} \psi_{2} =0$

Let $\beta^{2}=\frac{2m\left(V_{\circ} -E \right)}{\hbar^{2}} $, Now substitute this value in the above equation that can be written as

$\frac{d^{2} \psi_{2}}{dx^{2}} - \beta^{2} \psi_{2} =0 \qquad(2)$

The general solution of the equation $(1)$ and equation $(2)$ is

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad(3)$

$\psi_{2} (x) = C e^{- \beta \: x} + D e^{\beta \: x} \qquad(4)$

In equation $(3)$ the term $A e^{ik_{1}x}$ represents a wave of amplitude $A$ traveling in the positive x-axis direction and term $B e^{-ik_{1}x} $ is the wave of amplitude $B$ reflected from potential step in the negative x-axis direction. In equation $(4)$ the term $C e^{- \beta \: x}$ is an exponentially decreasing wave function representing a non-oscillatory disturbance that penetrates the potential barrier for some finite distance in the positive x-axis direction and the term $D e^{\beta \: x}$ is an exponentially increasing wave function in the positive x-axis direction. According to the physical interpretation, wave function $\psi$ must remain finite when $x$ approaches $\infty$. From this condition, it follows that $D=0$. Hence in the region $(II)$, the valid solution of the wave equation is:

$\psi_{2} (x) = C e^{- \beta \: x} \qquad(5)$

A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$:

i) At $x=0$, we have

$\psi_{1}(0) = \psi_{2}(0)$

So from equation $(3)$ and equation $(5)$, we have

$A+B=C \qquad(6)$

ii) We also have

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0} = \left( \frac{d\psi_{2}}{dx} \right)_{x=0}$

So again from equation $(3)$ and equation $(5)$, we have

$A\:i\:k_{1} - B\:i\:k_{1} = - C \: \beta$

$A - B = - \frac{C \: \beta}{i\:k_{1} }$

$A - B = \frac{iC \: \beta}{k_{1} } \qquad(7)$

Adding equation $(6)$ and equation $(7)$

$2A = \left( 1 + \frac{ i \beta}{k_{1}} \right)C$

$2A = \left(\frac{k_{1} + i \beta}{k_{1}} \right)C$

$C = \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A \qquad(8)$

Now subtracting the equation $(7)$ from equation $(6)$

$2B = \left( 1 - \frac{ i \beta}{k_{1}} \right)C$

$2B = \left(\frac{k_{1} - i \beta}{k_{1}} \right)C$

Now substitute the value of $C$ from equation $(8)$ in the above equation then we get

$2B = \left(\frac{k_{1} - i \beta}{k_{1}} \right) \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A$

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad(9)$

The equation $(8)$ and equation $(9)$ can be expressed in polar form.

Let $k_{1}= r \: cos\delta$ and $\beta=r\: sin \delta$

Then $r=\sqrt {k_{1}^{2} + \beta^{2}}$ and $tan \delta =\frac{\beta}{k_{1}}$

Now subtitute the value of $k_{1}$ and $\beta$ in equation $(9)$

Now substitute the value of $k_{1}$ and $\beta$ in equation $(9)$

$B = \left(\frac{r \: cos\delta - i r\: sin \delta}{r \: cos\delta + i r\: sin \delta} \right)A $

$B = \left(\frac{ \: cos\delta - i \: sin \delta}{ \: cos\delta + i \: sin \delta} \right)A $

$B = \left(\frac{ e^{-i\delta}}{ e^{i\delta}} \right)A $

$B = e^{-2i \delta} A \qquad(10) $

Now from eqaution $(8)$

$C = \left(\frac{2k_{1} }{k_{1} + i \beta} - 1 + 1 \right)A $

$C = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} +1 \right)A $

Now substitute the value of $k_{1}$ and $\beta$ in equation $(8)$

$C = \left(\frac{r \: cos\delta - i r\: sin \delta}{r \: cos\delta + i r\: sin \delta} +1 \right)A $

$C = \left(\frac{ \: cos\delta - i \: sin \delta}{ \: cos\delta + i \: sin \delta} +1 \right)A $

$C = \left(e^{-2i \delta} +1 \right)A \qquad(11)$

B.) Expression for the wave function in the region $(I)$ and $(II)$:

(i.) In region $(I)$: $x \lt 0$:

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$

Now substitute the value of $B$ in the above equation:

$\psi_{1} (x) = A e^{ik_{1}x} + e^{-2i \delta} A e^{-ik_{1}x} $

$\psi_{1} (x) = A e^{-i \delta} \left( e^{ik_{1}x} e^{i \delta} + e^{-i \delta} A e^{-ik_{1}x} \right) $

$\psi_{1} (x) = 2A e^{-i \delta} \left[ \frac{e^{ik_{1}x} e^{i \delta} + e^{-i \delta} A e^{-ik_{1}x}}{2} \right] $

$\psi_{1} (x) = 2A e^{-i \delta} cos \left(k_{1}x + \delta \right) \qquad(12) $

(ii.) In region $(II)$: $x \gt 0$:

$\psi_{2} (x) = C e^{- \beta \: x} \qquad \left\{ from \: eqaution \: (5) \right\}$

Now substitute the value of $C$ in the above equation:

$\psi_{2} (x) = \left(e^{-2i \delta} +1 \right)A e^{- \beta \: x} $

$\psi_{2} (x) = A e^{-i \delta} \left(e^{-i \delta} +e^{i \delta} \right) e^{- \beta \: x} $

$\psi_{2} (x) = 2A e^{-i \delta} \left( \frac{e^{-i \delta} +e^{i \delta}}{2} \right) e^{- \beta \: x} $

$\psi_{2} (x) = 2A e^{-i \delta} \left( \frac{e^{-i \delta} +e^{i \delta}}{2} \right) e^{- \beta \: x} $

$\psi_{2} (x) = \left( 2A e^{-i \delta} cos \delta \right) e^{- \beta \: x} \qquad(13)$

This shows that the wave function in the region $(II)$ is exponentially damped.

C.) Expression for the Probability Current Densities:

(i.) In region $(I)$:

a.) The probabilty current density $S_{1}$ for the incident beam of particle is given by

$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{i} =(A e^{ik_{1}x})(A e^{ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} e^{ik_{1}x} e^{-ik_{1}x} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} \frac{\hbar k_{1}}{m}$

$S_{i} = | A|^{2} \frac{\hbar k_{1}}{m} \qquad(14)$

b.) The probability current density $S_{r}$ for the reflected beam of particles is given by:

$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{r} =(B e^{-ik_{1}x})(B e^{-ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{r} = | B |^{2} \frac{\hbar k_{1}}{m} \qquad(15)$

Hence the net probability current density in the region $(I)$ is given by

$S=S_{i} - S_{r}$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - | B |^{2} \right) \qquad(16)$

The intensity of waves:

We know that

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad \left\{ From \: equation \: (9) \right\}$

The complex conjugate of this equation is:

$B^{*} = \left(\frac{k_{1} + i \beta}{k_{1} - i \beta} \right)A^{*} $

$BB^{*}=AA^{*}$

$ | B^{2} | = | A^{2}| \qquad(17)$

Hence the net probability current in the region $(I)$ to the left of the region $O$ is zero.

The equation $ | B^{2} | = | A^{2}|$ shows that the intensity of the reflected wave is equal to that of the incident wave, or the number of particles per second passing normally through the unit area of the incident beam is equal to the number of particles per second passing normally through unit area of the reflected beam. Consequently, the incident and reflected probability currents cancel one another.

(ii.) In region $(II)$:

From the relation $ | B^{2} | = | A^{2}|$ we infer that the probability current density in the region $(II)$ to the right of the origin should be zero. However, we can prove this conclusion using the wave function

$\psi_{2}= C e^{-\beta x}$

and its complex conjugate

$\psi^{*}_{2}= C^{*} e^{-\beta x}$

The proof is as follows:

The probability current density in the region $(II)$ for the transmitted beam of the particles is given by

$S_{t}= -\frac{i \hbar}{2m} \left[ \psi^{*}_{2} \frac{\partial \psi_{2}}{\partial x} - \psi_{2} \frac{\partial \psi^{*}_{2}}{\partial x} \right]$

Now Substitute the value of $\psi$ and $\psi^{*}$ in this above equation:

$S_{t}= -\frac{i \hbar}{2m} \left[C^{*} e^{-\beta x} \frac{\partial C e^{-\beta x}}{\partial x} - C e^{-\beta x} \frac{\partial C^{*} e^{-\beta x}}{\partial x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} - CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} - CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[-CC^{*} e^{-2\beta x} (\beta) + CC^{*} e^{-2\beta x} (\beta) \right]$

$S_{t}=0 \qquad(18)$

The probability current density $S_{t}$ for a transmitted beam of particles is zero

D.) Reflection and Transmission Coefficients:

(i.)Reflection Coefficients:

The reflection coefficient $R$ is defined as the ratio of the probability current density $S_{r}$ for the reflected beam of particles to the probability current density $S_{i}$ for the incident beam of particles. Thus it is given by

$R=\frac{S_{r}}{S_{i}}$

$R=\frac{| B |^{2} \frac{\hbar k_{1}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$R=\frac{| B |^{2} }{| A |^{2}} \qquad(19)$

In this case $(V_{\circ} \gt E)$, $ | B^{2} | = | A^{2}|$ Now the above equation $(19)$ can be written as

$R=1 \qquad(20)$

This shows that the reflection of the incident beam, at the potential step is total.

(ii) Transmission Coefficients:

The transmission coefficient $T$ is defined as the ratio of the probability current density $S_{t}$ for the transmitted beam of the particle to the probability current density $S_{i}$ for the incident beam. Thus it is given by

$T=\frac{S_{t}}{S_{i}} \qquad(21)$

In this case: The probability of current densityin region $(II)$ is zero i.e. $S_{t}=0$ then transmission coefficient

$T=0$

So from above equation, we can conclude that the transmission coefficient of the beam of particles is zero.

Conclusions:

From the foregoing discussion, we draw the following inference:

i.) The reflection of the incident beam of particles, at the potential step is total.

ii.) There is no probability of current density anywhere. To the left hand side of the potential step, the incident and the reflected probability of currents density cancel to each other, and to the right ahnd side of the step, probability of currents density is zero.

iii.) To the right of the step the wave function is not zero, but it is exponentially damped. Therefore there is a finite or definite probability of finding the particle in the region $(II)$

If $V_{\circ} \rightarrow \infty$ and $E$ is finite, then

$\beta=\sqrt {\frac{2m \left( V_{\circ} -E \right)}{\hbar^{2}}} \rightarrow \infty $

In this case the wave function in region $(II)$ is $\psi_{2}= C \: e^{-\beta x} \rightarrow 0 $

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A $, and $C = \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A$

$\underset{\beta \rightarrow \infty}{Lim} \:\: \frac{B}{A}=\frac{\frac{k_{1}}{\beta} - i}{\frac{k_{1}}{\beta}+i} = -1$

$\frac{B}{A} =-1$ Or $A+B=0$ $\qquad(22)$

And, $\underset{\beta \rightarrow \infty}{Lim} \:\: \frac{C}{A}=\frac{2k_{1}} {k_{1}+i \beta} = 0$

$C=0 \qquad(23)$

Or

Hence the wave function

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ From \: equation (3) \right\}$

At $x=0$ is

$\psi_{1} (0) = A + B=0 \qquad(24)$

And the wave function $\psi_{2}= C \: e^{-\beta x}$

At $x=0$ is $\psi_{2}=C=0$

The slope of $\psi_{1}$ at $x=0$ is

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0}= ik_{1} \left( A-B \right) = 2 i k_{1} A \qquad(25)$

Thus at a point where the potential suddenly increases from zero to an infinite value the wave function $\psi_{1}$ becomes zero and ts slope suddenly falls from a finite value $2ik_{1}A$ to zero.

In region $(II)$ : $(0 \leq \:x \: \leq +\infty)$:

Case $(2)$ : When $E \gt V_{\circ}$

If $E \gt V_{\circ}$, then the time-independent Schrodinger wave equation is

$\frac{d^{2} \psi_{2}}{dx^{2}} + \frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}} \psi_{2} =0$

Let $k_{2}^{2}=\frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}}$, Now put this value in the above equation which can be written as

$\frac{d^{2} \psi_{2}}{dx^{2}} - k_{2}^{2} \psi_{2} =0 \qquad(26)$

The general solution of the equation $(26)$ is

$\psi_{2} (x) = G e^{ik_{2}x} + H e^{-ik_{1}x} \qquad(27)$

In this equation the term $G e^{ik_{2}x}$ represents a wave traveling from the potential step in the positive x-direction, and the term $H e^{-ik_{1}x}$ a wave traveling in the negative x-direction towards the potential step. Since the particles are incident only from the left of the potential step $H$ must be zero. Hence in the region, $(II)$ the valid solution of the wave equation is

$\psi_{2} (x) = G e^{ik_{2}x} \qquad(28)$

A.) Expression for the Amplitudes $B$ and $G$ in terms of the Amplitude $A$:

i) At $x=0$, we have

$\psi_{1}(0) = \psi_{2}(0)$

So from equation $(3)$ and equation $(28)$, we have

$A+B=G \qquad(29)$

ii) At this condition that the derivative of the wave function is continuous at $x=0$

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0} = \left( \frac{d\psi_{2}}{dx} \right)_{x=0}$

$A \: ik_{1} - B \: ik_{1} =G \: ik_{2} $

$A-B =\frac{k_{2}}{k_{1}}G \qquad(30)$

Adding equation $(29)$ and equation $(30)$, we get

$2A=\left(\frac{k_{1}+k_{2}}{k_{1}}\right) G$

$G=\left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A \qquad(31)$

Subtracting equation $(30)$ and equation $(29)$, we get

$2B=\left(\frac{k_{1} - k_{2}}{k_{1}}\right) G$

Now subtitute the vaue of $G$ from equation $(31)$ to the above equation

$2B=\left(\frac{k_{1} - k_{2}}{k_{1}}\right) \left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A$

$B=\left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right) A \qquad(32)$

B.) Expression for the wave function in region $(I)$ and $(II)$

(i.) In region $(I)$: $x \lt 0$:

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$

$\psi_{1} = A \left[ e^{ik_{1}x} + \left( \frac{k_{1} - k_{2}}{k_{1} +k_{2}} \right) e^{-ik_{1}x} \right] \qquad(33)$

ii.) In region $(II)$: $x \gt 0$:

$\psi_{2} (x) = G e^{ i k_{2} \: x} \qquad \left\{ from \: eqaution \: (28) \right\}$

$\psi_{2} (x) = \left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A e^{ i k_{2} \: x} \qquad (34)$

C.) Expression for the Probability Current Densities:

(i.) In region $(I)$:

a.) The probabilty current density $S_{1}$ for the incident beam of particle is given by

$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{i} =(A e^{ik_{1}x})(A e^{ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} e^{ik_{1}x} e^{-ik_{1}x} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} \frac{\hbar k_{1}}{m}$

$S_{i} = | A |^{2} \frac{\hbar k_{1}}{m} \qquad(35)$

b.) The probability current density $S_{r}$ for the reflected beam of particles is given by:

$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{r} =(B e^{-ik_{1}x})(B e^{-ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{r} = | B |^{2} \frac{\hbar k_{1}}{m} \qquad(36)$

Hence the net probability current density in the region $(I)$ is given by

$S=S_{i} - S_{r}$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - | B |^{2} \right) \qquad(37)$

From equation $(32)$

$|B|^{2}=\left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

Substitute the above equation value in equation $(37)$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - \left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} |A|^{2} \right)$

$S=\frac{\hbar k_{1}}{m} | A |^{2} \left[ 1 - \left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} \right]$

$S=\frac{\hbar k_{1}}{m} |A|^{2} \left[ \frac{4 k_{1} k_{2}}{\left(k_{1} +k_{2} \right)^{2}} \right]$

$S=\frac{4 k_{1} k_{2}}{\left(k_{1} +k_{2}\right)^{2}} \left( \frac{\hbar k_{1}}{m} \right) | A |^{2} \qquad(38)$

(ii.) In region $(II)$:

The probability current density $S_{t}$ for the transmitted beam of particles in region $(II)$ is given by

$S_{t}= \left( G e^{ i k_{2} \: x} \right) \left( G e^{ i k_{2} \: x} \right)^{*} \frac{\hbar k_{2}}{m} $

$S_{t}= \frac{\hbar k_{2}}{m} |G|^{2} \qquad(39)$

From equation $(31)$, we have

$|G|^{2}=\left(\frac{2k_{1}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

So substitute the value of the above equation in equation $(39)$, then we get

$S_{t}= \frac{\hbar k_{2}}{m} \left(\frac{2k_{1}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

$S_{t}= \frac{4k^{2}_{1}}{\left(k_{1} +k_{2}\right)^{2}} \left( \frac{\hbar k_{2}}{m} \right) |A|^{2} \qquad(40)$

The equation $(38)$ and equation $(40)$ shows that $S=S_{t}$. i.e. The net probability density in the direction from left to right in the region $(I)$ is equal to the probability current density in the region $(II)$.

D.) Reflection and Transmission Coefficients:

(i.)Reflection Coefficients:

The reflection coefficient $R$ is defined as the ratio of the probability current density $S_{r}$ for the reflected beam of particles to the probability current density $S_{i}$ for the incident beam of particles. Thus it is given by

$R=\frac{S_{r}}{S_{i}}$

$R=\frac{| B |^{2} \frac{\hbar k_{1}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$R=\frac{| B |^{2} }{| A |^{2}}$

Now using the equation $(32)$ we get

$R=\frac{\left( k_{1} -k_{2} \right)}{\left( k_{1} + k_{2} \right)} \qquad(41)$

(ii) Transmission Coefficients:

The transmission coefficient $T$ is defined as the ratio of the probability current density $S_{t}$ for the transmitted beam of the particle to the probability current density $S_{i}$ for the incident beam. Thus it is given by

$T=\frac{S_{t}}{S_{i}} $

$T=\frac{| G |^{2} \frac{\hbar k_{2}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$T=\frac{| G |^{2} k_{2}}{ | A |^{2} k_{1} }$

Now using equation $(31)$, we get

$T= \frac{k_{2}}{k_{1}} \left( \frac{2 k_{1}}{k_{1} + k_{2}} \right)^{2}$

$T= \frac{k_{2}}{k_{1}} \frac{4 k^{2}_{1}}{\left( k_{1} + k_{2} \right)^{2}} \qquad(42)$

Adding the equation $(41)$ and equation $(42)$ it is easily verified that

$R+T=1 \qquad(43)$

Read More

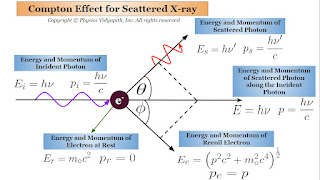
Description of Compton Effect : Experiment Setup, Theory, Theoretical Expression, Limitation, Recoil Electron

The Compton Effect

1	Compton Experiment Setup
2	Theory of the Compton Effect
3	Theoretical Derivation of Compton Effect (Equation of Compton Shift)
4	Limitation of Compton Effect
5	Compton Recoil Electron- 5(a)Relation between $\theta$ and $\phi$ 5(b) Kinetic Energy of the Recoil Electron

1.) Compton Experiment Setup:

The Compton effect is used to verify the particle nature of matter by applying the photoelectric effect. The setup of the Compton experiment as shown in the figure below which consists of the following parts

i.) X-ray source

ii.) Collimator

iii.) Target

iv.) Bragg's Spectrometer

i.) X-ray Source: The X-ray source is used to produce the monochromatic X-ray

ii.) Collimators: The collimators consist of slits that are used to pass the photon in the same direction.

iii.) Target: The target is made up of low atomic number material (i.e. Beryllium, Graphite, Aluminium) in which the monochromatic x-ray is incident and scattered in all directions.

iv.) Braggs Spectrometer: The Braggs spectrometer is used to measure the intensity of these scattered photons of monochromatic X-ray at different angles by the analyzing crystal and ionization chamber.

Working:

When the monochromatic X-ray is produced through an X-ray source and this monochromatic X-ray passes through slit $S_{1}$ and $S_{2}$ (i.e. Collimator). This slit $S_{1}$ and $S_{2}$ passes only the photon of a monochromatic X-ray beam in one direction. Now this beam is incident on graphite block (i.e. Target) and scattered in all directions. Now the intensity of the scattered beam at different angles is measured by a Braggs spectrometer. The major measured intensity by the Braggs spectrometer at different angles is shown in the figure below.

2.) Theory of the Compton Effect:

To explain the effect, Compton applied Einstein's quantum theory of light with the assumption that incident photons possess momentum. The postulates on which the theory is based are as follows.

i.) A beam of monochromatic X-ray is consist of a stream of photons having energy $h\nu$ and momentum $\frac{h\nu}{c}$. These photons travel in the direction of the beam with the speed of light.

ii.) The scattering of X-rays by atoms of graphite element is the result of elastic collisions between photons and electrons. This is an elastic collision so the energy and momentum will be conserved (i.e. in such a collision there is no loss of kinetic energy).

Note: The outer shell electron is loosely bound with the atom and required a very small amount of energy to leave the atom but the X-ray photons have very high energy. So the loosely bound electron of the atom leaves atom the permanently. Therefore for the X-ray loosely bound electrons can be considered as free electrons at rest.

3.) Theoretical Derivation of Compton Effect (Equation of Compton Shift):

Let us consider

The energy of the incident photon $E_{i}=h\nu$

The momentum of the incident photon $p_{i}=\frac{h\nu}{c}$

The energy of the scattered photon $E_{s}=h\nu'$

The momentum of the scattered photon $p_{s}=\frac{h\nu'}{c}$

The relativistic energy of the recoil electron $E_{e}=\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2}$

The momentum of the recoil electron $p_{e}=p$

The energy of an electron at rest $E_{r}=m_{\circ}c^{2}$

The momentum of an electron at rest $p_{r}=0$

According to the energy conservation principle,

The total energy of an electron and an X-ray photon before the collision = The total energy of an electron and an X-ray photon after the collision

$E_{i}+E_{r}= E_{e}+E_{s}$

$h\nu + m_{\circ}c^{2} = \left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} + h\nu'$

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} = h\nu - h\nu' + m_{\circ}c^{2}$

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} = h \left( \nu - \nu' \right) + m_{\circ}c^{2}$

Square the above equation

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right) = \left[ h \left( \nu - \nu' \right) + m_{\circ}c^{2} \right]^{2}$

$p^{2}c^{2} + m_{\circ}^{2}c^{4} = h^{2} \left( \nu - \nu' \right)^{2} + m_{\circ}^{2}c^{4} + 2 h \left( \nu - \nu' \right) m_{\circ}c^{2}$

$p^{2}c^{2} = h^{2} \left( \nu - \nu' \right)^{2} + 2 h \left( \nu - \nu' \right) m_{\circ}c^{2}$

$\frac{p^{2}c^{2}}{h^{2}} = \left( \nu - \nu' \right)^{2} + \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) \qquad(1)$

Momentum is a vector quantity and it is conserved for elastic collision in each of two mutually perpendicular directions.

Total momentum along the direction of the incident photon:

$p\: cos\phi + \frac{h\nu'}{c} \: cos\theta=\frac{h\nu}{c}$

$p\: cos\phi =\frac{h\nu}{c} - \frac{h\nu'}{c} \: cos\theta$

$\frac{pc}{h}\: cos\phi =\nu - \nu'\: cos\theta \qquad(2)$

Total momentum at the right angle to the direction of the incident photon:

$p\:sin\phi=\frac{h\nu'}{c}sin\theta$

$\frac{pc}{h}\: sin\phi =\nu'\: sin\theta \qquad(3)$

To eliminate $\phi$, square the equation $(2)$ and equation $(3)$ and then add them. This gives

$\frac{p^{2}c^{2}}{h^{2}}\: cos^{2}\phi + \frac{p^{2}c^{2}}{h^{2}}\: sin^{2}\phi = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} \left(sin^{2}\phi + cos^{2}\phi \right) = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2}\: cos^{2}\theta - 2 \nu \nu' \:cos\theta + \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} \left(sin^{2}\theta + cos^{2}\theta \right) - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} - 2 \nu \nu'+ 2 \nu \nu' - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu' \right)^{2} + 2 \nu \nu' - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu' \right)^{2} + 2 \nu \nu'\left(1 - cos\theta \right) \quad(4) $

Equation $(1)$ and equation $(4)$ left-hand sides are equal, So equate their right-hand sides, then we get

$ \left( \nu - \nu' \right)^{2} + \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) = \left(\nu - \nu' \right)^{2} + 2 \nu \nu'\left(1 - cos\theta \right)$

$ \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) = 2 \nu \nu'\left(1 - cos\theta \right)$

$ \frac{\left( \nu - \nu' \right)}{\nu\nu'} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right)$

$ \frac{1}{\nu'}-\frac{1}{\nu} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right) \qquad(5)$

$ \frac{c}{\nu'}-\frac{c}{\nu} = \frac{hc}{m_{\circ}c^{2}} \left(1 - cos\theta \right)$

$ \frac{c}{\nu'}-\frac{c}{\nu} = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right)$

$ \lambda'-\lambda = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right) $

$ \Delta \lambda = \lambda'-\lambda = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right) \qquad(6)$

$ \Delta \lambda = \lambda'-\lambda = \frac{2h}{m_{\circ}c} cos^{2}\theta \qquad(7)$

Here the equation $(6)$ and equation $(7)$ is the expression for the Compton Shift in the wavelength of the X-rays, scattered by electrons in a low atomic number material.

The quantity $\frac{h}{2m_{\circ}c}$ is called the "Compton wavelength" of the electron and denoted by $\lambda_{e}$. The numerical value of $\frac{h}{2m_{\circ}c}$ is $0.2426 \times 10^{-11}$ or $0.02426 A^{\circ}$. Now substitute this value in the above equation $(6)$ and equation $(7)$. Therefore

$ \Delta \lambda = \lambda'-\lambda = \lambda_{e} \left(1 - cos\theta \right) \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 0.02426 \left(1 - cos\theta \right) \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 2 \lambda_{e} \: cos^{2}\theta \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 0.04852 \: cos^{2}\theta \: A^{\circ}$

Thus, this theoretical expression derived by Compton is in excellent agreement with this experimental result.

The expression $\Delta \lambda$ leads to the following conclusion:

i.) The wavelength of the radiation scattered at different angles $\theta$ is always greater than the wavelength of the incident radiation.

ii.) The wavelength shifts $\Delta \lambda$ is independent of the wavelength of the incident X-ray, and at a fixed angle of scattering it is the same for all substances containing unbound electrons at rest.

iii.) The wavelength shift increases with the angle of scattering $\theta$ and it has a maximum value equal to $\frac{2h}{m_{\circ}c}$ when $\theta=180^{\circ}$.

4.) Limitation of Compton Effect:

i.) The Compton theory does not explain the presence of X-rays of the same wavelength in the scattered radiation, as the incident rays.

An explanation for this unmodified scattered radiation is as follows:

The incident X-ray photons collide with loosely bound outer electrons and also with tightly bound inner electrons of the atm. During a collision of a photon with tightly bound electrons, the electron is not detached from the atom. Consequently the entire atom recoils. In such a collision the Compton shift of the wavelength is given by replacing $m_{\circ}$ by the mass of the atom in equation $(7)$. Calculations show that this shift is so small that it can not be detected because the mass of an atom is usually several thousand times greater than the mass of the electron at rest.

For Example, The Graphite scattered the mass $M$ of the atom is

$M=12 \times 1840 \times m_{\circ}$

The maximum value of the Compton shift due to the collision of photons with bound electrons of graphite atoms is

$\Delta \lambda = \frac{2h}{Mc} \: sin^{2} \frac{\theta}{2}$

$\Delta \lambda = \frac{2}{12 \times 1840} \left( \frac{h}{m_{\circ}c} \right) \: sin^{2} \frac{180^{\circ}}{2}$

$\Delta \lambda = 9.058 \times 10^{-5} \times 0.02426 A^{\circ}$

$\Delta \lambda = 2.197 \times 10^{-6} A^{\circ}$

Thus the $\Delta \lambda$ is negligible.

ii.) It has been observed that the intensity of the modified X-rays is greater than that of unmodified X-rays for low atomic number materials. But for heavier materials i.e. high atomic number materials the reverse observation has been obtained. These results are not explained by the Compton theory.

5.) Compton Recoil Electron:

To study the direction $\phi$ of ejection of the recoil electron and its energy we derive the following expression

5(a) Relation between $\theta$ and $\phi$:

From the Compton theory, from equation $(5)$ we have

$ \frac{1}{\nu'}-\frac{1}{\nu} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right) $

$ \frac{\nu}{\nu'}-1 = \frac{h \nu}{m_{\circ}c^{2}} \left(1 - cos\theta \right) $

Let $\alpha =\frac{h \nu}{m_{\circ}c^{2}}$, then above equation can be written as

$ \frac{\nu}{\nu'}-1 = \alpha \left(1 - cos\theta \right) $

$ \frac{\nu}{\nu'} = 1 + \alpha \left(1 - cos\theta \right) \qquad(8) $

Now from equation $(2)$ and equation $(3)$

$\frac{pc}{h}\: cos\phi =\nu - \nu'\: cos\theta$

$\frac{pc}{h}\: sin\phi =\nu'\: sin\theta $

Now divide the above equation:

$cot\phi = \frac{\nu - \nu'\: cos\theta}{\nu'\: sin\theta}$

$cot\phi = \frac{1}{sin \theta} \left ( \frac{\nu}{\nu'} - cos \theta \right)$

Now substitute the value $\frac{\nu}{\nu'}$ form equation $(8)$ in above equation

$cot\phi = \frac{1}{sin \theta} \left[ 1 + \alpha \left(1 - cos\theta \right) - cos \theta \right]$

$cot\phi = \frac{\left( 1 + \alpha \right) \left( 1 - cos\theta \right)}{sin \theta}$

$cot\phi = \frac{\left( 1 + \alpha \right) \left( 2 sin^{2}\frac{\theta}{2} \right)}{2 sin \frac{\theta}{2} cos\frac{\theta}{2}} $

$cot\phi = \frac{\left( 1 + \alpha \right) \left( sin\frac{\theta}{2} \right)}{cos\frac{\theta}{2}} $

$cot\phi = \left( 1 + \alpha \right) tan\frac{\theta}{2} \qquad(9)$

This equation shows that the maximum value of $\phi=90^{\circ}$, when $\theta=0^{\circ}$. Therefore, the recoil electrons ejected at angles $\phi$ less than $90^{\circ}$.

5(b) Kinetic Energy of the Recoil Electron:

The kinetic energy of recoil electron $(E)$ is the difference between the kinetic energy of incident photon $(h\nu)$ and the kinetic energy of the scattered photon $(h\nu')$. i.e

$E=h\nu-h\nu' \qquad(10)$

Now from equation $(8)$

$ \frac{\nu}{\nu'} = 1 + \alpha \left(1 - cos\theta \right) $

$ \nu' = \frac{\nu}{1 + \alpha \left(1 - cos\theta \right)} $

Now subtitute the value of $\nu'$ in equation $(10)$, so we get

$E=h\nu-\frac{h \nu}{1 + \alpha \left(1 - cos\theta \right)}$

$E=h\nu \left[1-\frac{1}{1 + \alpha \left(1 - cos\theta \right)} \right]$

$E=h\nu \left[\frac{1 + \alpha \left(1 - cos\theta \right) -1}{1 + \alpha \left(1 - cos\theta \right)} \right]$

$E=h\nu \left[\frac{\alpha \left(1 - cos\theta \right)}{1 + \alpha \left(1 - cos\theta \right)} \right] \qquad(11)$

$E=h\nu \left[\frac{\alpha \left(2sin^{2}\frac{\theta}{2} \right)}{1 + \alpha \left(2sin^{2}\frac{\theta}{2} \right)} \right]$

$E=h\nu \left[\frac{2\alpha}{cosec^{2} \frac{\theta}{2} +2 \alpha} \right] \qquad(12)$

The right-hand side of the above equation can be expressed in terms of $\phi$. Now from equation $(9)$

$cot\phi = \left( 1 + \alpha \right) tan\frac{\theta}{2}$

$\frac{1}{tan \phi}= \left( 1 + \alpha \right) \frac{1}{cot \frac{\theta}{2}}$

$cot \frac{\theta}{2}= \left( 1 + \alpha \right) \: tan \phi $

Now squaring the above equation

$cot^{2} \frac{\theta}{2}= \left( 1 + \alpha \right)^{2} \: tan^{2} \phi $

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} \left( sec^{2}\phi -1 \right) $

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \left( 1 + \alpha \right)^{2}$

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \left( 1 + \alpha^{2}+ 2\alpha \right)$

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - 1 - \alpha^{2} - 2\alpha $

$cosec^{2} \frac{\theta}{2} + 2\alpha = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \alpha^{2} $

Now substitute the value of the above equation in equation $(12)$, then we get

$E=h\nu \left[\frac{2\alpha}{\left( 1 + \alpha \right)^{2} sec^{2}\phi - \alpha^{2}} \right] $

$E=h\nu \left[\frac{2\alpha \: cos^{2}\phi}{\left( 1 + \alpha \right)^{2} - \alpha^{2} \: cos^{2}\phi} \right] $

The experimental value of $E$ of recoil electrons determined by Compton and Simon in $1925$ and by Bless in $1927$ agreed well with the theoretical value.

The study of the Compton effect leads to the conclusion that radiant energy in its interaction with matter behaves as a stream of discrete particles (Photons) each having energy $h\nu$ and momentum $\frac{h\nu}{c}$. In other words, radiant energy is quantized. Therefore the Compton effect is considered a decisive phenomenon in support of the quantization of energy.

Read More

Inadequacy of classical mechanics

Classical mechanics is a branch of physics that deals with the motion of macroscopic bodies or objects $(i.e \: the \: size \: range \: greater \: then \: 10^{-8}m)$ under the influence of forces. While it was groundbreaking when first developed by Sir Isaac Newton in the 17th century, it has certain limitations that were discovered over time. In this answer, we will discuss these limitations in more detail:

1. Classical Mechanics is not applicable to extremely small objects: Classical mechanics assumes that particles have a definite position and momentum, which is not true in the quantum world. This limitation became apparent in the early 20th century with the discovery of quantum mechanics. Quantum mechanics is a branch of physics that deals with the behavior or motion of particles on an atomic and subatomic level $(i.e \: the \: size \: range \: is \: in \: between \: 10^{-8}m \: to \: 10^{-15}m)$ i.e microscopic particles. It has been successful in explaining phenomena such as the photoelectric effect, blackbody radiation, and the behavior of electrons in atoms, which cannot be explained by classical mechanics.
2. Classical Mechanics is not applicable to objects moving at very high speeds: Classical mechanics assumes that the speed of an object can be infinite,  it is not true in the relativistic world. The theory of relativity which was developed by Albert Einstein in the early 20th century, explains the behavior of objects moving at high speeds (i.e. equal to the speed of light). The theory of relativity has been successful in predicting phenomena such as time dilation, length contraction, and the equivalence of mass and energy.
3. Classical Mechanics can not well explain the behavior of systems with many particles: Classical mechanics is not well suited for dealing with systems that have many particles. This is because it is difficult to solve the equations of motion for systems with many particles, and the behavior of the system can become chaotic. The theory of statistical mechanics, developed in the late 19th century, addresses this limitation by using probability distributions to describe the behavior of large systems.
4. Classical Mechanics can not explain the behavior of objects that are very far apart or have very high masses: Newton's law of gravity works well for objects that are close together, but it fails to explain the behavior of objects that are extremely far apart or have very high masses, such as black holes and galaxies. The theory of general relativity, developed by Einstein in the early 20th century, provides a better explanation of the behavior of objects with very high masses and gravitational fields.
5. Classical Mechanics assumes determinism: Classical mechanics assumes that the universe is deterministic, meaning that the future state of a system can be predicted with complete accuracy if the initial state is known. However, this assumption has been challenged by the theory of chaos, which suggests that small changes in the initial state of a system can lead to unpredictable and chaotic behavior in the future.

In summary, while classical mechanics is still useful for understanding the behavior of macroscopic objects, its limitations have led to the development of new theories, such as quantum mechanics, relativity, statistical mechanics, and chaos theory, which can explain the behavior of the universe at different scales and levels of complexity.

Read More

Intensity of a wave

Definition of Intensity of a wave:

In a medium, the energy per unit area per unit time delivered perpendicuar to the direction of the wave propagation s caled the intensity of the wave. It is denoted by $I$.

If the energy $E$ is delivered in the time $t$ rom area $A$ perpendicular to the wave propagation, then

$I=\frac{E}{At} \qquad{1}$

Unit: $Joule/m^{2}-sec$ or $watt/m^{2}$

Dimensional formula: $[MT^{-3}]$

We know that the total mechanical energy of a vibrating particle is

$E=\frac{1}{2}m \omega^{2} a^{2}$

Where $\omega$ is the angular frequency and $a$ is the amplitude of the wave.

$E=\frac{1}{2}m (2\pi n)^{2} a^{2} \qquad \left( \omega=2\pi n \right)$

$E=2 \pi^{2} m n^{2} a^{2} \qquad(2)$

Where $m$ is the mass of the vibrating particle.

Now substitute the value of $E$ from equation $(2)$ to equation $(1)$. So the intensity of the wave

$I=\frac{2 \pi^{2} m n^{2} a^{2}}{At} \qquad(3)$

If the wave travels the distance $x$ in time $t$ with velocity $v$, Then

$t=\frac{x}{v}$

Now substitute the value of the above equation in equation $(3)$

$I=\frac{2 \pi^{2} m v n^{2} a^{2}}{Ax}$

$I=\frac{2 \pi^{2} m v n^{2} a^{2}}{V}$

Where $V$ is the volume of the corresponding medium during the wave propagation in time $t$.

$I=2 \pi^{2} \rho v n^{2} a^{2} \qquad \left(\because \rho=\frac{m}{V} \right)$

It is clear that for wave propagation in a medium with a constant velocity, i.e. wave's intensity is directly proportional to the square of amplitude and frequency both.

$I\propto a^{2}$ and $I \propto n^{2}$

Read More

Difference between sound waves and light waves

Sound Waves:

Sound waves are mechanical waves in nature.

They need a medium to propagate and so cannot be produced in a vacuum.

They can move in all types of mediums as solid liquid or gas whether they are transparent or not.

They propagate in the form of longitudinal waves.

The particle of the medium vibrates along the direction of the propagation and so contraction and rarefaction are formed there.

These are three-dimensional waves.

These waves do not show a polarization effect.

For a normal human being the audible frequency range is $20$ to $20000 Hertz$.

The speed of the sound waves is more in a dense medium than in a rare medium.

Light waves:

light waves are electromagnetic waves in nature.

They don't need any medium and so can produce and propagate in a vacuum.

Their velocity in a vacuum is the maximum of value $3 \times 10^{8} m/s$

They can move in a transparent medium only.

They propagate in the form of transverse waves.

The electric field and magnetic field vibration are perpendicular to the direction of wave propagation.

These wave waves are also three-dimensional waves.

These waves source the polarization effect.

For a normal human being the visible frequency range is $4 \times 10^{18} Hz$ to $8 \times 10^{14} Hz$.

The speed of light is more in rare mediums than in dense ones.

Read More