Normalization of the wave function of a particle in one dimension box or infinite potential well

Description of Normalization of the wave function of a particle in one dimension box or infinite potential well:

We know that the wave function for the motion of the particle along the x-axis is

$\psi_{n}(x)= A \: sin \left( \frac{n \pi x}{L} \right) \quad \left\{ Region \quad 0 \lt x \lt a \right\}$

$\psi_{n}(x)= 0 \quad \left\{ Region \quad 0 \gt x \gt a \right\}$

The total probability that the particle is somewhere in the box must be unity. Therefore,

$\int_{0}^{L} \left| \psi_{n}(x)\right|^{2}dx =1$

Now substitute the value of the wave function in the above equation. Then

$\int_{0}^{L} \left| A \: sin \left( \frac{n \pi x}{L} \right) \right|^{2}dx =1$

$\int_{0}^{L} A^{2} \: sin^{2} \left( \frac{n \pi x}{L} \right) dx =1$

$ \frac{A^{2}}{2}\int_{0}^{L} \left[ 1- cos \left( \frac{2n \pi x}{L} \right) \right] dx =1$

$ \frac{A^{2}}{2} \left[ x - \left( \frac{L}{2n\pi} \right) sin \left( \frac{2n \pi x}{L} \right) \right]_{0}^{L} =1$

$ \frac{A^{2}}{2} \left[ L - \left( \frac{L}{2n\pi} \right) sin \left( \frac{2n \pi L}{L} \right) \right] =1$

$ \frac{A^{2}}{2} \left[ L - \left( \frac{L}{2n\pi} \right) sin \left( 2n \pi \right) \right] =1$

$ \frac{A^{2}}{2} \left[ L - \left( \frac{L}{2n\pi} \right) sin \left( 2n \pi \right) \right] =1$

$ \frac{A^{2}}{2} \left[ L - 0 \right] =1 \qquad(\because sin2n\pi =0)$

$ \frac{A^{2} L}{2} =1$

$ A= \sqrt{\frac{2}{L}}$

Hence, the normalized wave function

$\psi_{n}(x)=\sqrt{\frac{2}{L}} sin \left( \frac{n \pi x}{L} \right)$

The absolute square $\left| \psi_{n}(x) \right|^{2}$ of the wave function $\psi_{n}(x)$ gives the probability density. Hence

$\left| \psi_{n}(x) \right|^{2} = \frac{2}{L} sin^{2} \left( \frac{n \pi x}{L} \right)$

The wave function for the particle in a box can be viewed in analogy with standing waves on a string. The wave function for a standing wave that has nodes at endpoints is of the form $\psi_{n}(x)= A \: sin \left( \frac{n \pi x}{L} \right)$. The condition for a standing wave can also be expressed in terms of wavelength.

$\lambda_{n}=\frac{2 \pi}{k_{n}}$

$\lambda_{n}=\frac{2 \pi}{\frac{n \pi}{L}} \qquad \left( \because k_{n}=\frac{n \pi}{L} \right)$

$\lambda_{n}=\frac{2 L}{n}$

$L= \frac{n \: \lambda_{n}}{2}$

So,

$L= \frac{\: \lambda_{1}}{2} \qquad \left( for \: n=1 \right)$

$L= \lambda_{2} \qquad \left( for \: n=2 \right)$

$L= \frac{3 \: \lambda_{3}}{2} \qquad \left( for \: n=3 \right)$

$L= 2 \lambda_{4} \qquad \left( for \: n=4 \right)$

Geo structure of wave function $\psi_{n}(x)$ and wave function's density $\left| \psi_{n}(x) \right|^{2}$.

Variation of the wave function and probability of finding the particle in a one-dimensional box:

We know that normalised wave function $\psi_{n}(x)$

$\psi_{n}(x)=\sqrt{\frac{2}{L}} sin \left( \frac{n \pi x}{L} \right)$

The probability density of wave function $\left| \psi_{n}(x) \right|$

$\left| \psi_{n}(x) \right|^{2} = \frac{2}{L} sin^{2} \left( \frac{n \pi x}{L} \right)$

Maximum Condition:

The values of $\psi_{n}(x)$ and $\left| \psi_{n}(x) \right|^{2}$ will be maximum. When

$sin \left( \frac{n \pi x}{L} \right)=1$

$sin \left( \frac{n \pi x}{L} \right )=sin \frac{\left( 2m+1 \right) \pi}{2}$

$ \frac{n \pi x}{L} =\left( 2m+1 \right) \frac{ \pi}{2}$

$ x =\left( 2m+1 \right) \frac{ L}{2n}$

Minima Condition:

The values of $\psi_{n}(x)$ and $\left| \psi_{n}(x) \right|^{2}$ will be minima. When

$sin \left( \frac{n \pi x}{L} \right)=0$

$sin \left( \frac{n \pi x}{L} \right)= \sin \: m\pi$

$ \frac{n \pi x}{L} = \: m\pi$

$x=m\left( \frac{L}{n} \right)$

Read More

The electric potential energy of an electric dipole in the uniform electric field

Derivation of the electric potential energy of an electric dipole in the uniform electric field:

Let us consider an electric dipole $AB$, which is made up of two charges $q_1$ and $q_2$, which are placed at a distance of $2l$ in the electric field $E$. So force acting on each charge due to the electric field will be $qE$. If the dipole gets rotated a small-angle $d\theta$ against the torque acting on it in the uniform electric field $E$ then the small work done is

$dW=\tau. d\theta \qquad (1)$

Force of moment on an electric Dipole

The torque (i.e moment of force) on an electric dipole in a uniform electric field

$ \tau=p.E\:sin\theta$

Now substitute the value of $\tau$ in equation $(1)$. So work done

$ dW=p.E\:sin\theta.d\theta$

If the dipole rotate the angle from $\theta_{1}$ to angle $\theta_{2}$ then workdone

$\int_{W_{1}}^{W_{2}}dW=p.E\int_{\theta_{1}}^{\theta_{2}}sin\theta \: d\theta$

$ W_{2}-W_{1}=p.E\left[-cos\theta \right]_{\theta_{1}}^{\theta_{2}}$

$ \Delta W= p.E \left( cos\theta_{1}-cos\theta_{2} \right)\qquad\qquad (2)$

This work is stored in the form of the electric potential energy of an electric dipole in the electric field. So

$U=\Delta W$

$U=p.E \left( cos\theta_{1}-cos\theta_{2} \right)$

If the electric dipole rotates from $0^{\circ}$ (when the direction of electric dipole moment $p$ is aligned in the direction of the electric field $E$) to an angle $\theta$ in the electric field i.e $\theta_{1}=0^{\circ}$ and $\theta_{2}=\theta$ then the electric potential energy of dipole in a uniform electric field

$U=p.E (1-cos\theta)$

Case-(I) If $\theta=0^{\circ}$ i.e It is stable equilibrium position then

$U_{min}=0$

Case-(II) If $\theta=90^{\circ}$ i.e Position of zero energy then

$U=pE$

Case-(III) If $\theta=180^{\circ}$ i.e It is unstable equilibrium position then

$U_{max}=2pE$

Read More

de-Broglie Concept of Matter wave

Louis de-Broglie thought that similar to the dual nature of light, material particles must also possess the dual character of particle and wave. This means that material particles sometimes behave as particle nature and sometimes behave like a wave nature.

According to de-Broglie –

A moving particle is always associated with a wave, called as de-Broglie matter-wave, whose wavelengths depend upon the mass of the particle and its velocity.

According to Planck’s theory of radiation–

$E=h\nu \qquad(1) $

Where
h – Planck’s constant
$\nu $ - frequency

According to Einstein’s mass-energy relation –

$E=mc^ {2} \qquad (2)$

According to de Broglie's hypothesis equation $ (1)$ and equation $(2)$ can be written as –

$mc^ {2} = h \nu$

$mc^ {2} = \frac{hc}{\lambda }$

$\lambda =\frac{h}{mc}\qquad(3) $

$\lambda =\frac{h}{P}$

Where $P$ –Momentum of Photon

Similarly from equation $(3)$ the expression for matter waves can be written as

$\lambda=\frac{h}{mv}=\frac{h}{P}\qquad(4)$

Here $P$ is the momentum of the moving particle.

1.) de-Broglie Wavelength in terms of Kinetic Energy

$K=\frac{1}{2} mv ^{2}$

$K=\frac{m^{2}v^{2}}{2m}$

$K=\frac{P^{2}}{2m}$

$P=\sqrt{2mK}$

Now substitute the value of $P$ in equation $ (4)$ so

$\lambda =\frac{h}{\sqrt{2mK}} \qquad (5)$

2.) de-Broglie Wavelength for a Charged particle

The kinetic energy of a charged particle is $K = qv$

Now substitute the value of $K$ in equation$(5)$ so

$\lambda =\frac{h}{\sqrt{2mqv}}$

3.) de-Broglie Wavelength for an Electron

The kinetic energy of an electron

$K=ev$

If the relativistic variation of mass with a velocity of the electron is ignored then $m=m_{0}$ wavelength

$\lambda =\frac{h}{\sqrt{2m_{0}ev}}$

So wavelength of de-Broglie wave associated with the electron in non-relativistic cases

4.) de-Broglie wavelength for a particle in Thermal Equilibrium

For a particle of mass $m$ in thermal equilibrium at temperature $T@

$K=\frac{3}{2}kT$

Where $K$ – Boltzmann Constant

$\lambda =\frac{h}{\sqrt{2m.\frac{3}{2}kt}}$

$\lambda =\frac{h}{\sqrt{3mKT}}$

Properties of matter wave →

1. Matter waves are generated only if the material's particles are in motion.


2. Matter-wave is produced whether the particles are charged or uncharged.
3. The velocity of the matter wave is constant; it depends on the velocity of material particles.


4. For the velocity of a given particle, the wavelength of matter waves will be shorter for a particle of large mass and vice-versa.


5. The matter waves are not electromagnetic waves.


6. The speed of matter waves is greater than the speed of light.
   
   
   According to Einstein’s mass-energy relation
   
   
   $E=mc^{2}$
   
   
   $h\nu = mc^{2}$
   
   
   $\nu =\frac{mc^{2}}{h}$
   
   
   Where $\nu$ is the frequency of matter-wave.
   
   
   We know that the velocity of matter-wave
   
   
   $ u =\nu \lambda $
   Substitute the value of $\nu$ in the above equation
   
   
   $u =\frac{mc^{2}}{h}. \lambda $
   $u =\frac{mc^{2}}{h} . \frac{h}{mv}$
   
   

   $u =\frac{c^{2}}{v}$

   
   
   Where $v$ → particle velocity which is less than the velocity of light.


7. The wave and particle nature of moving bodies can never be observed simultaneously.

Read More

Group velocity is equal to particle velocity

Prove that: Group velocity is equal to Particle Velocity

Solution:

We know that group velocity

$V_{g}=\frac{d\omega}{dk}$

$V_{g}=\frac{d(2\pi\nu )}{d(\frac{2\pi }{\lambda })} \qquad \left(k=\frac{2\pi}{\lambda} \right)$

$V_{g}=\frac{d\nu}{d(\frac{1}{\lambda })}$

$\frac{1}{V_{g}}=\frac{d( \frac{1}{\lambda })}{d\nu}\qquad(1)$

We know that the total energy of the particle is equal to the sum of kinetic energy and potential energy. i.e

$E=K+V$

Where

$K$ – kinetic energy
$V$ – Potential energy

$E=\frac{1}{2} mv^{2}+V$

$E-V=\frac{1}{2}\frac{(mv)^2}{m}$

$E-V=\frac{1}{2m }(mv)^2$

$2m(E-V)=(mv)^2$

$mv=\sqrt{2m(E-V)}$

According to de-Broglie wavelength-

$\lambda =\frac{h}{mv}$

$\lambda =\frac{h}{\sqrt{2m(E-V)}}$

$\frac{1}{\lambda} =\frac{\sqrt{2m(E-V)}}{h}\qquad(3)$

Now put the value of $\frac{1}{\lambda }$ in equation$(1)$

$\frac{1}{V_{g}} =\frac{d}{dv}[\frac{{2m(E-V)}^\tfrac{1}{2}}{h}]$

$\frac{1}{V_{g}} =\frac{d}{dv}[\frac{{2m(h\nu -V)}^\tfrac{1}{2}}{h}]$

$\frac{1}{V_{g}} =\frac{1}{2h}[{2m(h\nu -V)}]^{\tfrac{-1}{2}}{2m.h}$

$\frac{1}{V_{g}} =\frac{1}{2h}[{2m(E -V)}]^{\tfrac{-1}{2}}{2m.h} \qquad \left(\because E=h\nu \right) $

$\frac{1}{V_{g}} =\frac{m}{mv}$     {from equation $(2)$}

$V_{g}=V$

Thus, the above equation shows that group velocity is equal to particle velocity.

Read More

Solution of electromagnetic wave equations in conducting media

The electromagnetic wave equations in conducting media:

For electric field vector:

$ \nabla^{2}.\overrightarrow{E}-\mu \epsilon\frac{\partial^{2} \overrightarrow{E}}{\partial t^{2}} - \sigma \mu \frac{\partial \overrightarrow{E}}{\partial t}=0 \qquad(1)$

For magnetic field vector:

$\nabla^{2}.\overrightarrow{B} - \mu \epsilon \frac{\partial^{2} B}{\partial t^{2}}-\sigma \mu \frac{\partial \overrightarrow{B}}{\partial t}=0 \qquad(2)$

The wave equation of electric field vector:

$\overrightarrow{E}(\overrightarrow{r},t)=E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(3)$

The wave equation of magnetic field vector:

$\overrightarrow{B}(\overrightarrow{r},t)=B_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(4)$

Now the solution of electromagnetic wave for electric field vector.

Differentiate with respect to $t$ of equation $(3)$

$\frac{\partial \overrightarrow{E}}{\partial t}=i \omega E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

Again differentiate with respect to $t$ of the above equation:

$\frac{\partial^{2} \overrightarrow{E}}{\partial t^{2}}=i^{2} \omega^{2} E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\frac{\partial^{2} \overrightarrow{E}}{\partial^{2} t}=- \omega^{2} \overrightarrow{E}(\overrightarrow{r},t)$

Now substitute the value of the above equation in equation$(1)$

$\nabla^{2} \overrightarrow{E}=-\omega^{2} \mu \epsilon \overrightarrow{E} - i \omega \mu \sigma \overrightarrow{E}$

$\nabla^{2} \overrightarrow{E}=- \left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right) \overrightarrow{E}$

This is the solution of the electromagnetic wave equation in conducting media for the electric field vector.

Now component form of the above equation:

$(\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} +\frac{\partial^{2}}{\partial z^{2}})(\hat{i}E_{x}+\hat{j}E_{y}+\hat{k}E_{z}) \\ =- \left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right)(\hat{i}E_{x}+\hat{j}E_{y}+\hat{k}E_{z}) \qquad(5)$

If the wave is propagating along $z$ direction. Then for uniform-plane electromagnetic waves-

$\frac{\partial}{\partial x}=\frac{\partial}{\partial y}=0$

$\frac{\partial^{2}}{\partial x^{2}}=\frac{\partial^{2}}{\partial y^{2}}=0$

$E_{z}=0$

Now the equation $(5)$ can be written as:

$\frac{\partial^{2}}{\partial x^{2}} (\hat{i}E_{x}+\hat{j}E_{y}) \\ =- \left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right)(\hat{i}E_{x}+\hat{j}E_{y})$

Now separate the above equation in $x$ and $y$ components so

$\left.\begin{matrix} \frac{\partial^{2} E_{x}}{\partial z^{2}}=- \left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right) E_{x} \\ \frac{\partial^{2}E_{y}}{\partial z^{2}} =- \left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right) E_{y} \end{matrix}\right\} \quad(6)$

The solution of electromagnetic wave for magnetic field vector can find out by following the above method.

Therefore $x$ and $y$ components of the solution of the electromagnetic wave equation for magnetic field vector can be written as. i.e.

$\left.\begin{matrix} \frac{\partial^{2} B_{x}}{\partial z^{2}}=- \left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right) B_{x} \\ \frac{\partial^{2}B_{y}}{\partial z^{2}} =- \left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right) B_{y} \end{matrix}\right\} \quad(7)$

In the solution of electromagnetic wave equation $(6)$ and equation $(7)$. The term $\left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right)$ is equal to $k_{z}^{2}$. It is known as propagation constant $k_{z}$. Then

$k_{z}^{2}=\left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right) \qquad(8)$

The propagation constant is the complex quantity so

$k_{z}=\alpha+i \beta \qquad(9)$

Now from equation $(8)$ and equation $(9)$

$\left(\alpha+i \beta \right)^{2}=\left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right)$

$\alpha^{2} - \beta^{2} +2 i \alpha \beta =\left( \omega^{2} \mu \epsilon + i \omega \mu \sigma \right)$

Now separate the real and imaginary terms:

$Real \: Term \rightarrow \alpha^{2} - \beta^{2} = \omega^{2} \mu \epsilon \quad (10)$

$Imaginary \: Term \rightarrow 2 \alpha \beta = \omega \mu \sigma \quad (11)$

On solving the equation $(10)$ and equation $(11)$

$\alpha= \omega \sqrt{\frac{\mu \epsilon}{2}} \left[ 1 + \left\{ 1+ \left( \frac{\sigma}{\epsilon \omega} \right)^{2} \right\}^{1/2} \right]^{1/2} \quad(12)$

$\beta= \omega \sqrt{\frac{\mu \epsilon}{2}} \left[ \left\{ 1+ \left( \frac{\sigma}{\epsilon \omega} \right)^{2} \right\}^{1/2} -1 \right]^{1/2} \quad(13)$

The wave equation $(3)$ of the electric field vector also can be written as:

$\overrightarrow{E}(\overrightarrow{r},t)=E_{\circ} e^{-\beta \overrightarrow{r}}e^i{(\alpha \overrightarrow{r} - \omega t)} \qquad(14)$

The above equation has an additional term $e^{-\beta \overrightarrow{r}}$ compared to the purely harmonic solution.

Where
$\alpha \rightarrow$ Attenuation Constant
$\beta \rightarrow$ Absorption Coefficient and Phase Constant

Read More

Electromagnetic Wave Equation in Conducting Media (i.e. Lossy dielectric or Partially Conducting)

Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of electrostatic, Gauss's law of magnetism, Faraday's law of electromotive force, and Ampere's Circuital law. Maxwell converted the integral form of these equations into the differential form of the equations. The differential form of these equations is known as Maxwell's equations.

1. $\overrightarrow{\nabla}. \overrightarrow{E}= \frac{\rho}{\epsilon_{0}}$


2. $\overrightarrow{\nabla}. \overrightarrow{B}=0$


3. $\overrightarrow{\nabla} \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}$


4. $\overrightarrow{\nabla} \times \overrightarrow{B}= \mu \overrightarrow{J}$
   
   
   Modified form:
   
   
   $\overrightarrow{\nabla} \times \overrightarrow{B}= \mu \overrightarrow{J}+\mu \epsilon \frac{\partial \overrightarrow{E}}{\partial t}$

For Conducting Media:

Current density $(\overrightarrow{J}) = \sigma \overrightarrow{E} $
Volume charge distribution $(\rho)=0$
Permittivity of Conducting Media= $\epsilon$
Permeability of Conducting Media=$\mu$

Now, Maxwell's equation for Conducting Media:

$\overrightarrow{\nabla}. \overrightarrow{E}=0 \qquad(1)$
$\overrightarrow{\nabla}. \overrightarrow{B}=0 \qquad(2)$
$\overrightarrow{\nabla} \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t} \qquad(3)$
$\overrightarrow{\nabla} \times \overrightarrow{H}= \overrightarrow{J}$

Modified form for Conducting Media:

$\overrightarrow{\nabla} \times \overrightarrow{B}= \mu \overrightarrow{J}+\mu \epsilon \frac{\partial \overrightarrow{E}}{\partial t}$

$\overrightarrow{\nabla} \times \overrightarrow{B}= \mu \sigma \overrightarrow{E}+ \mu \epsilon \frac{\partial \overrightarrow{E}}{\partial t} \qquad(4)$

Now, On solving Maxwell's equation for conducting media i.e perfect dielectric and lossless media, gives the electromagnetic wave equation for conducting media. The electromagnetic wave equation has both an electric field vector and a magnetic field vector. So Maxwell's equation for conducting medium gives two equations for electromagnetic waves i.e. one is for electric field vector($\overrightarrow{E}$) and the second is for magnetic field vector ($\overrightarrow{H}$).

Electromagnetic wave equation for conducting media in terms of $\overrightarrow{E}$:

Now from equation $(3)$

$\overrightarrow{\nabla} \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t} $

Now take the curl on both sides of the above equation$

$\overrightarrow{\nabla} \times (\overrightarrow{\nabla} \times \overrightarrow{E})=-\overrightarrow{\nabla} \times \frac{\partial \overrightarrow{B}}{\partial t} $

$(\overrightarrow{\nabla}. \overrightarrow{E}).\overrightarrow{\nabla} - (\overrightarrow{\nabla}. \overrightarrow{\nabla}).\overrightarrow{E}=-\frac{\partial}{\partial t} (\overrightarrow{\nabla} \times \overrightarrow{B}) \qquad(5)$

We know that

$\overrightarrow{\nabla}. \overrightarrow{E}=0 $
$\overrightarrow{\nabla}.\overrightarrow{\nabla}=\nabla^{2}$
$\overrightarrow{\nabla} \times \overrightarrow{B}=\sigma \mu \overrightarrow{E} + \mu \epsilon \frac{\partial \overrightarrow{E}}{\partial t} $

Now substitute these values in equation $(5)$. So

$ -\nabla^{2}.\overrightarrow{E}=-\frac{\partial}{\partial t} \left(\sigma \mu \overrightarrow{E} + \mu \epsilon \frac{\partial \overrightarrow{E}}{\partial t} \right)$

$ -\nabla^{2}.\overrightarrow{E}=-\mu \frac{\partial}{\partial t} \left(\sigma \overrightarrow{E} + \epsilon \frac{\partial \overrightarrow{E}}{\partial t} \right)$

$ \nabla^{2}.\overrightarrow{E}=\mu \epsilon \frac{\partial^{2} \overrightarrow{E}}{\partial t^{2}} + \sigma \mu \frac{\partial \overrightarrow{E}}{\partial t} $

$ \nabla^{2}.\overrightarrow{E}-\mu \epsilon \frac{\partial^{2} \overrightarrow{E}}{\partial t^{2}} - \sigma \mu \frac{\partial \overrightarrow{E}}{\partial t}=0 $

The value of $\frac{1}{\sqrt{\mu \epsilon}}= v$. Where $v$ is the speed of the electromagnetic wave in the conducting medium. So the above equation is often written as

$ \nabla^{2}.\overrightarrow{E}-\frac{1}{v^{2}}\frac{\partial^{2} \overrightarrow{E}}{\partial t^{2}} - \sigma \mu \frac{\partial \overrightarrow{E}}{\partial t}=0 $

This is an electromagnetic wave equation for conducting media in terms of electric field vector ($\overrightarrow{E}$).

Electromagnetic wave equation for conducting media in terms of $\overrightarrow{B}$:

Now from MAxwell's equation $(4)$

$\overrightarrow{\nabla} \times \overrightarrow{B}= \mu \sigma \overrightarrow{E}+ \mu \epsilon \frac{\partial \overrightarrow{E}}{\partial t}$

Now take the curl on both sides of the above equation

$\overrightarrow{\nabla} \times (\overrightarrow{\nabla} \times \overrightarrow{B})=\overrightarrow{\nabla} \times \left( \mu \sigma \overrightarrow{E}+ \mu \epsilon \frac{\partial \overrightarrow{E}}{\partial t} \right) $

$(\overrightarrow{\nabla}. \overrightarrow{B}).\overrightarrow{\nabla} - (\overrightarrow{\nabla}. \overrightarrow{\nabla}).\overrightarrow{B} \\ =\overrightarrow{\nabla} \times \sigma \mu \overrightarrow{E}+ \mu \epsilon \left( \overrightarrow{\nabla} \times \frac{\partial \overrightarrow{E}}{\partial t} \right)$

$(\overrightarrow{\nabla}. \overrightarrow{B}).\overrightarrow{\nabla} - (\overrightarrow{\nabla}. \overrightarrow{\nabla}).\overrightarrow{B} \\ =\sigma \mu \left( \overrightarrow{\nabla} \times \overrightarrow{E} \right)+ \mu \epsilon \frac{\partial }{\partial t}\left( \overrightarrow{\nabla} \times \overrightarrow{E} \right) \qquad(6)$

We know that

$\overrightarrow{\nabla}. \overrightarrow{B}=0$
$\overrightarrow{\nabla}.\overrightarrow{\nabla}=\nabla^{2}$
$\overrightarrow{\nabla} \times \overrightarrow{E}= -\frac{\partial \overrightarrow{B}}{\partial t}$

Now substitute these values in equation $(6)$. So

$-\nabla^{2}.\overrightarrow{B}=- \sigma \mu \frac{\partial \overrightarrow{B}}{\partial t} - \mu \epsilon \frac{\partial^{2} B}{\partial t^{2}}$

$\nabla^{2}.\overrightarrow{B}= \sigma \mu \frac{\partial \overrightarrow{B}}{\partial t} + \mu \epsilon \frac{\partial^{2} B}{\partial t^{2}} $

$\nabla^{2}.\overrightarrow{B}-\sigma \mu \frac{\partial \overrightarrow{B}}{\partial t} - \mu \epsilon \frac{\partial^{2} B}{\partial t^{2}}=0 $

The value of $\frac{1}{\sqrt{\mu \epsilon}}= v$. Where $v$ is the speed of the electromagnetic wave in the conducting medium. So the above equation is often written as

$\nabla^{2}.\overrightarrow{B} - \frac{1}{v^{2}} \frac{\partial^{2} B}{\partial t^{2}}-\sigma \mu \frac{\partial \overrightarrow{B}}{\partial t}=0 $

This is an electromagnetic wave equation for conducting media in terms of electric field vector ($\overrightarrow{B}$).

Read More

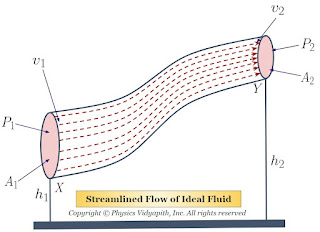
Bernoulli's Theorem and Derivation of Bernoulli's Equation

Statement of Bernoulli's Theorem:

When an ideal fluid (i.e incompressible and non-viscous Liquid or Gas) flows in streamlined motion from one place to another, then the total energy per unit volume (i.e Pressure energy + Kinetic Energy + Potential Energy) at each and every of its path is constant.

$P+\frac{1}{2}\rho v^{2} + \rho gh= constant$

Derivation of Bernoulli's Theorem Equation:

Let us consider that an incompressible and non-viscous liquid is flowing in streamlined motion through a tube $XY$ of the non-uniform cross-section.

Now Consider:

The Area of cross-section $X$ = $A_{1}$
The Area of cross-section $Y$ = $A_{2}$

The velocity per second (i.e. equal to distance) of fluid at cross-section $X$ = $v_{1}$
The velocity per second (i.e. equal to distance) of fluid at cross-section $Y$ = $v_{2}$

The Pressure of fluid at cross-section $X$ = $P_{1}$
The Pressure of fluid at cross-section $Y$ = $P_{2}$

The height of cross-section $X$ from surface = $h_{1}$
The height of cross-section $Y$ from surface = $h_{2}$

The work done per second by force on the liquid Entering the tube at $X$:

$W_{1}$ = Force $ \times $ Distance covered in one second

$W_{1}= P_{1} \times A_{1} \times v_{1} \quad \left( Force =Pressure \times Area \right)$

Similarly
The work done per second by force on the liquid leaving the tube at $Y$:

$W_{2}= P_{2} \times A_{2} \times v_{2}$

The net work done on the liquid:

$\Delta W=W_{1}-W_{2}$
$\Delta W= P_{1} \times A_{1} \times v_{1} - P_{2} \times A_{2} \times v_{2} \qquad(1)$

Now according to the principle of continuity:

$A_{1} v_{1} = A_{2} v_{2} = \frac{m}{\rho} \qquad(2)$

Now from equation $(1)$ and equation $(2)$

$\Delta W=\left( P_{1} -P_{2} \right) \frac {m}{\rho} \qquad(3)$

The kinetic energy of the fluid entering at $X$ in 1 second

$K_{1}=\frac{1}{2}mv_{1}^{2}$

The kinetic energy of the fluid leaving at $Y$ in 1 second

$K_{2}=\frac{1}{2}mv_{2}^{2}$

Therefore, The increase in kinetic energy

$\Delta K = K_{2}-K_{1}$

Now substitute the value of $K_{1}$ and $K_{2}$ in above equation then

$\Delta K = \frac{1}{2}mv_{2}^{2} - \frac{1}{2}mv_{1}^{2}$
$\Delta K = \frac{1}{2}m \left( v_{2}^{2} - v_{1}^{2} \right) \qquad(4)$

The potential energy of fluid at $X$

$U_{1}= mgh_{1}$

The potential energy of fluid at $Y$

$U_{2}= mgh_{2}$

Therefore, The decrease in potential energy

$\Delta U = U_{1}-U_{2}$

Now substitute the value of $U_{1}$ and $U_{2}$ in above equation then

$\Delta U = mgh_{1} - mgh_{2}$
$\Delta U = mg \left( h_{1} - h_{2} \right) \qquad(5)$

This increase in energy is due to the net work done on the fluid, i.e.

Net Work done = Net increase in energy

Net Work done $(\Delta W)$ = Net increase in Kinetic Energy $(\Delta K)$ - Net decrease in Potential Energy $(\Delta U)$

$\left( P_{1} -P_{2} \right) \frac {m}{\rho} = \frac{1}{2}m \left( v_{2}^{2} - v_{1}^{2} \right) - mg \left( h_{1} - h_{2} \right) $

$\left( P_{1} -P_{2} \right) = \frac{1}{2}\rho \left( v_{2}^{2} - v_{1}^{2} \right) -\rho g \left( h_{1} - h_{2} \right) $

$P_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho g h_{1} = P_{2} + \frac{1}{2}\rho v_{2}^{2} + \rho g h_{2} $

$P + \frac{1}{2} \rho v^{2} + \rho g h = Constant $

This is Bernoulli's theorem equation.

Pressure Head, Velocity Head, and Gravitational Head of a Flowing Fluid:

According to Bernoulli's Theorem equation

$P + \frac{1}{2} \rho v^{2} + \rho g h = Constant $

Now dividing the above equation by $\rho g$, then we get

$\frac{P}{\rho g}+\frac{v^{2}}{2g}+ h = Constant$

Where

$\frac{P}{\rho g}$ = Pressure Head

$\frac{v^{2}}{2g}$ = Velocity Head

$h$ = Gravitational Head

The dimension of each of these three is the dimension of height. The sum of these heads is called the 'Total Head'

Therefore, Bernoulli's theorem may also state as follows:

In streamlined motion of an ideal fluid, the sum of pressure head, velocity head and gravitational head at any point is always constant.

When the fluid flows in a horizontal plane $(h_{1}=h_{2})$, then Bernoulli's equation

$P_{1} + \frac{1}{2} \rho v_{1}^{2} = P_{2} + \frac{1}{2}\rho v_{2}^{2} $

$\frac{P}{\rho g}+\frac{v^{2}}{2g} = Constant$

Read More

Numerical Problems and Solutions of Power

Formulas and Solutions to Numerical Problems of Power

Important Formula of Power:

1.) $P=\frac{Work(W)}{Time(t)}$

2.) $P=\frac{F.s}{t}$

3.) $P=\frac{F \: s \: cos \theta}{t}$

4.) $P=\frac{F \: s }{t} \qquad \left( \because \theta =0^{\circ} \right)$

5.) $P=F \: v \qquad \left( \because v = \frac{s}{t} \right)$

Numerical Problems and Solutions

Q.1 A woman pulls a bucket of water of mass $5 Kg$ from a well which is $10 m$ deep in 10 sec. Calculate the power used by her $(g=10 \: m/sec^{2})$.

Solution:
Given that:
The mass of bucket of water $(m)=5 \: Kg$ Depth of well $(h)=10 \: m$

The time taken to pull a bucket from the well $t= 10 \: sec $

The value of gravitational acceleration $g=10 \: m/sec^{2}$

The power used $(P)=?$


Now the power used by her:


$P=\frac{W}{T}$

$P=\frac{mgh}{t} \qquad \left( \because W=mgh \right)$

Now substitute the given values in the equation of power:

$P=\frac{5 \times 10 \times 10}{10}$

$P=50 \: Joule/sec=50 W$

Q.2 A man whose mass is $50 \: Kg$ climbs up $30$ steps of the stairs in $30 \: Sec$. If each step is $20 \: cm$ high, Calculate the power used in climbing the stairs $(g=10 \: m/sec^{2})$

Solution:
Given that:
Mass of a man $(m) = 50 \: Kg$

Climbs up the number of Steps $(N) = 30$

The time is taken to climb up the 30 steps $(t)= 30 \: sec$

The length or height of one step $(l)=20 cm \: = \: 0.20 \: m$

The total length or height of 30 steps $h=30 \times 0.20 \: m$

The power used in climbing the stairs=?

Now, from the equation of power:

$P=\frac{W}{t}$

$P=\frac{mgh}{t} \qquad \left( \because W=mgh \right)$

Now substitute the given values in the above equation:

$P=\frac{50 \times 10 \times 30 \times 0.20 }{30}$

$P=100 \: Joule/sec = 100 \: W$

Q.3 A horse exerts a pull of $300 N$ on a cart so that the horse-cart system moves with a uniform speed of $18 Km/h$ on a level road. Calculate the power in watts developed by the horse and also find its equivalent in horsepower.

Solution:
Given that:
The horse exerts the pull, i.e, force $(F)=300 N$

The unifrm speed of the horse-cart $(v)=18 Km/h$

So the distance moved in $(s)=18 Km=18000m$

The time $(t)=1h= 60 \times 60 sec$

The power developed by the horse$(P)=?$

From the equation of the power, the power developed by a horse in one hour:

$P=\frac{W}{t}$ $P=\frac{F.s}{t}$

Now substitute the given values in the above equation:

$P=\frac{3000 \times 18000}{60 \times 60}$

$P=1500 W$

$P=\frac{1500}{746}$

$P=2 \: hp$

Q.4 A man weighing $60Kg$ climbs up a staircase carrying a load of $20 Kg$ on his head. The staircase has 20 steps, each of height $0.2m$. If he takes $10 sec$ to climb, find his power.

Solution:
Given that:
The weight of man $(m_{1})=60Kg$

The weight of load $(m_{2})=20Kg$

The number of steps in the staircase $(N)=20$

The height of each step $(H)=10s$

The total mass of the man and load $(m)=m_{1}+m_{2}= 60+20=80 Kg$

The total heght of stair case $(h)=N \times H = 20 \times .2= 4 m$



The power of man: $P=\frac{W}{t}$

$P=\frac{mgh}{t}$

$P=\frac{80 \times 9.8 \times 4}{10}$

$P=313.6 W$

Q.5 A car of mass $2000 Kg$ and it is lifted up a distance of $30m$ by a crane in $1 \: min$. A second crane does the same job as the first crane in $2 \: min$. Do both cranes consume the same or different amounts of fuel? Find the power supplied by each crane? Neglecting power dissipation against friction.

Solution:
Given that:
The mass of car $(m)=2000 Kg $

The lifted up distance $(h)=30m$

The time taken by first crane $(t_{1}= 1\: min)$

The time taken by second crane $(t_{2}= 2\: min)$

The work done by each crane:

$W=mgh$

$W=2000 \times 9.8 \times 30$

$W=5.88 \times 10^{5} J$

As both the cranes do the same amount of work, both consume the same amount of fuel.

The power supplied by the first crane:

$P_{1}=\frac{mgh}{t_{1}}$

$P_{1}=\frac{2000 \times 9.8 \times 30}{60}$

$P_{1}=9800 W$

The power supplied by the second crane:

$P_{2}=\frac{2000 \times 9.8 \times 30}{1.2}$

$P_{2}=4900 W$

Q.6 The human heart discharges $75 \: mL$ of blood at every beat against a pressure of $0.1 m$ of Hg. Calculate the power of the heart assuming that the pulse frequency is $80$ beats per minute. Density of $Hg=13.6 \times 10^{3} Kg/m^{3}$.

Solution:
Given that:
The volume of blood discharge per beat $(V)=75 \: mL = 75 \times 10^{-6} m^{-3} $

The pressure of blood $(P)=0.1 m \: of \: Hg$ i.e.

$P= 0.1 \times 13.6 \times 10^{3} N-m^{-2} \quad (\because P=\rho g h)$

The work done per beat $=PV$

The workdone in 80 beats$W =80 \times PV$

The power of heart:

$P=\frac{80 \times PV}{60}$

$P=\frac{80 \times 0.1 \times 13.6 \times 10^{3} \times 75 \times 10^{-6} \times 9.8}{60}$

$P=1.33 W$

Q.7 A machine gun fires $60$ bullets per minute with a velocity of $700 m/sec$. If the mass of each bullet is $50 g$, then find the power developed by the gun.

Solution:
Given that:
The mass of one bullet is $M=50 g$

The number of bullets $N=60$

The mass of $60$ bullets $m=M \times N= 50\times 60 = 300g= 3Kg$

The velocity of the bullet $v=700 m/sec$

The time take to fire $60$ bullets $t=1 \: min = 60 sec$

The power developed by gun:

$P=\frac{W}{t}$

According to the work-energy theorem:

$W=\Delta K$

$P=\frac{\Delta K}{t} $

$P=\frac{m v^{2}}{2t} \quad( \because K=\frac{mv^{2}}{2})$

$P=\frac{3 \times (700)^{2}}{2 \times 60} $

$P=12250 W $

Read More

Variation of Mass with Velocity in Relativity

Derivation of variation of mass with velocity: Consider two systems of reference (frame of reference) $S$ and $S’$. The frame $S’$ is moving with constant velocity $v$ relative to frame $S$.

Let two bodies of masses $m_{1}$ and $m_{2}$ be traveling with velocities $u’$ and $-u’$ parallel to the x-axis in the system $S’$. Suppose the two bodies collide and after collision coalesce into one body.

The principles of conservation of mass and of momentum also hold good in relativity same as in classical mechanics. So now apply the principle of conservation of momentum.

$m_{1}u_{1}+m_{2}u_{2}=\left ( m_{1}+m_{2} \right )v\qquad(1)$

Apply the law of addition of velocities, the velocities $u_{1}$ and $u_{1}$ in the system $S$ corresponding to $u’$ and $-u’$ in frame $S’$ are given by $\rightarrow$

$u_{1}= \frac{u'+v}{1+\frac{u'v}{c^{2}}}\quad or \quad u_{2}= \frac{-u'+v}{1-\frac{u'v}{c^{2}}}\qquad(2)$

Now substitute the value of $u_{1}$ and $u_{1}$ in equation $(1)$

$ m_{1}\frac{u'+v}{\left ( 1+\frac{u'v}{c^{2}} \right )}+m_{2}\frac{-u'+v}{\left ( 1-\frac{u'v}{c^{2}} \right )}=\left ( m_{1}+m_{2} \right )v $

$ m_{1}\left [ \frac{u'+v}{1+\frac{u'v}{c^{2}}}-v \right ]=m_{2}\left [ v- \frac{-u'+v}{1-\frac{u'v}{c^{2}}} \right ]$

$ m_{1}\left [ \frac{u'+v-v-u'\frac{v^{2}}{c^{2}}}{1+u'\frac{v}{c^{2}}} \right ]=m_{2}\left [ \frac{v-u'\frac{v^{2}}{c^{2}}+u'-v}{1- u'\frac{v}{c^{2}}} \right ]$

$ \frac{m_{1}}{m_{2}}= \frac{\left ( 1+u'\frac{v}{c^{2}} \right )}{\left ( 1-u'\frac{v}{c^{2}} \right )}\qquad(3)$

From equation$(2)$

$u_{1}^{2} =\left ( \frac{u'+v}{1+\frac{u'v}{c^{2}}} \right )^{2}$

$ 1-\frac{u_{1}^{2}}{c^{2}}=1- \frac{1}{c^{2}} \left ( \frac{u'+v}{1+\frac{u'v}{c^{2}}} \right )^{2}$

$ 1-\frac{u_{1}^{2}}{c^{2}}= \frac{\left ( 1+\frac{u'v}{c^{2}} \right )^{2}-\left ( \frac{u'+v}{c} \right )^{2}}{\left ( 1+\frac{u'v}{c^{2}} \right )^{2}}$

$ 1-\frac{u_{1}^{2}}{c^{2}}= \frac{\left ( 1-\frac{u'^{2}}{c^{2}} \right )\left ( 1-\frac{v^{2}}{c^{2}} \right )}{\left ( 1+\frac{u'v}{c{2}} \right )}$

$ \left ( 1+\frac{u'v}{c^{2}} \right )^{2}=\frac{\left ( 1-\frac{u'^{2}}{c^{2}} \right )\left ( 1-\frac{v^{2}}{c^{2}} \right )}{1-\frac{u_{1}^{2}}{c^{2}}}$

$ \left ( 1+\frac{u'v}{c^{2}} \right ) =\left [ \frac{\left ( 1-\frac{u'^{2}}{c^{2}} \right )\left ( 1-\frac{v^{2}}{c^{2}} \right )}{1-\frac{u_{1}^{2}}{c^{2}}} \right ]^\frac{1}{2}\qquad(4)$

Similarly, square the velocity of $u_{2}$ and solve the as above, so

$\left ( 1-\frac{u'v}{c^{2}} \right ) =\left [ \frac{\left ( 1-\frac{u'^{2}}{c^{2}} \right )\left ( 1-\frac{v^{2}}{c^{2}} \right )}{1-\frac{u_{2}^{2}}{c^{2}}} \right ]\qquad(5)$

Now substituting the values from equation $(4)$ and equation $(5)$ in equation $(3)$

$\frac{m_{1}}{m_{2}}=\frac{\left ( 1-\frac{u_{2}^{2}}{c^{2}} \right )^{\frac{1}{2}}}{\left ( 1-\frac{u_{1}^{2}}{c^{2}} \right )^{\frac{1}{2}}}$

If the body of mass $m_{2}$ is at rest i.e. $m_{2}=m_{0}$ so velocity of the body in frame-S will be zero. i.e. $u_{2}=0$

Where $m_{0}$ is the rest mass.

$m_{1}=\frac{m_{0}}{\left ( 1-\frac{u_{1}^{2}}{c_{2}} \right )^{\frac{1}{2}}}$

Let $ m_{1}=m$ and $u_{1}=v$ so above equation

$m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$

This is the generalized formula of variation of mass with velocity.

Read More

Galilean Transformation Equations and Failure of Galilean Relativity

What is Transformation Equation?

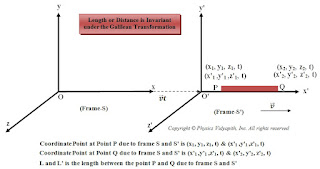
A point or a particle at any instant, in space has different cartesian coordinates in the different reference systems. The equation which provide the relationship between the cartesian coordinates of two reference system are called Transformation equations.

Galilean Transformation Equation:

Let us consider, two frames $S$ and $S'$ in which frame $S'$ is moving with constant velocity $v$ relative to an inertial frame $S$. Let

1. The origin of the two frames coincide at $t=0$


2. The coordinate axes of frame $S'$ are parallel to that of the frame $S$ as shown in the figure below


3. The velocity of the frame $S'$ relative to the frame $S$ is $v$ along x-axis;

The position vector of a particle at any instant $t$ is related by the equation

$ \overrightarrow{r'}=\overrightarrow{r}-\overrightarrow{v}t\qquad (1)$

In component form, the coordinate are related by the equations

$\overrightarrow{x'}=\overrightarrow{x}-\overrightarrow{v}t;\quad y'=y; \quad z'=z\qquad (2)$

The equation $(1)$ and equation $(2)$ express the transformation of coordinates from one inertial frame to another. Hence they are referred to as Galilean transformation.

The equation $(1)$ and equation $(2)$ depending on the relative motion of two frames of reference, but it also depends upon certain assumptions regarding the nature of time and space. It is assumed that the time t is independent of any particular frame of reference. i.e. If $t$ and $t'$ be the times recorded by observers $O$ and $O'$ of an event occurring at $P$ then

$ t=t'\qquad (3)$

Now add the above assumption with transformation equation $(3)$ so the Galilean transformation equations are

$ \begin{Bmatrix} x'=x-vt\\ y'=y\\ z'=z\\ t'=t \end{Bmatrix}\qquad (4)$

The other assumption, regarding the nature of space, is that the distance between two points (or two particles) is independent of any particular frame of reference. For example if a rod has length $L$ in the frame $S$ with the end coordinates $(x_{1}, y_{1}, z_{1})$ and $(x_{2}, y_{2}, z_{2})$ then

$L=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}\quad (5)$

At the same time, the end coordinate of the rod in frame $S'$ are $(x'_{1}, y'_{1}, z'_{1})$ and $(x'_{2}, y'_{2}, z'_{2})$ then

$ L'=\sqrt{(x'_{2}-x'_{1})^{2}+(y'_{2}-y'_{1})^{2}+(z'_{2}-z'_{1})^{2}}\qquad (6)$

But for any time $t$ from equation $(4)$

$ \begin{Bmatrix} x'_{2}-x'_{1}=x_{2}-x_{1}\\ y'_{2}-y'_{1}=y_{2}-y_{1}\\ z'_{2}-z'_{1}=z_{2}-z_{1} \end{Bmatrix}\quad\quad\quad (7)$

So from equation $(5)$, equation $(6)$ and equation $(7)$, we can write as:

$L=L'$

Thus, the length or distance between two points is invariant under Galilean Transformation.

The hypothesis of Galilean Invariance:(Principle of Relativity)

The hypothesis of Galilean invariance is based on experimental observation and is stated as follows:

The basic laws of physics are identical in all reference system which move with uniform velocity with respect to one another.

OR in other words

The basics laws of physics are invariant in inertial frame.

Modify the hypothesis of Galilean Invariance by giving the following statement-

The basic law of physics are invariant in form in two reference system which are connected by Galilean Transformation

Failure of Galilean Relativity OR Galilean Transformation:

There are the following points that could not explain by Galilean transformation:

1. Galilean Transformation failed to explain the actual result of the Michelson-Morley experiment.


2. It violates the postulates of the Special theory of relativity.

According to Maxwell's electromagnetic theory, the speed of light in a vacuum is $c$ $(3\times10^{8} m/sec)$ in all directions. Let us consider a frame of reference relative to which the speed of light is $c$ in all directions, According to Galilean transformation the speed of light in any other inertial system, which is in relative motion with respect to the former, will be different in a different direction. For example- If an observer is moving with speed $v$ opposite or along with the propagation of light, The speed of light $c_{0}$ in the frame of the observer is given by

$ c_{0}=c\:\pm \: v$

Read More