Electric Line of Force and its Properties

Electric Field:

That region around any charged particle (source-charge) in which other test charged particle experience an electric force (attraction or repulsion). This region is called electric field of that charged particle.

The size and magnitude of the test charged particle is very small i.e tends to zero which does not modify the electric field of source charged particle. The electric field can only experience, not be seen by eyes. The electric field is defined by imaginary lines which are called electric field lines.

Electric Field Lines:

Electric field lines are imaginary lines that describe the behavior of electric fields. The behavior of the electric field tells about the force acting on free test-charged particles. This force gives the motion to the free test charge particle which is placed in the path of the electric field line. So the test charged particle moves in the direction of the electric field line. Hence, the direction of electric force and electric field lines both are the same. Thus electric field line is also known as electric lines of force.

Electric Lines of Force:

An electric line of force is defined as an imaginary smooth curve drawn in electric field along which a free isolated test charged particle moves. The tangent drawn at any point on the electric line of force gives the direction of the force acting on a test charged particle placed at that point.

Properties of Electric Line of Force:

There are the following properties of the electric line of force:

1.) The direction of the electric line of force is outward for positively charged particles, and inward for negatively charged particles.

Electric field line of positive charge

Electric field line of negative charge

So when two opposite charge are placed near each other, the electric line of force start from a positive charge and end at a negative charge

Electric lines of force of unlike charges

When two same nature charges are placed near each other, the field produced by one charge is equal and opposite to the field produced by the other charges at the midpoint of the line joining the two charges. Therefore, at this point, the resultant electric field is zero. This point is called the neutral point.

Electric lines of force of like charges

2.) The tangent drawn at any point on the line of force gives the direction of the force acting on a test-charged particle at that point.

3.) Two electric lines of force can never intersect with each other because if they do so then at the point of intersection two tangents can be drawn which would mean that there are two directions of the force at that point which is impossible.

4.) When electric lines of force are closer to each other, the electric field is stronger in this region. And where The line of force are far away from each other then the electric field is weaker in this region. When the line of force are parallel and in a straight line to each other, the electric field is known as the uniform electric field.

5.) The electric line of force has a tendency to contract in length like a stretched elastic string for the opposite nature of the charged particle. It is due to the attraction force between charged particles.

6.) The electric line of force has a tendency to separate from each other in the direction perpendicular to their length for the same nature of charged particles. It is due to the repulsion force between charged particles.

7.) The electric lines of force can never form closed loops as a line can never start and end on the same charge.

8.) The electric line of force also gives us an indication of the equipotential surface (That surface which has the same potential on each point of the surface).

9.) The electric line of force always flows from higher potential to lower potential.

10.) In a region where there is no electric field, lines are absent so the electric field inside the conductor is zero. Electric lines of force end or start normally from the surface of a conductor.

Read More

Electric Charge and its properties

What is an electric charge?

Electric charge is an intrinsic property of elementary particles (i.e. electron, proton and neutron etc.) of any substance which gives rise to electric force between them elementary particles.

Types of charge:

There are two types of electric charge

1. Positive Electric Charge like Proton
2. Negative Electric Charge like Electron

The same nature of charged particles repels each other and the opposite nature of charged particles attracts each other. For example, electrons and electrons repel each other, and electrons and protons attract each other. Similarly, proton and proton repel each other.

Generally, any substance is electrically neutral because the number of electrons and protons are equal in it but according to the Free electron Model theory, these substances are classified into three categories. These are:

1. Conductor
2. Semiconductor
3. Insulator

The electric force is generated in conductors and insulating substances but not in semiconductor substances because these semiconductor substances have four electrons in their valence shells.

Generation of Electric force in Conductor: The electric force is generated in conductors due to the transfer of electrons from one conducting substance to another conducting substance. There are various methods for the transfer of electrons in conductors, like contact, friction, and induction. Therefore, When electrons are transferred from one conductor to another conductor then the conductor has deficiency or excess of electrons, these conductors are called electrostatically charged.

Electrostatic charged Conductors:

 The charge on the conductors due to the transfer of electrons between the conductors is known as electrostatic charged conductor.

There are two types of electrostatic-charged conductors.

1.) Positive Electrostatic Charged Conductor:

When conductors have a deficiency of electrons i.e. the number of electrons is less than protons, these conductors are called positive electrostatic charged conductors.

2.) Negative Electrostatic Charged Conductor:

When conductors have excessive electrons i.e. number of electrons is greater than protons, these conductors are called negative electrostatic charged conductors.

Generation of Electric force in Insulator: Insulators are charged by induction this charging occurs due to the polarization of atoms of insulating substances. In the absence of an external electric field, the center of mass of the nucleus and electron cloud in an atom lies on the same point but when an insulating substance is placed in an external electric field, the center of mass of the nucleus and electron cloud in an atom is separated from each other at a very small distance. The center of mass of the electron cloud is shifted toward the positive side of the external electric field and the center of mass of the nucleus is shifted toward the negative side of the external electric field. thus these atoms are polarized. When insulators are electrically charged, these polarized atoms store the electric potential energy.

Basic Properties of Electric Charge:

1.) Additive Nature of Charge:

The total charge on any system is always equal to the algebraic sum of all the charges in the system.

If a system contains $'n'$ number of point charges, the total charge of a system will be the sum of $'n'$ number of point charges.

Let us consider, a system containing $'n'$ number of point charges like $q_{1},q_{2},q_{3}......q_{n}$, the total charge of the system will be

$Q=q_{1}+q_{2}+q_{3},.....+q_{n}$

$Q=\sum_{i}^{n}q_{i}$

2.) Conservation of Charge:

The total Charge of the isolated system is always conserved i.e.

“ Electric charge neither can be created nor destroyed i.e. The electric charge is only transfer from one subtance to another substance”.

3.) Quantization of Charge:

The electric charge is always an integer multiple of $‘e’$. It is known as the quantization of charge.

$Q=\pm ne$

Where $'n'$ is an integer number.

4.) The mass of charged particle depends on velocity:

The velocity of the charged particle is significant to the speed of light so the mass of the charged particle depends on the velocity. This variation can be found by following the formula:

$m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$

Where
$m_{0}$ - Rest mass of particle
$m$ - Relative mass of the particle

Read More

Electric Potential and Derivation of electric potential at a point due to point charged particle

Electric Potential:

When a test-charged particle is brought from infinity to a point in the electric field then the work done per unit test charge particle is called electric potential. It is represented by $V$. It is a scalar quantity.

Let's consider a test-charged particle $q_{0}$ bring from infinity to at a point $P$ in the electric field. If the work done by test charged particle is $W$ then electric potential →

$V=\frac{W}{q_{0}}$

Unit of Electric Potential: $Joul/Coulomb$  OR  $N-m/Ampere-sec$

In MKS: $Kg-m^{2}-Ampere^{-1}-sec^{-3}$

Dimension of Electric potential: $[ML^{2}A^{-1}T^{-3}]$

The electric potential at a point due to point charged particle:

Let us consider, a source point charge $+q$ is placed in air and vacuum at point $O$.Let's take a point $P$ at distance $r$ from the source point charged particle. Here the test-charged particle $+q_{0}$ is brought from infinity to point $P$.If the test-charged particle moves a very small distance $dx$ from point $A$ to $B$ against the electrostatic force. So electrostatic force at point $A$ which is placed at a distance $x$ from point $O$ →

$F=\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}} \qquad(1)$    

Electric potential due to point charge

The work is done against the electrostatic force $\overrightarrow{F}$ to move small distance $dx$ from point $A$ to Point $B$

$ dW=\overrightarrow{F}\: \overrightarrow{dx}$

$ dW=F\: dx \: cos 180^{\circ}$

Here the angle between the electrostatic force and displacement is $180^{\circ}$. So work done

$ dW=- F\: dx$

$ dW=-\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}}\:dx \qquad \left\{ from\: equation \: (1) \right\}$

The total work is done in moving the charge $q_{0}$ from infinity to the point $P$ will be

$W=-\int_{0}^{W}{dW}$

Here negative sign shows that the work done from infinity to at point $P$ is stored in the form of potential energy between the charges.

$ W=-\int_{\infty}^{r}{\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}}\:dx }$

$ W=-\frac{qq_{0}}{4\pi\epsilon{0}} \int_{\infty}^{r}{\frac{dx}{x^{2}} }$

$W=-\frac{qq_{0}}{4\pi\epsilon{0}} \left [\frac{-1}{x} \right ]_{\infty}^{r}$

$ W=-\frac{qq_{0}}{4\pi\epsilon{0}} \left [-\frac{1}{r}-\frac{-1}{\infty} \right ]$

$W=\frac{qq_{0}}{4\pi\epsilon{0}} \left [\frac{1}{r} \right ]$

$ W=\frac{1}{4\pi\epsilon{0}} \left [\frac{qq_{0}}{r} \right ]$

Hence, the work is done to move a unit test charge from infinity to the point $P$, or the electric potential at point $P$ is →

$V=\frac{W}{q_{0}}$

$V=\frac{1}{4\pi\epsilon{0}} \frac{q}{r}$

Read More

The electric potential energy of a system of Charges

The Potential Energy of a system of two-point like charges→

When the system of two charged particles is configured, in which one charge is at rest of position and another is brought from infinity to near the first charge then the work done acquire by this charged particle is stored in the form of electric potential energy between these charges.

Derivation→

Let us consider, If two charge $q_{1}$ and $q_{2}$ in which one charge $q_{1}$ is at the rest of the position at point $P_{1}$ and another charge $q_{2}$ is brought from infinity to a point $P$ to configure the system then the electric potential at point $P_{2}$ due to charge particle $q_{1}$ →

Electric potential energy between two like charges

$V=\frac{1}{4\pi\epsilon_{0}}\frac{q_{1}}{r}$

Where $r$ is the distance between the point $P_{1}$ and Point $P_{2}$

Here, Charge $q_{2}$ is moved in from infinity to point $P_{2}$ then the work required is →

$W=V q_{2}$

$W= \frac{1}{4\pi\epsilon_{0}}\frac{q_{1}q_{2}}{r}$

Since the electric potential at infinity is zero so work- done will also be zero. So total work done from infinity to a point $P$ will be stored in the form of electric potential energy.

$U=W$

$ U= \frac{1}{4\pi\epsilon_{0}}\frac{q_{1}q_{2}}{r}$

The electric potential energy of a system of three-point-like charges→

To obtain the potential energy of a system of three charges. First, obtain the work done between any two charges and then obtain the different work done for both those charges from the third charge and then the total work done will be equal to electric potential energy.

Let us consider a system is made up of three charges $q_{1}$, $q_{2}$ and $q_{3}$ which placed at point $P_{1}$,$P_{2}$ and $P_{3}$. Now the work done between two charges $q_{1}$ and $q_{2}$ is

Electric potential energy between three like charges

$W_{1}=\frac{1}{4\pi\epsilon_{0}}\frac{q_{1}q_{2}}{r_{12}}$

Now, the charge $q_{3}$ is brought from infinity to the point $P_{3}$. Work has to be done against the forces exerted by $q_{1}$ and $q_{2}$ Therefore, The work done between charges of $q_{2}$ and $q_{3}$

$W_{2}=\frac{1}{4\pi\epsilon_{0}} \frac{q_{2}q_{3}}{r_{23}}$

Now, The work done between charges $q_{1}$ and $q_{3}$

$ W_{3}=\frac{1}{4\pi\epsilon_{0}} \frac{q_{1}q_{3}}{r_{13}}$

The total work done to make a system of three charges:

$ W=W_{1}+W_{2}++W_{3}$

Now substitute the value of $W_{1}$, $W_{2}$and $W_{2}$ in above equation i.e.

$ W=\frac{1}{4\pi\epsilon_{0}} \left[\frac{q_{1}q_{2}}{r_{12}}+\frac{q_{1}q_{3}}{r_{13}}+\frac{q_{2}q_{3}}{r_{23}}\right]$

This work is stored in the form of electric potential energy in the system.

$U=W$

$ U=\frac{1}{4\pi\epsilon_{0}} \left[\frac{q_{1}q_{2}}{r_{12}}+ \frac{q_{1}q_{3}}{r_{13}}+\frac{q_{2}q_{3}}{r_{23}}\right]$

Similarly, the Potential energy of a system of N point system i.e.

$ U=\frac{1}{4\pi\epsilon_{0}} \sum_{i=1}^{N}\sum_{j=1}^{N}\frac{q_{i}q_{j}}{r_{ij}}$

Here $i\neq j$

Read More

Gauss's Law for Electric Flux and Derivation

Gauss's Law:

Gauss's law for electric flux is given by Carl Friedrich Gauss in 1813. He extended the work of Joseph-Louis Lagrange. This formula was first formulated in 1713 by Lagrange. Gauss's law stated that:

The electric flux passing normal through any closed hypothetical surface is always equal to the $\frac{1}{\epsilon_{0}}$ times of the total charge enclosed within that closed surface. This closed hypothetical surface is known as Gaussian surface.

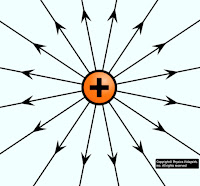
Let us consider that a $+q$ coulomb charge is enclosed within the Gaussian's surface. Then according to Gauss's Law, the electric flux will be:

$\phi _{E}= \frac{q}{\epsilon_{0}}$

The electric flux of the electric field →

$\phi_{E}=\oint \overrightarrow{E}\cdot\overrightarrow{dA}$

Substitute this value of electric flux $\phi_{E}$ in the above formula so we get →

$\oint \overrightarrow{E}\cdot\overrightarrow{dA}=\frac{q}{\epsilon_{0}}$

Where $\epsilon_{0}$ → Permittivity of the free space

The above formula of Gauss's law is applicable only under the following two conditions:

1. The electric field at every point on the surface is either perpendicular or tangential.


2. The magnitude of the electric field at every point where it is perpendicular to the surface has a constant value.

Derivation of Gauss's law from Coulomb's law:

1. When the charge is within the surface


2. When the charge is outside the surface

1. When the charge is within the surface:

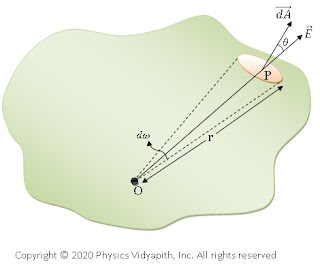
Let a charge $+q$ is placed at point $O$ within a closed surface of irregular shape. Consider a point $P$ on the surface which is at a distance $r$ from the point $O$. Now take a small element or area $\overrightarrow{dA}$ around the point $P$. If $\theta$ is the angle between $\overrightarrow{E}$ and $\overrightarrow{dA}$ then electric flux through small element or area $\overrightarrow{dA}$

$d\phi_{E}=\overrightarrow{E}\cdot\overrightarrow{dA}$

$d\phi_{E}=E\:dA\:cos\theta \qquad\quad\quad (1)$

When charge is inside the surface

According to Coulomb's law, the electric field intensity $E$  at point $P$.

$E=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r^{2}}$

Now substitute the value of electric field intensity $E$ in equation $(1)$

$d\phi_{E}=\frac{q}{4\pi\epsilon_{0}}\frac{dA\:cos\theta}{r^{2}}$

but $\frac{dA\:cos\theta}{r^{2}}$ is the solid angle $d\omega$ subtended by $dA$ at point $O$. Hence the above equation can be written as

$d\phi_{E}=\frac{q}{4\pi\epsilon_{0}}d\omega$

So, The total flux $\phi_{E}$ over the entire surface can be found by integrating the above equation

$\oint d\phi_{E}= \frac{q}{4\pi\epsilon_{0}}\oint d\omega$

For entire surface solid angle $d\omega$ will be equal to $4\pi$ i.e. $d\omega=4\pi$

$\phi _{E}= \frac{q}{\epsilon_{0}}$

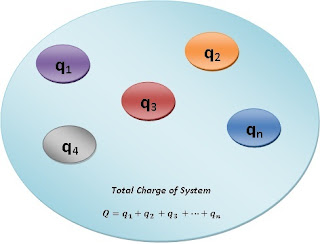
If the closed surface enclosed with several charges like $q_{1},q_{2},q_{3},.....-q_{1},-q_{2},-q_{3},.....$. Now each charge will contribute to the total electric flux $\phi_{E}$.

$\phi_{E}= \frac{1}{\epsilon_{0}}\left [ q_{1}+q_{2}+q_{3}...-q_{1}-q_{2}-q_{3}... \right ]$

Here $\quad q=q_{i}-q_{j}$

$\phi_{E}= \frac{1}{\epsilon_{0}}\sum_{i=1,j=1}^{n}(q_{i}-q_{j})$

$\phi_{E}= \frac{1}{\epsilon_{0}}\sum q$

Where $\sum q$ → Algebraic Sum of all the charges

2. When the charge is outside the surface:

Let a point charge $+q$ be situated at point $O$ outside the closed surface. Now a cone of solid angle $d\omega$ from point $O$ cuts the surface area $dA_{1}$, $dA_{2}$, $dA_{3}$, $dA_{4}$ at pont $P$, $Q$, $R$ and $S$ respectively. The electric flux for an outward normal is positive while for inward normal is negative so

The electric flux at point $P$ through area

$d\phi_{1}$= $-\left (\frac{q}{4\pi \epsilon_{0}} \right )d\omega$ The electric flux at point $Q$ through area

$d\phi_{2}$= $+\left (\frac{q}{4\pi \epsilon_{0}} \right )d\omega$

The electric flux at point $R$ through area

$d\phi_{3}$= $-\left (\frac{q}{4\pi \epsilon_{0}} \right )d\omega$

The electric flux at point $S$ through area

$d\phi_{4}$= $+\left (\frac{q}{4\pi \epsilon_{0}} \right )d\omega$

Charge is outside the surface

The Total electric flux will be sum of all the electric flux passing through areas of surface →

$\phi_{E}=d\phi_{1}+d\phi_{2}+d\phi_{3}+d\phi_{4}$

$\phi_{E}=-\left ( \frac{q}{4\pi \epsilon_{0}} \right )d\omega+\left ( \frac{q}{4\pi \epsilon_{0}} \right )d\omega \\ \qquad \: -\left ( \frac{q}{4\pi \epsilon_{0}} \right )d\omega+\left ( \frac{q}{4\pi \epsilon_{0}} \right )d\omega$

$\phi_{E}=0$

The above equation is true for all cones from point $O$ through any surface, however irregular it may be-

The total electric flux over the entire surface due to an external charge is zero.

This verifies Gauss's law.

Application of Gauss's law:

There are following some important application given below:

1. Electric field intensity due to a point charge


2. Electric field intensity due to uniformly charged spherical Shell (for Thin and Thick)


3. Electric field intensity due to a uniformly charged solid sphere (Conducting and Non-conducting)


4. Electric field intensity due to uniformly charged infinite plane sheet (for Thin and Thick)


5. Electric field intensity due to uniformly charged parallel sheet


6. Electric field intensity due to charged infinite length wire

Read More

Vector Form of Coulomb's Law

Derivation of vector form of Coulomb's law:

Let us consider, Two-point charges $+q_{1}$ and $+q_{2}$ are separated at a distance $r$ (magnitude only) in a vacuum as shown in the figure given below.

Let $\overrightarrow{F_{12}}$ is the force on charge $+q_{1}$ due to charge $+q_{2}$ and $\overrightarrow{F_{21}}$ is the force on charge $+q_{2}$ due to charge $+q_{1}$. Then

$\overrightarrow{F_{12}}=\frac{1}{4\pi \varepsilon _{0}}\frac{q_{1}q_{2}}{r^2}\:\:\hat{r_{21}}\qquad(1)$

Where $\widehat{r}_{21}$ ➝ Unit Vector Pointing from charge $+q_{2}$ to charge $+q_{1}$

$\overrightarrow{F_{21}}=\frac{1}{4\pi \varepsilon _{0}}\frac{q_{1}q_{2}}{r^2}\:\:\hat{r_{12}}\qquad(2)$

Where$\widehat{r}_{12}$ ➝ Unit Vector Pointing from charge $+q_{1}$ to charge $+q_{2}$

From the above figure, we can conclude that the direction of unit vector $\widehat{r}_{12}$ and $\widehat{r}_{21}$ is opposite. i.e.

$\hat{r_{12}}=-\hat{r_{21}}\qquad(3)$

So from equation $(2)$ and equation $(3)$, we can write as

$\overrightarrow{F_{21}}=-\frac{1}{4\pi \varepsilon _{0}}\frac{q_{1}q_{2}}{r^2}\:\:\hat{r_{21}}\qquad(4)$

Now, Put the value of equation $(1)$ in equation $(4)$. So equation $(4)$, we can write as

$\overrightarrow{F_{21}}=-\overrightarrow{F_{12}}\qquad (5)$

The above equation $(5)$ shows that " The Coulomb's force is Action and Reaction Pair. This force acts on different bodies." If

$\overrightarrow{F_{12}}=\overrightarrow{F_{21}}=\overrightarrow{F}$

And

$ \hat{r_{12}}=\hat{r_{21}}=\hat{r}$

Then generalized vector form of Coulomb's Law$\overrightarrow{F}=\frac{1}{4\pi\varepsilon _{0}}\frac{q_{1}q_{2}}{r^2}\:\hat{r}$

Where $\hat{r}=\frac{\overrightarrow{r}}{r}$

$ \overrightarrow{F}=\frac{1}{4\pi \varepsilon _{0}}\frac{q_{1}q_{2}}{r^3}\:\overrightarrow{r}$

Where $\overrightarrow{r}$ is displacement vector

This is a generalized vector form of Coulomb's law.

Read More

Coulomb′s Law and Applications

Coulomb’s Law: This law was first published by French physicist Charles-Augustin de Coulomb in the year 1785. According to Coulomb’s Law-

The electric force acting between the two point charges is directly proportional to the product of magnitude of the two charges and inversely proportional to square of the distance between these two charges. The electric force always acts along the line joining the charges.

Coulomb's force between the two charges

Let us consider two positive charges whose magnitude $q_{1}$ and $q_{2}$ are placed at a distance $‘r’$. According to Coulomb’s Law (magnitude only):

$F\propto q_{1}q_{2} \qquad(1)$

$F\propto \frac{1}{r^{2}} \qquad(2)$

From equation$(1)$ and equation$(2)$, we can write as:

$F\propto \frac{q_{1}q_{2}}{r^{2}} \qquad(3)$

$F=\frac{1}{4\pi \varepsilon K} \frac{q_{1}q_{2}}{r^{2}} \qquad(4)$

Where
$\epsilon$= Permittivity of any medium,
$K$ = Dielectric constant

For air and vacuum:
$\epsilon= \epsilon_{0}$ and $K=1$

So Coulomb’s Law for Air and Vacuum:

$F=\frac{1}{4\pi \varepsilon_{0}}\frac{q_{1}q_{2}}{r^{2}} \qquad(5)$

Where $\varepsilon _{0}=8.0854 \times 10^{-12} \:\: C^{2}N^{-1}m^{-2}$

Then, the value of $\frac{1}{4\pi \varepsilon_{0}}=9\times10^{9} N-m^{2}/C^{2}$ So, From Equation$(5)$

$F=9\times 10^{9} \frac{q_{1}q_{2}}{r^{2}}$

This is the equation of Coulomb's Law that applies to the medium of air or vacuum. The above equation of Coulomb Law shows only the magnitude value of electrostatic force.

Properties of Coulomb's law:-

There are the following properties of Coulomb's law:-

1. Coulomb force is an action and reaction pair and follows Newton's third law.


2. Coulomb force is a conservative force.


3. Coulomb force is central force i.e. it is always acting along the line joining between two charges.


4. If the net force is zero then momentum will be conserved.


5. If the center of mass is at rest and momentum is conserved then it follows the mass conservation law.


6. The force between two charges is independent of the presence or absence of other charges but the net force increases on that particular charge.

Limitation of Coulomb's Law:

1. This law does not apply to moving charges i.e. it applies to static charges (charge at rest) and charges must be stationary relative to each other.


2. It applies to charges of regular and smooth shape. It is very difficult to apply to irregular shapes.


3. The charges must not overlap for example they must be distinct point charges.


4. This law can not be directly applicable to calculate the charge on big planets.

Application of Coulomb's Law:

1. Coulomb's law is used to calculate the distance between the charges.


2. Coulomb's law is used to calculate the electrostatic force between the charges.


3. Coulomb's law is used to calculate the electrostatic force on a point charge due to the presence of several point charges. It is also known as the Superposition theorem of electrostatic force.

**What is $1$ Coulomb's?

Answer: When two unit charges are placed in a vacuum at one meter apart then the force acting between charges is $9\times10^{9}$ $N$.This force is known as 1 Coulomb.

Read More