Interference of light:
When two or more waves, having the same frequency and constant phase difference, travel simultaneously in the same region of a medium, these waves superimpose on each other and a resultant wave is obtained which has intensity at some points maximum and some points minimum in the region. This is phenomenon is known as interference of light.
When the intensity of the resultant wave is maximum in the region then this is called constructive interference.
when the intensity of the resultant wave is minimum in the region then this is called destructive interference.
Classification of Interference:
The phenomenon of interference may be grouped into two categories depending upon the formation of two coherent sources in practice.The interference of light is classified into two categories:
Division of amplitude
Division of wavefront
Division of amplitude:
In this method, the amplitude of the incident beam is divided into two or more parts are either by partial reflection or refraction. the beams travel in different paths, are superimposed on each other, and form the interference pattern.
Example:
Interference in the thin film, Newton's rings, and Michelson's interferometer are examples of two-beam interference and Fabry-Perot interferometer is the example of multiple-beam interference.
Division of Wavefront:
Under this category, the coherent sources are obtained by dividing the wavefront, originating from a common source, by employing mirrors, biprisms, or lenses. This class of interference requires initially a point source or a narrow slit source. The instruments used to obtain coherent sources and hence interference by division of wavefront are fresnel biprism fresnel Mila mirror Lloyd's mirror laser etc.
Showing posts with label Optics. Show all posts
Showing posts with label Optics. Show all posts
 February 09, 2022
February 09, 2022 Physics Vidyapith
Physics Vidyapith Optics
Optics
Newton's Rings:
Experimental Arrangement:
A plano-convex lens $l_{1}$ of large radius of curvature is placed on a plane glass plate $G_{1}$ with the curved surface touching the glass plate.
An air film is enclosed between the curved surface of the lens and the glass plate.
A sodium vapor lamp $S$ is kept at the focus of a biconvex lens $L$ which converts the diverging beam of light into a parallel beam. The parallel beam of light is made to fall on a glass plate $G_{2}$ kept at an angle of $45^{\circ}$ with the incident beam.
A part of incident light is reflected toward the plano-convex lens. This light is again reflected back, partially from the top and partially from the bottom of the air fil and transmitted by the glass plate $G_{2}$. The interference of these rays is observed through a microscope $M$.
Explanation of the formation of Newton's rings:
Division of amplitude takes place at the curved surface of the plano-convex lens.
The incident light is partially reflected and partially transmitted at the curved surface.
The transmitted ray is reflected from the glass plate. These two rays interfere in reflected light
The path difference between these rays depends on the thickness of the air film enclosed between the curved surfaces of the lens and glass plate which increases radially outward from the center. The thickness of the air film is zero at the center
Path difference:
Let $t$ is the thickness of air film at a radial distance of $r$ and $R$ is the radius of curvature. So the path difference for a wedge-shaped film is
$\Delta=2 \mu t \: cos(r+\alpha) \pm \frac{\lambda}{2} \qquad(1)$
HereRefractive index of air film ($\mu)=1$$\alpha$ is very small i.e. $\alpha \approx 0$For normal incidence $r=0$ i.e $cos(\alpha+r)=1$
Now apply the above condition to equation $(1)$ then we get
$\Delta = 2t + \frac{\lambda}{2} \qquad(2)$
Form figure, In $\Delta OAB$, apply the Pythagoras theorem
$OA^{2}=OB^{2}+AB^{2}$
$R^{2}=(R-t)^{2}+r^{2}$
$R^{2}=R^{2}+t^{2}-2Rt+r^{2}$
$2Rt=t^{2}+r^{2}$
As $t$ is very small, $t^{2}$ can be neglected in comparison with $r^{2}$. So
$2Rt=r^{2}$
$2t=\frac{r^{2}}{R} \qquad(3)$
Here $r$- Radius of a circle for which thickness is $t$
If $D$ is the diameter of this circle then
$r=\frac{D}{2}$
So from equation $(3)$
$2t=\frac{D^{2}}{4R} \qquad(4)$
Substitute the value of $2t$ in equation $(2)$ then we get
$\Delta = \frac{D^{2}}{4R}+\frac{\lambda}{2}$
Diameter of Bright rings:
For bright rings, the condition for constructive interference is satisfied. i.e.
$\Delta =n \lambda$
So from the above equations, we get
$\frac{D^{2}}{4R}+\frac{\lambda}{2}=n \lambda $
Where $D_{n}$- Diameter of the $n^{th}$ bright ring
$\frac{D^{2}}{4R}=(2n-1) \frac{\lambda}{2}$
$D_{n}= \sqrt {2 \lambda R (2n-1)}$
Where $n=1,2,3,4........$
$D_{n} \propto \sqrt{(2n-1)}$
i.e The diameter of the bright rings are proportional to the square root of odd natural numbers.
Diameter of Dark ring:
Condition for destructive interference is satisfied for dark rings i.e.
$\Delta=(2n+1)\frac{\lambda}{2}$
$\frac{D^{2}}{4R}+\frac{\lambda}{2}=(2n+1)\frac{\lambda}{2}$
$\frac{D^{2}}{4R}+\frac{\lambda}{2}=n \lambda + \frac{\lambda}{2}$
$\frac{D^{2}}{4R}=n \lambda$
$D_{n}= \sqrt{4Rn\lambda}$
$D_{n} \propto \sqrt{n}$
Where $n=1,2,3,4........$
i.e The diameter of dark rings are proportional to square root of natural numbers.
 |
| Newtons Rings Experiment Setup-Ray Diagram |
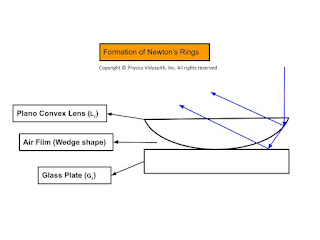 |
| Formation of Newton Rings |
 |
| Newton’s Rings Diagram for Path difference Formula Calculation |
 February 08, 2022
February 08, 2022 Physics Vidyapith
Physics Vidyapith Optics
Optics
Derivation of Fringe width of the wedge-shaped thin film:
The distance between two consecutive bright (or dark) fringes is called the fringe width.
If the $n^{th}$ bright fringe is formed at a distance $x_{n}$ from the edge of the wedge shaped film where the thickness is $t_{n}$. So the path difference for $x_{n}$ bright fringe:
$(2n-1) \frac{\lambda}{2}= 2 \mu \: t_{n} \: cos(\alpha+r) \qquad(1)$
For Normal IncidenceThe incident Angle $i=0$The refracted Angle $r=0$
then from equation $(1)$
$(2n-1) \frac{\lambda}{2}= 2 \mu \: t_{n} \: cos\alpha \qquad(2)$
From the figure, In $\Delta OAB$
$tan \alpha = \frac{t_{n}}{x_{n}}$
$t_{n}=x_{n} \: tan \alpha \qquad(3) $
Now put the value of $t_{n}$ in equation $(2)$
$(2n-1) \frac{\lambda}{2}= 2 \mu \: x_{n} \: tan \alpha \: cos\alpha $
$(2n-1) \frac{\lambda}{2}= 2 \mu \: x_{n}\: \frac{sin \alpha}{cos\alpha} \: cos\alpha $
$(2n-1) \frac{\lambda}{2}= 2 \mu \: x_{n} \: sin \alpha \qquad(4)$
Similarly for $(n+1)^{th}$ bright fringe i.e put the $(n+1)$ in place of $n$ in above equation then we get
$\left\{ 2(n+1)-1 \right\} \frac{\lambda}{2}= 2 \mu \: x_{n+1} \: sin \alpha $
$(2n+1) \frac{\lambda}{2}= 2 \mu \: x_{n+1} \: sin \alpha \qquad(5)$
Subtract the equation $(5)$ and equation$(4)$
$2\mu \: (x_{n+1}-x_{n})\: sin \alpha =\lambda$
$2\mu \beta \: sin \alpha =\lambda$
Where $\beta=$ fringe Width$(x_{n+1}-x_{n})$
$\beta=\frac{\lambda}{2\mu\: sin \alpha}$
If $\alpha$ is very small so $sin \alpha \approx \alpha$
$\beta=\frac{\lambda}{2\mu\: \alpha}$
 |
| Fringe width of wedge-shaped thin film for normal incidence |
 February 04, 2022
February 04, 2022 Physics Vidyapith
Physics Vidyapith Optics
Optics
Derivation of interference of light due to a wedge-shaped thin film:
The wedge-shaped film is bound by two plane surfaces inclined at angle $\alpha$.
The thickness t of the film varies uniformly from zero at the edge to its maximum value at the other end.
A Ray of light ab incident on the film will be partially reflected along be and partially transmitted along $BC$. The ray $BC$ will be partially reflected along $CD$ which will be again partially transmitted along $BF$. The two rays $BE$ and $DF$ in reflected light diverge.
The path difference between ray $BE$ and $DF$ is
$\Delta=\mu(BC+CD)-BG \qquad(1)$
Where $\mu$- Refractive index of the film
$\Delta CDJ$ and $\Delta CHJ$ are congruent so
$
\begin{Bmatrix}
CD=CH \\
DJ=JH=t
\end{Bmatrix}
\qquad(2)$
From equation $(1)$
$\Delta=\mu(BK+KC+CH)-BG \qquad (\because BD=BK+KC)$
$\Delta=\mu(BK+KH)-BG \qquad (3)$
In $\Delta BDG$-
$sin\:i = \frac{BG}{BD}$
$BG=BD sin \: i \qquad(4)$
In $\Delta BDK$
sin\:r =\frac{BK}{BD}
$BD=\frac{BK}{sin \: r} \qquad(5)$
From equation $(4)$ and equation $(5)$-
$BG=BK. \frac{sin \: i}{sin \: r}$
$BG=\mu . BK \qquad(6) \qquad (\because \mu=\frac{sin \: i}{sin \: r})$
Now put the value of $BG$ in equation $(3)$
$\Delta= \mu(BK+KH)- \mu. BK$
$\Delta= \mu.KH \qquad(7)$
In $\Delta DKH$
$cos \: (\alpha + r)= \frac{KH}{DH}$
$KH=DH \: cos \: (\alpha + r)$
$KH=(DJ+JH) \: cos \: (\alpha + r)$
$KH=2t \: cos \: (\alpha + r) \qquad(8) $ {From equation $(2)$}
Now put the value of $KH$ in equation $(7)$
$\Delta= 2\mu t \: cos \: (\alpha + r)$
The ray $DF$ suffers a phase change of $\pi$ due to reflection from a denser medium at $C$. Whereas there is not any change in phase due to reflection for ray $BE$.
$\Delta= 2\mu t \: cos \: (\alpha + r) \pm \frac{\lambda}{2}$
For Constructive Interference:
$\Delta= n \lambda$
$\Delta= 2\mu t \: cos \: (\alpha + r) \pm \frac{\lambda}{2}= n \lambda$
$ 2\mu t \: cos \: (\alpha + r)= (2n \pm 1) \frac{\lambda}{2}$
For Destructive Interference:
$\Delta= (2n \pm 1) \frac{\lambda}{2}$
$\Delta= 2\mu t \: cos \: (\alpha + r) \pm \frac{\lambda}{2}=(2n \pm 1) \frac{\lambda}{2}$
$\Delta= 2\mu t \: cos \: (\alpha + r) =2n \lambda$
 |
| Interference of light due to wedge-shaped thin film |
 February 02, 2022
February 02, 2022 Physics Vidyapith
Physics Vidyapith Optics
Optics
Derivation of interference of light due to thin-film:
Let's consider a Ray of light $AB$ incident on a thin film of thickness $t$ and the refractive index of a thin film is $\mu$
The ray $AB$ is partially reflected and partially transmitted at $B$. The transmitted BC is against partially transmitted and partially reflected at $C$. The reflected ray $CD$ is partially reflected and partially refracted at $D$.
The interference pattern in reflected light will be due to ray $BF$ and $DH$ which are coherent as they are both derived from the same Ray $AB$.
The interference pattern in transmitted light will be due to ray $CI$ and $EJ$.
The path difference between $BF$ and $DH$ ray will be
$\Delta=\mu(BC+CD)-BG \qquad(1)$
The triangle $\Delta BCK$ and $\Delta CDK$ are congruent because
$\begin{Bmatrix}
BK=KD
\\
BC=CD
\\
CK=t \end{Bmatrix} \qquad (2)$
From equation $(1)$ and $(2)$
$\Delta=2 \mu BC-BG \qquad(3)$
In $\Delta BCK$
$cos \: r= \frac{CK}{BC}$
$BC= \frac{t}{cos \: r} \qquad(4)$
In $\Delta BGD$
$sin \: i= \frac{BG}{BD}$
$BG= BD \: sin\: i $
$BG= (BK+KD)\: sin\: i $
$BG= 2BK \: sin\: i \qquad(5)$ {From eqaution $(2)$}
Again In $\Delta BCK$
$tan \:r = \frac{BK}{CK}$
$BK=t.tan\:r \qquad(6)$
Put the value of $BK$ in equation $(5)$
$BG=2t\:sin \:i .tan\: r$
$BG=2t\:sin \:i .\frac{sin \: r}{cos \: r}$
$BG= 2t \frac{sin \:i}{sin \: r} \frac{sin^{2} \:r}{cos \: r}$
$BG=2\mu t \frac{sin^{2} \:r}{cos \: r} \qquad (7)\qquad \left( \mu =\frac{sin \:i}{sin \: r}\right)$
Now put the value of $BG$ and $BC$ in equation $(3)$
$\Delta= \frac{2 \mu t}{cos \: r}-2\mu t\frac{sin^{2} \:r}{cos \: r}$
$\Delta=\frac{2 \mu t}{cos \:r} \left[1-sin^{2} \:r \right]$
$\Delta=2 \mu t \frac{cos^{2} \:r}{cos \:r} $
$\Delta=2 \mu t \: cos \:r$
Interference in a reflected ray:
The ray $BF$ suffers phase change of $\pi$ due to reflection from the denser medium at $B$. Therefore the path difference of $\frac{\lambda}{2}$ is introduced between two rays due to reflection-
$\Delta= 2\mu t \: cos\:r \pm \frac{\lambda}{2}$
Constructive Interference due reflected ray:
for constructive interference
$\Delta=n \lambda$
so from the above equations, we get
$2\mu t \: cos\: r \pm \frac{\lambda}{2}=n \lambda$
$2\mu t \: cos\: r = (2n \pm 1)\frac{\lambda}{2}$
Destructive Interference due to reflected ray:
for destructive interference
$\Delta=(2n \pm 1)\frac{\lambda}{2}$
so from the above equations, we get
$2\mu t \: cos\: r \pm \frac{\lambda}{2}=(2n \pm 1)\frac{\lambda}{2}$
$2\mu t \: cos\: r =n \lambda$
Interference in transmitted ray:
The ray $CI$ and $EJ$ in transmitted Ray have the same path difference as a reflected ray. There is not any change in phase for $CI$ due to reflection as it gets transmitted at $C$. The ray $EJ$ also does not undergo phase change due to reflection as it is reflected from the rarer medium at $C$ and $D$.
$\Delta= 2\mu t \: cos\:r $
Constructive Interference due to transmitted ray:
for constructive interference
$\Delta=n \lambda$
so from the above equations, we get
$2\mu t \: cos\: r =n \lambda$
Destructive Interference due to transmitted ray:
for destructive interference
$\Delta=(2n \pm 1)\frac{\lambda}{2}$
so from the above equations, we get
$2\mu t \: cos\: r =(2n \pm 1)\frac{\lambda}{2}$
$2\mu t \: cos\: r =n \lambda$
 |
| Propagation of light ray in thin film |










