The area of parallel-plate = $A$
The distance between the parallel-plate = $d$
The dielectric constant of the slab of a material =$K$
The thickness of the material =$t$
The vacuum (or air) between the plates =$(d-t)$ The surface charge density on the plates= $\sigma$
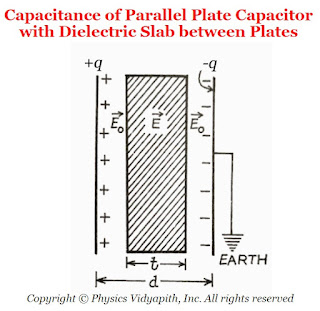 |
| The capacitance of Parallel Plate Capacitor with Dielectric Slab between Plates |
- When the dielectric slab is completely filled between the parallel plates i.e. $t=d$ then the capacitance between the parallel plates
$C= \frac{K \: \epsilon_{\circ}\: A}{d}$
- When there is a vacuum (or air) between the parallel plates i.e. $t=0$, then the capacitance between the parallel plates
$C_{\circ}= \frac{ \epsilon_{\circ}\: A}{d}$
- When there is a slab of metal whose dielectric constant is infinity (K=∞). If the thickness of the slab is t between the parallel plates, then the capacitance between the parallel plates
$C= \frac{ \: \epsilon_{\circ}\: A}{d-t}$
- When the slabs of dielectric constants $K_{1},K_{2},K_{3},K_{4}...........$ and respective thickness $t_{1},t_{2},t_{3},t_{4},........$ is placed in the entire space between the parallel-plates, then the capacitance between the plates
$C=\frac{\epsilon_{\circ} A}{d- \left( t_{1}+t_{2}+t_{3}+.... \right)+ \left( \frac{t_{1}}{K_{1}}+\frac{t_{2}}{K_{2}}+\frac{t_{3}}{K_{3}}+....... \right)}$But $d=t_{1}+t_{2}+t_{3}+....$$C=\frac{\epsilon_{\circ} A}{ \left( \frac{t_{1}}{K_{1}}+\frac{t_{2}}{K_{2}}+\frac{t_{3}}{K_{3}}+..... \right)}$




