Electric field intensity due to uniformly charged solid sphere (Conducting and Non-conducting)

A.) Electric field intensity at different points in the field due to the uniformly charged solid conducting sphere:

Let us consider, A solid conducting sphere that has a radius $R$ and charge $+q$ is distributed on the surface of the sphere in a uniform manner. Now find the electric field intensity at different points due to the solid-charged conducting sphere. These different points are:

1. Electric field intensity outside the solid conducting sphere
2. Electric field intensity on the surface of the solid conducting sphere
3. Electric field intensity inside the solid conducting sphere

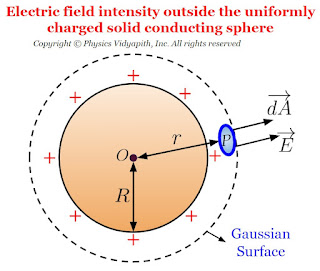
1.) Electric field intensity outside the solid conducting sphere:

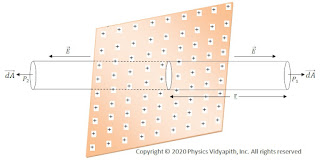
If $O$ is the center of solid conducting spherical then the electric field intensity outside of the sphere can be determined by the following steps →

1. First, take the point $P$ outside the sphere
2. Draw a spherical surface of radius r which passes through point $P$. This hypothetical surface is known as the Gaussian surface.
3. Now take a small area $\overrightarrow {dA} $ around point $P$ on the Gaussian surface to find the electric flux passing through it.
4. Now find the direction between the electric field vector and a small area vector.

Due to uniform charge distribution, the electric field intensity will be the same at every point on the Gaussian surface. So from the figure,

The direction of electric field intensity on the Gaussian surface is radially outward which is in the direction of the area vector of the Gaussian surface. i.e. ($\theta=0^{\circ}$). Here $\overrightarrow {dA}$ is a small area around point $P$ so the small electric flux $d\phi_{E}$ will pass through this small area $\overrightarrow {dA}$. so this flux can be found by applying Gauss's law in question given below:

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \quad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$ →

$ \oint d\phi_{E}= \oint E\:dA $

$\phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation $(2)$ and equation $(3)$, we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

Now substitute the area of the entire Gaussian spherical is $\oint {dA}=4\pi r^{2}$ in the above equation. So the above equation can be written as:

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged solid conducting sphere is the same as the entire charge is placed at the center, point charge

If the surface charge density is $\sigma$, Then the total charge $q$ on the surface of a solid conducting sphere is→

$ q=4\pi R^{2}\: \sigma$

Substitute this value of charge $q$ in the above equation, so we can write the equation as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi R^{2}\: \sigma}{r^{2}}$

$ E=\frac{\sigma}{\epsilon_{0}}\frac{R^{2}}{r^{2}}$

This equation describes the electric field intensity at the external point of the solid conducting sphere.

2.) Electric field intensity on the surface of the solid conducting sphere:

If point $P$ is placed on the surface of the solid conducting sphere i.e. ($r=R$). so electric field intensity on the surface of the solid conducting sphere can be found by putting $r=R$ in the formula of electric field intensity at the external point of the solid conducting sphere:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{R^{2}}$

$ E=\frac{\sigma}{\epsilon_{0}}$

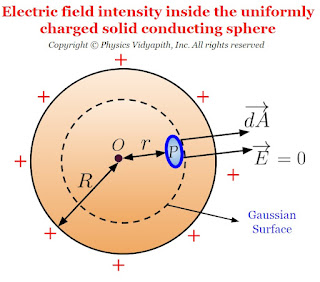
3.) Electric field intensity inside the solid conducting sphere:

If point $P$ is placed inside the solid conducting sphere then electric field intensity will be zero because the charge is distributed uniformly on the surface of the solid sphere and there will not be any charge on the Gaussian surface. So the electric flux will be zero inside the solid sphere. i.e.

$ \phi_{E}=\oint E\:dA$

$ 0=E\oint dA \qquad\quad \left \{ \because \phi_{E}=0 \right \}$

$ E=0$

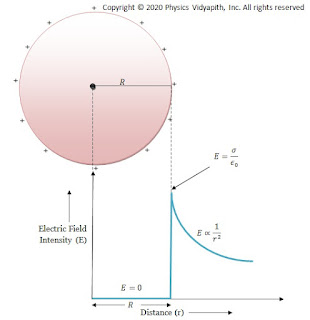
Electric field intensity distribution with distance for Conducting Solid Sphere:

Electric field intensity distribution with distance shows that the electric field is maximum on the surface of the sphere and zero inside the sphere. Electric field intensity distribution outside the sphere reduces with the distance according to $E=\frac{1}{r^{2}}$.

B.) Electric field intensity at different points in the field due to the uniformly charged solid non-conducting sphere:

Let us consider, A solid non-conducting sphere of radius R in which $+q$ charge is distributed uniformly in the entire volume of the sphere. So electric field intensity at a different point due to the solid charged non-conducting sphere:

1. Electric field intensity outside the solid non-conducting sphere
2. Electric field intensity on the surface of the solid non-conducting sphere
3. Electric field intensity inside the non-solid conducting sphere

1.) Electric field intensity outside the solid non-conducting sphere:

Let us consider, An external point $P$ which is at a distance $r$ from the center point $O$ of the sphere. The electric flux is radially outward in the sphere. So the direction of the electric field vector and the small area vector will be in the same direction i.e. ($\theta =0^{\circ}$). Here $\overrightarrow {dA}$ is a small area, the small amount of electric flux will pass through this area i.e. →

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \qquad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$ →

$ \phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation (1) and equation (2), we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

Now substitute the area of the entire Gaussian spherical surface is $\oint {dA}=4\pi r^{2}$ in the above equation. So the above equation can be written as:

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged solid non-conducting sphere is the same as the point charge i.e. like the entire charge is placed at the center.

Since the sphere is a non-conductor so the charge is distributed in the entire volume of the sphere. So charge distribution can calculate by volume charge density →

$q=\frac{4}{3} \pi R^{3} \rho $

Substitute this value of charge $q$ in the above equation, so we can write the equation as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi R^{3}\: \rho}{3r^{2}}$

$ E=\frac{\rho}{\epsilon_{0}}\frac{R^{3}}{3r^{2}}$

This equation describes the electric field intensity at the external point of the solid non-conducting sphere.

2.) Electric field intensity on the surface of the solid non-conducting sphere:

If point $P$ is placed on the surface of a solid non-conducting sphere i.e. ($r=R$). so electric field intensity on the surface of a solid non-conducting sphere can be found by putting $r=R$ in the formula of electric field intensity at the external point of the solid non-conducting sphere:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{R^{2}}$

$ E=\frac{\rho R}{3\epsilon_{0}}$

3.) Electric field intensity inside the solid non-conducting sphere:

If point $P$ is placed inside the sphere and the distance from the origin $O$ is $r$, the electric flux which is passing through the Gaussian surface

$ \phi_{E}= E.4\pi r^{2}$

Where $\phi_{E}=\frac{q'}{\epsilon_{0}}$

$ \frac{q'}{\epsilon_{0}}=E.4\pi r^{2}$

Where $q'$ is part of charge $q$ which is enclosed with Gaussian Surface

$ E=\frac{1}{4 \pi \epsilon_{0}} \frac{q'}{r^{2}} \qquad \qquad (4)$

The charge is distributed uniformly in the entire volume of the sphere so volume charge density $\rho$ will be the same as the entire solid sphere i.e.

$ \rho=\frac{q}{\frac{4}{3}\pi R^{3}}=\frac{q'}{\frac{4}{3}\pi r^{3}}$

$ \frac{q}{\frac{4}{3}\pi R^{3}}=\frac{q'}{\frac{4}{3}\pi r^{3}}$

$ q'=q\frac{r^{3}}{R^{3}}$

$ q'=q\left (\frac{r}{R} \right)^{3}$

Put the value of $q'$ in equation $(4)$, so

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}\left(\frac{r}{R} \right)^{3}$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{qr}{R^{3}}$

Where $q=\frac{4}{3} \pi R^{3} \rho $. So above equation can be written as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi R^{3} \rho r}{R^{3}}$

$E=\frac{ \rho r}{3 \epsilon_{0}}$

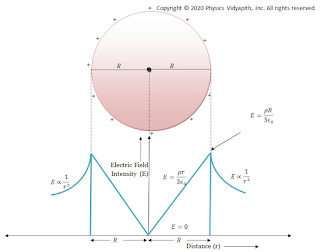
Electric field intensity distribution with distance for non-conducting Solid Sphere:

Electric field intensity distribution with distance shows that the electric field is maximum on the surface of the sphere and zero at the center of the sphere. Electric field intensity distribution outside the sphere reduces with the distance according to $E=\frac{1}{r^{2}}$.

Read More

Derivation of Planck's Radiation Law

Derivation: Let $ N$ be the total number of Planck’s oscillators and $E$ be their total energy, then the average energy per Planck’s oscillator is

$ \overline{E}=\frac{E_{N}}{N} \qquad (1)$

Let there be $ N_{0}, N_{1} ,N_{2} ,N_{3},---N_{n}$ oscillator having energy $ E_{0}, E_{1}, E_{2}, -- E_{n}$ respectively.

According to Maxwell’s distribution, the number of oscillators in the $ n^{th}$ energy state is related to the number of oscillators in the ground state by

$ N_{n}=N _{0} e^{\tfrac{-nh\nu }{kt} }\qquad (2)$

Where $ n$ is a positive integer. So put $ n= 1,2,3,…….$. The above equation can be written for different energy states. i.e.

$ N_{1}= N _{0} e^{\tfrac{-h\nu }{kt} }$

$ N_{2}= N _{0} e^{\tfrac{-2h\nu }{kt} }$

$ N_{3}= N _{0} e^{\tfrac{-3h\nu }{kt} }$

$.............$

$.............$

So, the total number of Planck’s Oscillators –

$ N= N _{0} +N_{1}+N_{2}+N_{3}+.... N_{n}$

$ N= N _{0} + N_{0} e^{\tfrac{-h\nu }{kt}}+ N_{0} e^{\tfrac{-2h\nu }{kt}}+...+ N_{0}e^{\tfrac{-nh\nu }{kt}}$

$ N= N _{0}[1+e^{\tfrac{-h\nu }{kt}}+e^{\tfrac{-2h\nu }{kt}}+.... e^{\tfrac{-nh\nu }{kt}}] \qquad(3)$

Let $ x = e^{\frac{-h\nu }{kt}} \qquad (4) $

Then $ N = N_{0}[1+x+x^{2}+x^{3}+...+ x^{n}]$

$ N = \frac{N_{0}}{1-x} \qquad(5)$ [ from Binomial theorem]

Now the total energy of oscillators –

$ E_{N} = E_{0}N_{0}+ E_{1}N_{1}+ E_{2}N_{2}+...+ E_{n}N_{n}$

$ E_{N } = 0.N_{0}+ h\nu N_{0} e^{\tfrac{-h\nu }{kt}}+...+nh\nu N_{0} e^{\tfrac{-nh\nu }{kt}}$

$ E_{N } = N_{0}h\nu (e^{\tfrac{-h\nu }{kt}}+2e^{\tfrac{-2h\nu }{kt}}+...+ ne^{\tfrac{-nh\nu }{kt}})$

From equation $(4)$ put $ x = e^{\tfrac{-h\nu }{kt}}$ in above equation. i.e

$ E_{N } = N_{0}h\nu (x+2x^{2}+3x^{3}+...+nx^{n}) $

$ E_{N } = N_{0}h\nu x(1+2x+3x^{2}+....)$

$ E_{N } = \frac{N_{0}h\nu x}{(1-x)^{2}} \qquad(6)$ (from Bionomical theorem)

Now substituting the value of $N$ from equation $ (5)$ and $ E_{n}$ from equation $ (6)$  in equation $ (1)$ –

$ \overline{E}= \frac{\frac{N_{0}h\nu x}{(1-x)^{2}}}{\frac{N_{0}}{(1-x)}}$

$ \overline{E}= \frac{h\nu }{(\frac{1}{x}-1)}$

$ \overline{E}= \frac{h\nu }{e^{\tfrac{h\nu }{kt}}-1} \qquad(7)$

The number of oscillators per unit volume in wavelength range to $ ( \lambda + d\lambda )$ is $\frac{8\pi }{\lambda ^{4}} d\lambda$.

The energy per unit volume $ (E_{\lambda }d\lambda )$ in the wavelength range to $( \lambda +d\lambda ) $ is –

$ E_{\lambda}d\lambda = \frac{8\pi }{\lambda ^{4}}d\lambda \overline{E} \qquad(8)$

From equation $ (7)$ and $ (8)$ –

$ E_{\lambda}d\lambda = \frac{8\pi }{\lambda ^{4}}d\lambda \frac{h\nu }{(e^{\tfrac{h\nu}{kt}}-1)}$

$ E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}} \frac{d\lambda}{(e^{\tfrac{hc}{\lambda kt}}-1)}$

The above equation describes Planck’s radiation law and this law was able to thoroughly explain the black body radiation spectrum.

Wien’s Displacement law from Planck’s Radiation Law:

Planck’s radiation law gives the energy in wavelength region $ \lambda to \lambda +d\lambda $ as –

$ E_{\lambda}d \lambda = \frac{8\pi hc}{\lambda ^{5}}(\frac{1}{e^{\tfrac{hc}{\lambda kt}}-1})d\lambda \qquad(1)$

For shorter wavelength $ \lambda T$ will be small and hence

$ e^{\tfrac{hc}{\lambda kt}}> > 1$

Hence, for a small value of $\lambda T$ Planck’s formula reduces to -

$ E_{\lambda}d \lambda = \frac{8\pi hc}{\lambda ^{5}}(\frac{1}{e^{\tfrac{hc}{\lambda kt}}}) d\lambda$

$ E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}}e^{\tfrac{-hc}{\lambda kt}}d\lambda$

$E_{\lambda}d\lambda = A \lambda ^{-5} e^{\tfrac{-hc}{\lambda kt}}d\lambda$

Where $ A = 8\pi hc$

The above equation is Wien’s law of energy distribution verified by Planck radiation law.

Rayleigh-Jeans law from Planck’s Radiation Law:

According to Planck’s radiation law –

$ E_{\lambda}.d\lambda = \frac{8\pi hc}{\lambda ^{5}}\frac{1 }{e^{\tfrac{hc}{\lambda kt}}-1}.d\lambda$

For longer wavelength $ e^{\frac{hc}{\lambda kt}}$ is small and can be expanded as-

$ e^{\tfrac{hc}{\lambda kt}} = 1+\frac{hc}{\lambda kt}+\frac{1}{2!}(\frac{hc}{\lambda kt})^{2}+....$

Neglecting the higher-order term –

$ e^{\tfrac{hc}{\lambda kt}} = 1+\frac{hc}{\lambda kt}$

Hence for longer wavelength, Planck’s formula reduces to –

$ E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{5}}[\frac{1}{1+\frac{hc}{\lambda kt}-1}]$

$ E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{4}}.d\lambda$

This is Rayleigh Jean’s law verified by Planck Radiation Law.

Read More

Orthogonality of the wave functions of a particle in one dimension box or infinite potential well

Description of Orthogonality of the wave functions of a particle in one dimension box or infinite potential well:

Let $\psi_{n}(x)$ and $\psi_{m}(x)$ be the normalized wave functions of a particle in the interval $(0, L)$ corresponding to the different energy level $E_{n}$ and $E_{m}$ respectively. These wave functions are:

$\psi_{n}(x)= \sqrt{\frac{2}{L}} sin \frac{n \pi x}{L}$

$\psi_{m}(x)= \sqrt{\frac{2}{L}} sin \frac{m \pi x}{L}$

Where $m$ and $n$ are integers.

In this function are real. Therefore

$\psi_{n}^{*}(x) = \psi_{n}(x)$

$\psi_{m}^{*}(x) = \psi_{m}(x)$

Where $m=n$,

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx = \frac{2}{L} \int_{0}^{L} sin \frac{m \pi x}{L} . sin \frac{n \pi x}{L} dx$

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \int_{0}^{L} \left[ cos \left\{ \frac{(m-n) \pi x}{L} \right\} - cos \left\{ \frac{(m+n) \pi x}{L} \right\} \right] dx $

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \left[ \frac{L}{\pi(m-n)} sin \left\{ \frac{(m-n) \pi x}{L} \right\} - \frac{L}{\pi(m+n)} sin \left\{ \frac{(m+n) \pi x}{L} \right\} \right]_{0}^{L} $

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \left[ \frac{L}{\pi(m-n)} sin \left\{ \frac{(m-n) \pi x}{L} \right\} - \frac{L}{\pi(m+n)} sin \left\{ \frac{(m+n) \pi x}{L} \right\} \right]_{0}^{L} $

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =0$

Hence, The function is mutually orthogonal in the interval $(0, L)$. These functions $\psi_{n}(x)$ and $\psi_{m}(x)$ are also normalized in this interval. The wave function, which is normalized and mutually orthogonal in an interval is said to form an orthogonal set in this interval. Since the wave function are zero outside the interval $(0, L)$, they are also orthogonal wave function in the whole range of $x$ axis in the interval $(-\infty, +\infty)$.

Read More

The electric potential at different points (like on the axis, equatorial, and at any other point) of the electric dipole

Electric Potential due to an Electric Dipole:

The electric potential due to an electric dipole can be measured at different points:

1. The electric potential on the axis of the electric dipole


2. The electric potential on the equatorial line of the electric dipole


3. The electric potential at any point of the electric dipole

1. The electric potential on the axis of the electric dipole:

Let us consider, An electric dipole AB made up of two charges of -q and +q coulomb is placed in a vacuum or air at a very small distance of $2l$. Let a point $P$ is on the axis of an electric dipole and place at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric potential due to dipole's charges.

So Electric potential at point $P$ due $+q$ charge of electric dipole→

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r-l}$

The electric potential at point $P$ due $-q$ charge of electric dipole→

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r+l}$

Electric potential is a scalar quantity. Hence the resultant potential $V$ at the point $P$ will be the algebraic sum of the potential $V_{+q}$ and $V_{-q}$. i.e. →

$ V=V_{+q}+V_{-q}$

Now substitute the value of $V_{+q}$ and $V_{-q}$ in the above equation →

$ V= \frac{1}{4\pi \epsilon_{0}} \frac{q}{r-l} -\frac{1}{4\pi \epsilon_{0}} \frac{q}{r+l}$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{q}{r-l} - \frac{q}{r+l} \right]$

$ V= \frac{q}{4\pi \epsilon_{0}} \left[ \frac{1}{r-l} - \frac{1}{r+l} \right]$

$ V= \frac{q}{4\pi \epsilon_{0}} \left[ \frac{ \left( r+l \right)-\left (r-l \right)}{r^{2}-l^{2}} \right]$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{2ql}{r^{2}-l^{2}} \right]$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{p}{r^{2}-l^{2}} \right] \qquad \left( \because p=2ql\right)$

If $r$ is much larger then $2l$. So $l^{2}$ can be neglected in comparison to $r^{2}$. Therefore electric potential at the point $P$ due to the electric dipole is →

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{p}{r^{2}} \right] $

2. The electric potential on the equatorial line of the electric dipole:

Let us consider, An electric dipole AB made up of two charges of $+q$ and $-q$ coulomb are placed in vacuum or air at a very small distance of $2l$. Let a point $P$ be on the equatorial line of an electric dipole and place it at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric potential due to dipole's charges.

So Electric potential at point $P$ due $+q$ charge of electric dipole→

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{BP}$

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}$

The electric potential at point $P$ due $-q$ charge of electric dipole→

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{AP}$

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}$

$\therefore$ The resultant potential at point $P$ is

$ V=V_{+q}+V_{-q}$

$ V=\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}-\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}} $

$V=0 $

Thus, the electric potential is zero on the equatorial line of a dipole (but the intensity is not zero). So No work is done in moving a charge along this line.

3. The electric potential at any point of the electric dipole:

Let us consider, an electric dipole $AB$ of length $2l$ consisting of the charge $+q$ and $-q$. Let's take a point $P$ in general and its distance is $r$ from the center point $O$ of the electric dipole AB.

Let the distance of point $P$ from the point $A$ and Point $B$ of the dipole is $PB=r_{1}$ and $PA=r_{2}$ respectively.

So, The electric potential at point $P$ due to the $+q$ charge of the electric dipole is →

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{1}}$

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{2}}$

The resultant potential at point $P$ is the algebraic sum of potential due to charges $+q$ and $-q$ of the dipole. That is

$ V=V_{+q}+V_{-q}$

$ V=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{1}}-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{2}}$

$ V=\frac{1}{4\pi \epsilon_{0}} \left(\frac{q}{r_{1}}-\frac{q}{r_{2}} \right) \qquad(1)$        

Now simplify the above equation by applying the Geometry from the figure. i.e. From the figure, Acute angle $\angle POB$, we can write as,

$ r^{2}_{1}=r^{2}+l^{2}-2rlcos\theta \qquad(2)$

$ r^{2}_{2}=r^{2}+l^{2}-2rlcos \left(\pi - \theta \right)$

$ r^{2}_{2}=r^{2}+l^{2}+2rlcos \theta \qquad(3)$

The equation $(2)$ may be expressed as →

$ r^{2}_{1}=r^{2} \left[1+ \frac{l^{2}}{r^{2}}-\frac{2l}{r}cos\theta \right] $

Taking distance $r$ much greater than the length of dipole (i.e. r>>l), so we may retain only first order term in $\frac{l}{r}$,

$ \therefore r^{2}_{1}=r^{2} \left[1- \frac{2l}{r}cos\theta \right]$

$ r_{1}=r \left[1- \frac{2l}{r}cos\theta \right]^{\frac{1}{2}}$

$ \frac {1}{r_{1}}=\frac{1}{r} \left[1- \frac{2l}{r}cos\theta \right]^{-\frac{1}{2}}$

Now applying the binomial theorem in the above equation. So we get $ \frac {1}{r_{1}}=\frac{1}{r} \left[1+ \frac{l}{r}cos\theta \right]$

Similarly,

$ \frac {1}{r_{2}}=\frac{1}{r} \left[1- \frac{l}{r}cos\theta \right]$

Substituting these values in equation $(1)$, we get

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{q}{r} \left(1+ \frac{l}{r}cos\theta \right)-\frac{q}{r} \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \left(1+ \frac{l}{r}cos\theta \right)- \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \left(1+ \frac{l}{r}cos\theta \right)- \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \frac{2l cos\theta}{r}\right]$

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{2ql cos\theta}{r^{2}}\right]$

But $q\times 2l=p$ (dipole moment)

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{p cos\theta}{r^{2}}\right]$

The vector form of the above equation can be written as →

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{\overrightarrow{p} \cdot \overrightarrow{r} }{r^{2}}\right]$

The above two equations hold only under the approximation that the distance of observation point $P$ is much greater than the size of the dipole.

Special Case:   

1. At axial points $\theta=0^{\circ}$,
   
   
   then $cos\theta= cos 0^{\circ}=1$,
   
   
   Therefore, $ V=\frac{1}{4\pi\epsilon_{0}} \frac{p}{r^{2}}$
  
2. At equatorial points $\theta=90^{\circ}$,
   
   
   then $cos\theta= cos 90^{\circ}=0$,
   
   
   Therefore,$ \quad V=0$

Now comparing this result with the potential due to a point-charge, we see that:     

1. In a fixed direction, that is , fixed $\theta$, $V\propto \frac{1}{r^{2}}$. here rather than $V \propto \frac{1}{r}$;
  
2. Even for a fixed distance $r$, there is now a dependence on direction, that is, on $\theta$.

Read More

Electric field intensity due to uniformly charged plane sheet and parallel sheet

Electric field intensity due to a uniformly charged infinite plane thin sheet:

Let us consider, A plane charged sheet (It is a thin sheet so it will have surface charge distribution whether it is a conducting or nonconducting sheet) whose surface charge density is $\sigma$. From symmetry, Electric field intensity is perpendicular to the plane everywhere and the field intensity must have the same magnitude on both sides of the sheet. Let point $P_{1}$ and $P_{2}$ be the two-point on the opposite side of the sheet.

To use Gaussian law, we construct a cylindrical Gaussian surface of cross-section area $\overrightarrow{dA}$, which cuts the sheet, with points $P_{1}$ and $P_{2}$. The electric field $\overrightarrow{E}$ is normal to end faces and is away from the plane. Electric field $\overrightarrow{E}$ is parallel to cross-section area $\overrightarrow{dA}$. Therefore the curved cylindrical surface does not contribute to the flux i.e. $\oint \overrightarrow{E} \cdot \overrightarrow{dA}=0$.Hence the total flux is equal to the sum of the contribution from the two end faces. Thus, we get

$ \phi_{E}=\int_{A} \overrightarrow{E} \cdot \overrightarrow{dA}+\int_{A} \overrightarrow{E} \cdot \overrightarrow{dA}$

$ \phi_{E}= \int_{A} E \: dA \:cos 0^{\circ} +\int_{A} E \: dA \:cos 0^{\circ} $

Here the direction of $\overrightarrow{E}$ and $\overrightarrow{dA}$ is same. So the angle will be $\theta = 0^{\circ}$.

Infinite plane thin sheet

$ \phi_{E}= \int_{A} E \: dA +\int_{A} E \: dA $

$ \phi_{E}= \int_{A} 2E \: dA $

$ \phi_{E}= 2E \int_{A} \: dA $

$ \phi_{E}= 2E\:A $

$ \frac{q}{\epsilon_{0}}=2E\:A \qquad \left \{\because \phi_{E}=\frac{q}{\epsilon_{0}} \right \}$

$ E=\frac{q}{2\epsilon_{0} A}$

$\because q=\sigma A $, So the above equation can be written as:

$ E=\frac{\sigma A}{2\epsilon_{0} A} $

$ E=\frac{\sigma}{2\epsilon_{0}} $

Electric field intensity due to the uniformly charged infinite conducting plane thick sheet or Plate:

Let us consider that a large positively charged plane sheet having a finite thickness is placed in the vacuum or air. Since it is a conducting plate so the charge will be distributed uniformly on the surface of the plate. Let $\sigma$ be the surface charge density of the charge

Let's take a point $P$ close to the plate at which electric field intensity has to determine. Since there is no charge inside the conducting plate, this conducting plate can be assumed as equivalent to two plane sheets of charge i.e sheet 1 and sheet 2.

Plane Charged Plate

The magnitude of the electric field intensity $\overrightarrow {E_{1}}$ at point $P$ due to sheet 1 is →

$ E_{1}=\frac{\sigma}{2\epsilon_{0}}$    (away from sheet 1)

The magnitude of the electric field intensity $\overrightarrow {E_{2}}$ at point $P$ due to sheet 2 is →

$ E_{2}=\frac{\sigma}{2\epsilon_{0}}$    (away from sheet 2)

Since $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ are in the same direction, the magnitude of resultant intensity $\overrightarrow {E}$ at point $P$ due to both the sheet is →

$ E=E_{1}+E_{2}$

$\because \quad E=\frac{\sigma}{2\epsilon_{0}}+\frac{\sigma}{2\epsilon_{0}}$

$ E=\frac{\sigma}{\epsilon_{0}} $

The resultant electric field will be away from the plate. If the plate is negatively charged, the electric field intensity $\overrightarrow {E}$ would be directed toward the plate.

We have obtained the above formula for a 'plane' charged conductor. In fact, it holds for the electric field intensity 'just' outside a charged conductor of any shape.

Electric field intensity due to two Infinite Parallel Charged Sheets:

When both sheets are positively charged:

Let us consider, Two infinite, plane, sheets of positive charge, 1 and 2 are placed parallel to each other in the vacuum or air. Let $\sigma_{1}$ and $\sigma_{2}$ be the surface charge densities of charge on sheet 1 and 2 respectively.

Likely positive charged sheet

Let $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ be the electric field intensities at any point due to sheet 1 and sheet 2 respectively. Then,

The electric field intensity at points $P'$ →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (away from sheet 2)

Since, Electric field intensities $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ are in the same direction, the magnitude of resultant intensity at point $P'$ is given by →

$ E=E_{1}+E_{2}$

$ E=\frac{\sigma_{1}}{2 \epsilon_{0}}+\frac{\sigma_{2}}{2 \epsilon_{0}}$

$ E=\frac{1}{2 \epsilon_{0}} \left (\sigma_{1}+\sigma_{2} \right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=\frac{\sigma}{ \epsilon_{0}} $

This electric field intensity would be away from both sheet 1 and sheet 2.

The electric field intensity at points $P$→

Electric field intensity at point $P$ due to sheet 1 is →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (away from sheet 2)

Now, both electric field intensities $\overrightarrow{E_{1}}$ and $\overrightarrow{E_{2}}$ are in opposite direction. The magnitude of resultant electric field $\overrightarrow{E}$ at point $P$ is given by

$ E= E_{1}-E_{2}$

$ E=\frac{\sigma_{1}}{2 \epsilon_{0}}-\frac{\sigma_{2}}{2 \epsilon_{0}}$

$ E=\frac{1}{2 \epsilon_{0}} \left (\sigma_{1}-\sigma_{2} \right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=0 $

The electric field intensity at points $P''$ → $ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (away sheet 2)

Since, Electric field intensities $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ are in the same direction, the magnitude of resultant intensity at point $P''$ is given by →

$ E=E_{1}+E_{2}$

$ E=\frac{\sigma_{1}}{2 \epsilon_{0}}+\frac{\sigma_{2}}{2 \epsilon_{0}}$

$ E=\frac{1}{2 \epsilon_{0}} \left (\sigma_{1}+\sigma_{2} \right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=\frac{\sigma}{ \epsilon_{0}} $

This electric field intensity would be away from both sheet 1 and sheet 2.

When one-sheet is positively charged and the other sheet negatively charged:

Let us consider two sheets 1 and 2 of positive and negative charge densities $\sigma_{1}$ and $\sigma_{2}$ ($\sigma_{1} > \sigma_{2}$)

Unlike charged parallel Sheet

The electric field intensities at point $P'$ →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (toward from sheet 2)

The magnitude of the resultant electric field $E$

$ E=E_{1}-E_{2}$

$E= \frac{1}{2\epsilon_{0}} \left ( \sigma_{1}- \sigma_{2}\right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=0 $

The electric field intensities at point $P$ →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (towards sheet 2)

Since, Electric field intensities $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ are in the same direction, the magnitude of resultant intensity at point $P$ is given by →

$ E=E_{1}+E_{2}$

$ E=\frac{\sigma_{1}}{2 \epsilon_{0}}+\frac{\sigma_{2}}{2 \epsilon_{0}}$

$ E=\frac{1}{2 \epsilon_{0}} \left (\sigma_{1}+\sigma_{2} \right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=\frac{\sigma}{ \epsilon_{0}} $

The electric field intensities at point $P''$ →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (toward from sheet 2)

The magnitude of the resultant electric field $E$ →

$ E=E_{1}-E_{2}$

$E= \frac{1}{2\epsilon_{0}} \left ( \sigma_{1}- \sigma_{2}\right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=0 $

From the above expression, we can conclude that the magnitude of $E$ is free from the 'position' of the point taken in the electric field between the sheet and outside the sheet. It is also shown that the electric field between the sheet is uniform everywhere and independent of separation between the sheets.

Read More